Voici un exemple de création d'un exercice de calcul algébrique avec MathGraph.

Vous pouvez voir cette ressource en action en cliquant sur ce lien

Cet exemple est sur les puissances, mais vous pouvez faire de même pour tout autre calcul algébrique.

Vous devrez pour cela utiliser la version JavaScript de MathGraph32, version 6.4.7 ou ultérieure, ou utiliser la version en ligne sur le site de MathGraph32.

Si nécessaire, à l'aide de l'icône de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.

Commencez par créer la figure mathgraph.

Si vous désirez sauter ce qui suit vous pouvez utiliser le code Base 64 de la figure ci-dessous et, dans MathGraph32, utiliser l'icône puis choisir Figure par code Base 64.

TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcvb6#gEA#wEAAAAAAAAAAAUeAAACygAAAQEAAAAAAAAAAQAAABf#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AAVuYnZhcgABMQAAAAE#8AAAAAAAAAAAAAIA#####wAGbmJjYXMxAAE3AAAAAUAcAAAAAAAAAAAAAgD#####AAJyMQATaW50KHJhbmQoMCkqbmJjYXMxKf####8AAAACAAlDRm9uY3Rpb24C#####wAAAAEACkNPcGVyYXRpb24CAAAAAxEAAAABAAAAAAAAAAA#6+0Qnpof+P####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAACAAAAAgD#####AAFuAARyMSsyAAAABAAAAAAFAAAAAwAAAAFAAAAAAAAAAP####8AAAABAAVDRm9uYwD#####AAJlcQAHYV5uK2FebgAAAAQA#####wAAAAEACkNQdWlzc2FuY2X#####AAAAAgARQ1ZhcmlhYmxlRm9ybWVsbGUAAAAAAAAABQAAAAQAAAAHAAAACAAAAAAAAAAFAAAABAABYf####8AAAACAAZDTGF0ZXgA#####wAAAAABAAZlbm9uY2X#####EEB9cAAAAAAAQE7rhR64UewAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAE5cdGV4dHtJbCBmYXV0IMOpY3JpcmUgJEE9XEZvclNpbXB7ZXF9JCBzb3VzIGxhIGZvcm1lIGxhIHBsdXMgc2ltcGxlIHBvc3NpYmxlLn0AAAAJAP####8AAAAAAQAGZW5UZXRl#####xBAfdAAAAAAAEA7mZmZmZmaAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAOQT1cRm9yU2ltcHtlcX0AAAAGAP####8AA3JlcAAEYV4xNgAAAAcAAAAIAAAAAAAAAAFAMAAAAAAAAAABYQAAAAYA#####wADc29sAAUyKmFebgAAAAQCAAAAAUAAAAAAAAAAAAAABwAAAAgAAAAAAAAABQAAAAQAAWH#####AAAAAwAQQ1Rlc3RFcXVpdmFsZW5jZQD#####AAZyZXNvbHUAAAAJAAAACAEAAAAAAT#wAAAAAAAAAQAAAAYA#####wAEemVybwASYWJzKHgpPDAuMDAwMDAwMDAxAAAABAQAAAADAAAAAAgAAAAAAAAAAT4RLgvoJtaVAAF4AAAAAgD#####AAJuMgADMipuAAAABAIAAAABQAAAAAAAAAAAAAAFAAAABAAAAAYA#####wAGZmF1dGUxAARhXm4yAAAABwAAAAgAAAAAAAAABQAAAAwAAWEAAAAKAP####8ABWZhdXRlAAAADQAAAAgBAAAAAAE#8AAAAAAAAAEAAAAJAP####8A#wAAAQAFZmF1dGX#####FEB9KAAAAAAAQFdo9cKPXCgAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAHFcSWZ7ZmF1dGV9CnsKXHRleHR7QXR0ZW50aW9uIDogTmUgcGFzIGNvbmZvbmRyZSAkYV5cVmFse259ICsgIGFeXFZhbHtufSQgYXZlYyAkYV5cVmFse259IFx0aW1lcyBhXlxWYWx7bn0kfQp9CnsKfQAAAAYA#####wACbTEAA2FebgAAAAcAAAAIAAAAAAAAAAUAAAAEAAFhAAAACQD#####AAAA#wEACHNvbHV0aW9u#####xRAIwAAAAAAAEBC0euFHrhSAQHv7#sAAAAAAAAAAAAAAAEAAAAAAAAAAAC7XGJlZ2lue2FycmF5fXtsfQpcdGV4dHtPbiB1dGlsaXNlIGxhIHLDqGdsZSBkZSBjYWxjdWwgOiAgJHgreD0yeCQgYXZlYyAkeD1cRm9yU2ltcHttMX0kfQpcXCBcdGV4dHskQSA9IFxGb3JTaW1we3NvbH0kfQpcXCBcdGV4dHskQT1cRm9yU2ltcHtzb2x9JCDDqXRhaXQgbGEgcsOpcG9uc2UgYXR0ZW5kdWUufQpcZW5ke2FycmF5fQAAAAIA#####wACYTEACTErcmFuZCgwKQAAAAQAAAAAAT#wAAAAAAAAAAAAAxEAAAABAAAAAAAAAAA#5dEoNtrGKgAAAAIA#####wACYTIACzErMipyYW5kKDApAAAABAAAAAABP#AAAAAAAAAAAAAEAgAAAAFAAAAAAAAAAAAAAAMRAAAAAQAAAAAAAAAAP8JPDbAxcWAAAAACAP####8AAmEzAAsxKzMqcmFuZCgwKQAAAAQAAAAAAT#wAAAAAAAAAAAABAIAAAABQAgAAAAAAAAAAAADEQAAAAEAAAAAAAAAAD#HPZ1VQwjAAAAAAgD#####AAVleGFjdABBemVybyhyZXAoYTEpLXNvbChhMSkpJnplcm8ocmVwKGEyKS1zb2woYTIpKSZ6ZXJvKHJlcChhMyktc29sKGEzKSkAAAAECgAAAAQK#####wAAAAEADkNBcHBlbEZvbmN0aW9uAAAACwAAAAQBAAAACwAAAAgAAAAFAAAAEgAAAAsAAAAJAAAABQAAABIAAAALAAAACwAAAAQBAAAACwAAAAgAAAAFAAAAEwAAAAsAAAAJAAAABQAAABMAAAALAAAACwAAAAQBAAAACwAAAAgAAAAFAAAAFAAAAAsAAAAJAAAABQAAABQAAAACAP####8AB3JlcG9uc2UAGnNpKHJlc29sdSwxLHNpKGV4YWN0LDIsMCkp#####wAAAAEADUNGb25jdGlvbjNWYXIAAAAABQAAAAoAAAABP#AAAAAAAAAAAAAMAAAAAAUAAAAVAAAAAUAAAAAAAAAAAAAAAQAAAAAAAAAA################

Sinon : Cette figure doit vérifier un certain nombre de propriétés pour être adaptée à LaboMep, en particulier notre figure devra contenir un calcul nommé reponse qui vaudra

• 0 si la réponse est fausse
• 1 si la réponse de l’élève est bonne et écrite sous la forme demandée
• 2 si elle est exacte mais pas écrite sous la forme demandée

Cet exercice demandera d’écrire sous la forme la plus simple possible aⁿ + aⁿ , où n est un entier naturel.

Si la figure est bien conçue, lors d’une répétition aléatoire de l’exercice, les calculs proposés ne seront pas les mêmes.

Le nombre de paramètres aléatoires de la figure sera ici de 1 (juste la valeur de n). Pour cela notre figure devra contenir un calcul nommé nbvar contenant la valeur 1, un calcul nommé r1 chargé des tirages aléatoires et un autre calcul nbcas1 contenant le nombre de valeurs que peut prendre le calcul r1.

La figure que nous allons créer ici ne sera pas affichée (dans certains cas on peut s'appuyer sur une figure pour demander de calculer une expression, mais ça ne sera pas le cas ici.

Dans MathGraph32, utilisez l'icône de création d'une nouvelle figure et cliquez sur l'item Figure sans repère et sans longueur unité.

Créez un calcul nommé nbvar (icône dans la troisième rangée d'icônes à partir du bas réservée aux calculs) contenant comme formule 1. Ce sera le nombre de paramètres aléatoires de notre exercice.

Créez de même un nouveau calcul nommé nbcas1 avec comme formule 7.

Créez un calcul nommé r1 contenant comme formule int(rand(0)*nbcas1). Ainsi le calcul r1 pourra prendre 7 valeurs entières (de 0 à 6).

Créez un calcul nommé n contenant comme formule r1+2. Ainsi n contiendra un entier compris entre 2 et 9.

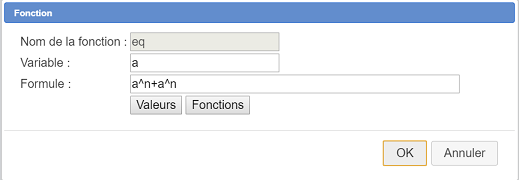
Utilisez l’icône (Troisième rangée d'icônes à partir du bas à gauche) et créez comme indiqué ci-dessous une fonction nommée eq de la variable a avec comme formule a^n + a^n.

La figure va fournir l'énoncé à afficher avant le calcul. Pour cela la figure doit contenir un affichage LaTex de tag enonce. Cet affichage LaTeX peut contenir une ou plusieurs lignes qui doivent être contenues dans des codes LaTeX \text{} successifs (pour avoir plusieurs lignes il est conseillé d'utiliser un tableau en cliquant sur l'icône lors de l'édition du code LaTeX). Ici notre consigne sera formée d'une seule ligne.

Utilisez l’icône (quatrième rangée d'icônes à partir du bas réservée aux affichages) pour créer un affichage LaTeX libre en haut et à droite de la figure avec comme code LaTeX le code ci-dessous :

\text{Il faut écrire $A=\ForSimp{eq}$ sous la forme la plus simple possible.}

.

Ce qui sera fourni à j3p pour l'affichage de l'énoncé sera donc le contenu du champ \text c'est-à-dire :

Il faut écrire $A=\ForSimp{eq}$ sous la forme la plus simple possible.

Ce qui est fourni est du LaTeX en mode texte donc, à l'intérieur de ce code, il faut encadrer de $ ce qui doit être affiché en mode maths. Le code LaTeX \ForSimp est un code LaTeX interne à MathGraph32 qui demande ici d’écrire la formule du calcul eq sous la forme la plus simple possible. On peut insérer ce code LaTeX en cliquant sur le bouton Insertion de formule.

Il nous faut maintenant donner à cet affichage LaTeX un tag (une étiquette) de valeur enonce.

L'affectation d'un tag à un élément graphique de la figure se fait via l'outil Protocole de la barre d'outils supérieure.

Une boîte de dialogue s'ouvre présentant tous les objets de la figure. En bas de la liste de gauche cliquez sur l'affichage LaTeX que nous venons de créer (lat1). Cliquez ensuite sur le bouton Changer le tag puis entrez comme tag enonce et validez. Refermez la boîte de dialogue de protocole.

Nous allons aussi fournir à la figure un autre affichage LaTeX chargé de fournir ce qui devra être affiché devant le signe = lorsque l'élève proposera ses réponses.

Utilisez de nouveau l’icône pour créer un affichage LaTeX libre au-dessous de l'affichage LaTeX précédent avec comme code LaTeX le code ci-dessous :

A=\ForSimp{eq}

.

Vous remarquerez que pour celui-ci on n'utilise pas de \text{} pour contenir ce qui doit être fourni comme en-tête (l'en-tête est fournie en mode maths). Pour que cet affichage LaTeX soit reconnu comme en-tête, il faut lui affecter le tag enTete.

Utilisez de nouveau l'outil Protocole de la barre d'outils supérieure, cliquez en bas de la liste de gauche sur le dernier élément (lat2) et affectez lui le tag enTete en cliquant sur le bouton Changer le tag.

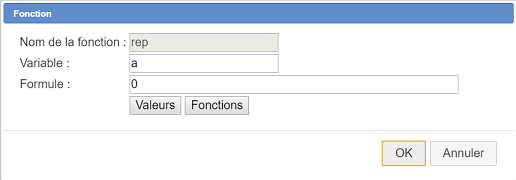
A l'aide de l'icône , Créez maintenant comme ci-dessous une fonction réelle nommée rep de la variable a avec comme formule 0. C’est cette fonction qui sera chargé de recueillir la réponse de l’élève.

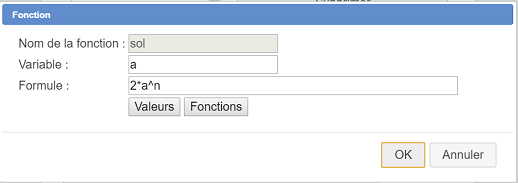
Créez une fonction réelle nommée sol contenant la formule 2*a^n que nous souhaitons voir donnée par l’élève comme ci-dessous :

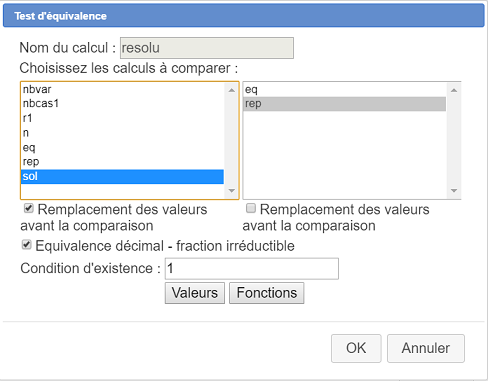
Pour savoir si la réponse de l’élève est bien la réponse souhaitée, nous allons créer un test d'équivalence. Utilisez l'icône situé à l'extrémité droite de la barre d'outils réservée aux calculs (troisième à partir du bas), cliquez sur Test d’équivalence et remplissez la boîte de dialogue comme ci-dessous. Le nom choisi pour ce test doit resolu.

Le principe est le suivant : La valeur de n est remplacée dans le calcul sol, les éventuelles multiplications par 1 et additions de 0 sont simplifiées, puis le résultat est comparé au calcul contenu dans rep (en tenant compte de la commutativité des opérations). Si les calculs sont identiques (à l’ordre des opérateurs près) resolu contiendra la valeur 1 et sinon il contiendra 0.

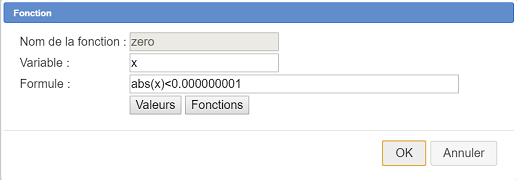
Nous devons aussi savoir si la réponse de l’élève est exacte ou fausse. Créez une nouvelle fonction réelle de la variable x définie par la formule ci-dessous :

zero(x) = abs(x)<0.000000001

MathGraph32 ne possédant pas de réel module de calcul formel nous allons tester l’égalité entre la fonction entrée par l’élève et celle donnée par la fonction eq pour trois valeurs aléatoires de x.

A l’aide de l’icône (calcul réel) créer trois calculs réels nommés a1, a2 et a3 avec pour chacun la formule ci-dessous :

1+rand(0)

Ces trois calculs prendront 3 valeurs aléatoires entre 1 et 2 (2 exclu).

Créez maintenant un autre calcul réel nommé exact contenant comme formule la formule ci-dessous :

zero(rep(a1)-sol(a1))&zero(rep(a2)-sol(a2))&zero(rep(a3)-sol(a3))

Créez ensuite un autre calcul réel nommé reponse contenant comme formule

si(resolu,1,si(exact,2,0))

La syntaxe du si est si(calcul, valeursivrai, valeursifaux) : Si calcul vaut 1, le si renvoie valeursivrai et sinon il renvoie valeursifaux.

Ainsi le calcul reponse contiendra 1 si l’élève a bien donné la forme la plus simple du calcul demandé, 2 si sa réponse est exacte mais n’est pas la forme demandée et 0 si elle est fausse.

Nous voudrions maintenant qu’un message d’avertissement s’affiche si l’élève a donné une réponse correspondant à a^(2n), ce qui correspond à une confusion entre addition et multiplication. Ce message éventuel sera affiché par J3p au-dessous de la réponse de l'élève quand elle est fausse.

Créez un nouveau calcul réel nommé n2 contenant comme formule 2*n.

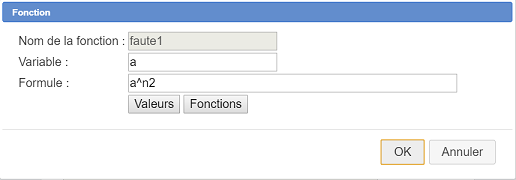
Avec l’icône créez une fonction nommée faute1 de la variable a contenant comme formule a^n2.

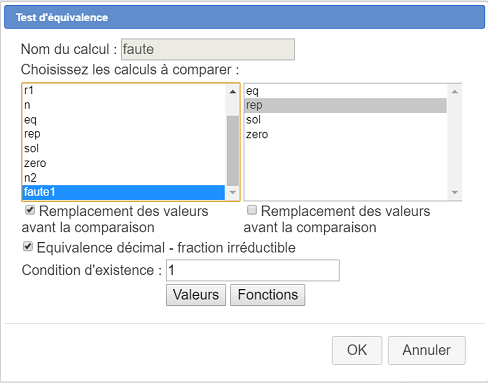
Utilisez l'icône situé à l'extrémité droite de la barre d'outils réservée aux calculs et cliquez sur Test d’équivalence et remplissez la boîte de dialogue comme ci-dessous. Nous appelrons ce test d'équivalence faute.

Le calcul faute contiendra donc 1 si l’élève a fait la confusion que nous voulons relever.

Nous allons maintenant créer une affichage LaTeX chargé de fournir ce qui doit être affiché au-dessous de la réponse de l'élève quand sa réponse est fausse et qu'il a fait la confusion entre somme et produit.

Activez l’outil de création d’un affichage LaTeX (quatrième rangée d’icônes à partir du bas) et cliquez au-dessous des affichages LaTeX précédents.

Voici le code LaTeX à utiliser :

\If{faute}
{
\text{Attention : Ne pas confondre $a^\Val{n} +  a^\Val{n}$ avec $a^\Val{n} \times a^\Val{n}$}
}
{
}

Voici comment fonctionne ce code LaTex: Il utilise un code LaTeX conditionnel \If spécifique à MathGraph32. La syntaxe est de la forme : \If{nomCalcul]{contenuLaTeX1}{ContenuLatex2} Si le calcul de nom nomCalcul a la valeur 1 alors c'est contenuLaTeX1 qui est renvoyé et sinon c'est contenuLaTeX2. Ici, donc, si le test d'équivalence vaut 1 (donc si la réponse de l'élève correspond à une confusion entre addition et multiplication) on renvoie le code LaTeX :

\text{Attention : Ne pas confondre $a^\Val{n} +  a^\Val{n}$ avec $a^\Val{n} \times a^\Val{n}$}

sinon on revoie un code LaTeX vide. Le code LaTeX renvoyé doit être entièrement contenu dans un \text{} Pour que cela fonctionne il faut donner à ce nouvel affichage LaTeX le tag faute. Pour cela utilisez l'outil comme précédemment.

Une remarque : ce dernier n'est pas visible sur la figure puique rep contient la formule 0 qui n'est pas équivalente à la formule de la fonction faute1.

Si, par exemple, le calcul affiché est A = a^8 + a^8, utilisez l'icône de la barre supérieure (modification d'objet numérique), cliquez dans la liste sur rep puis cliquez sur le bouton Modifier (vous pouvez aussi double-cliquer sur rep). Dans la boîte de dialogue qui s'ouvre, entrez comme formule pour rep : a^16 et validez (remplacez a^16 par ce qui est adapté por votre figure car le calcul a été choisi aléatoirement). Normalement l'affichage LaTex de l'erreur devrait être visible. Vous pouvez remettre 0 comme formule dans rep (ou laisser tel quel qi vous le souhaitez).

Il nous reste à créer un affichage LaTeX qui contiendra la solution expliquée pour cet exercice. Mais auparavant nous devons créer une nouvelle fonction nommée m1 qui sera utilisée dans cet affichage LaTeX.

Avec l’icône créez une fonction nommée m1 de la variable a contenant comme formule a^n.

Dans la palette des couleurs, activez la couleur bleue puis utilisez l’icône de création d’affichage LaTeX libre. Cliquez en haut et à gauche de la figure puis, dans la boîte de dialogue, entrez le code LaTeX suivant :

\begin{array}{l}
\text{On utilise la règle de calcul :  $x+x=2x$ avec $x=\ForSimp{m1}$}
\\ \text{$A = \ForSimp{sol}$}
\\ \text{$A=\ForSimp{sol}$ était la réponse attendue.}
\end{array}

Pour cet affichage LaTeX nous avons utilisé un tableau en cliquant sur l'icône qui fourni le code :

\begin{array}{l}

\\
\end{array}

Pour rajouter des lignes supplémentaires il suffit d'aller à la ligne et de commencer la nouvelle ligne par
Les lignes de ce tableau sont des \text{} dont le contenu est chaque ligne à afficher par j3p pour la correction.

Nous devons donner à cet affichage LaTeX le tag solution pour qu'il soit reconnu comme fournissant la solution de notre exercice.

Utilisez l'outil Protocole de la barre d'outils supérieure, sélectionnez cet affichage LaTeX en fin de liste et utilisez le bouton Changer le Tag pour lui affecer le tag solution.

A ce niveau votre figure doit ressembler à ceci :

A noter : Si notre figure était visible de devait faire apparaître des éléments supplémentaires lors de la correction il nous faudrait créer une macro d'intitulé solution chargé de faire apparaître ces éléments de correction. Ici ce n'est pas le cas notre figure n'est pas affichée et ne sert qu'à fournir des éléments à j3p pour qu'ils les affiche au bon moment.

Connectez vous à LaboMep V2 avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/

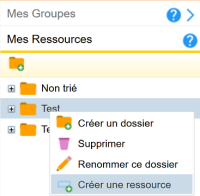
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).

Cliquez sur l’item de menu Créer une ressource.

Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.

Dans le champ Titre, entrez Puissances a^n + a^n.

Dans le champ Type technique, choisissez activité j3p.

Dans Catégories, cochez la case Exercice interactif.

Dans Niveau, cochez les cases seconde et troisième.

Dans les champs Résumé et Description, entrez Demande d’écrire a^n + a^n sous la forme la plus possible.

En bas de la page, cliquez sur Enregistrer.

Apparaît alors en bas de la page un éditeur de graphe.

Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.

Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour j3p.

Ensuite faites glisser Exercice de calcul MathGraph32 avec éditeur externe dans l’éditeur de graphe.

Un nœud apparaît (Nœud 1).

Faites un clic droit sur Nœud 1 et choisissez Paramétrage.

Dans le champ Titre entrez ce qui suit (les balises <sup>permettent d’écrire en exposant en html). <code>Calcul de aⁿ+aⁿ</code>

Le champ fig doit contenir le code Base64 de la figure que nous avons préparé.

Si nécessaire, rouvrez la figure et utilisez l'icône d'exportation de la barre d'outils supérieure et choisissez Obtenir le code Base64 de la figure. Si vous utilisez la version autonome de MathGraph32, un message vous prévient que le code Base 64 a été copié dans le presse-papier. Sinon une boîte de dialogue apparaît vous présentant ce code dans un champ d'édition dont vous devez copier le contenu dans le presse-papier.

Collez le contenu du presse-papier dans le champ fig (il s’agit d’une très grosse chaîne de caractères commençant par les caractères TWF0a). Cette chaîne a été fournie en haut de cet article.

Dans les champs width et height entrez 0 (nous n'avons pas de figure à afficher en dessous de l'éditeur, notre figure ne sert qu'à fournir consigne, correction et validation des réponses de l'élève).

Dans le champ nbrepetitions, entrez 2.

Dans le champ param, entrez n (nous avons un seul paramètre aléatoire qui est n).

Nous n'utiliserons pas le champ nomCalcul car nous avons fourni dans l'affichage LaTeX de tag enTete ce qui doit être affiché devant le signe d'égalité lorsque l'élève entre sa réponse.

Cochez la case Validation Auto. Ainsi, dans ce mode, l'élève pourra faire des calculs intermédiaires en appuyant sur la touche Entrée ou en cliquant sur le bouton OK et l'exercice sera validé dès qu'il aura rentré une des réponses acceptées comme réponses finales. Dans ce mode l'élève a droit à nbEssais calculs intermédiaires.

Dans le champ nbEssais entrez 3 au lieu de la valeur 6 : L’élève pourra donc appuyer 3 fois au maximum sur la touche Entrée pour tester ses calculs intermédiaires avant de cliquer sur OK pour valider sa réponse.

Ici le paramètre nbchances ne sera pas utilisé. Il le serait si nous avions mis le paramètre validationAuto à true. Dans ce cas l'élève fait ses calculs intermédiaires en appuyant sur la touche Entrée, et valide sa réponse finale en cliquant sur le bouton OK. Le paramètre nbchances est alors le nombre maximum de validations autorisées.

Le champ nblatex correspond à d'anciennes ressources et n'a plus à être utilisé (l'énoncé est fourni par l'affichage LaTeX de tag enonce).

Laissez le champ indicationfaute à true. Au cas où l’élève fera la confusion avec a^(2n) il aura un message d’indication.

Dans le champ charset entrez la chaîne suivante :

a()0123456789.+-/*²^

. Vous pouvez aussi utiliser :

a()\d.+-/*²^

(\d est un raccourci pour les chiffres).

Seuls les caractères de cette chaîne seront pris en compte quand l’élève entrera sa réponse.

A noter : Si vous laissez charset vide, il n'y aura pas de clavier virtuel lorsque voter exercice sera fait sur périphérique tactile.

Les champs enonceLigne1 à enonceLigne4 n'ont pas être utilisés. Ils servaient dans d'anciennes versions et sont maintenus pour compatibilité (notre énoncé est fourni par l'affichage LaTeX de tag enonce) Il vous faut choisir quelles sont les icônes de raccourci disponibles à l'élève sous l'éditeur de formule.

Cochez les cases btnPuis et btnFrac. Découchez les cases correspondant aux autres outils.

Laissez les autres champs tels quels et validez.

En bas de la page, cliquez sur le bouton Enregistrer.

Si vous voulez maintenant tester votre ressource, fermez d’abord l’onglet Puissances a^n + a^n puis, dans Mes Ressources, faites un clic droit sur la ressource Puissances a^n + a^n et choisissez Tester la ressource.

Vous pouvez maintenant tester la ressource : Un exercice de calcul de a^n + a^n doit vous être proposé deux fois de suite avec des valeurs différentes de n.

Vérifiez qu’au cas où l’élève fait la confusion avec a^(2n) il a bien le message rouge que nous avons prévu.

Remarque : Un tel exercice n’a d’intérêt que dans un graphe proposant des calculs divers sur les puissances. Des graphes de ce type sont déjà présents dans LaboMepV2 dans Ressources J3P – Lycée - Seconde – Numérique – Calculs algébriques – Puissances (trois niveaux). Cet exemple n’avait d’intérêt que de vous faire comprendre comment créer vos propres ressources.