Table des matières
Dérivée et tableau de variations
Nous désirons créer une ressource de calcul demandant d'abord de calculer la dérivée d'une fonction, puis de justifier son signe et enfin de dresser son tableau des variations : https://bibliotheque.sesamath.net/public/voir/64994d5c18b6dd1f03c7fd06
Pour créer cette ressource vous pouvez utiliser MathGraph32 dans sa version en ligne.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
Etape 1 : Création de la figure MathGraph
Commencez par créer la figure mathgraph.
Si vous désirez sauter ce qui suit vous pouvez utiliser le code Base 64 de la figure ci-dessous et, dans MathGraph32, utiliser l'icône ![]() puis choisir Figure par code Base 64.
puis choisir Figure par code Base 64.
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcvb6#gEA#wEAAAAAAAAAAAUeAAACygAAAQEAAAACAAAABgAXUHJlcGFyYXRpb25NdWx0aUV0YXBlczMAqkFqb3V0ZSAzIG1hY3JvcyBub21tw6llcyBtYWNyb0V0YXBlMSDDoCBtYWNyb0V0YXBlMyBhZmZlY3RhbnQgw6AgbGEgdmFyaWFibGUgZXRhcGUgbGVzIHZhbGV1cnMgZGUgMSDDoCAzLgoKIzE6VW5lIHZhcmlhYmxlIGV0YXBlIHF1aSBqb3VlcmEgbGUgbm9tYnJlIGQnaW5kaWNlIGRlIGwnw6l0YXBlAAAAAQAAAAMCAAAABP####8AAAABABFDRWxlbWVudEdlbmVyaXF1ZQAFZXRhcGX#####AAAAAP####8AAAABAB9DTWFjcm9BZmZlY3RhdGlvblZhbGV1clZhcmlhYmxlAf####8AAAD#AQAA#####xBAfuAAAAAAAEA11wo9cKPYAgAAAAAAAAAAAP####8AAAABAApDQ29uc3RhbnRlAAAAAAAAAAAAC21hY3JvRXRhcGUxAAAAAAACP#AAAAAAAAAAAAAAAAAAAQH#####AAAA#wEAAP####8QQIMoAAAAAABANdcKPXCj2AIAAAAAAAAAAAAAAAACAAAAAAAAAAAAC21hY3JvRXRhcGUyAAAAAAACQAAAAAAAAAAAAAAAAAAAAQH#####AAAA#wEAAP####8QQIbYAAAAAABANdcKPXCj2AIAAAAAAAAAAAAAAAACAAAAAAAAAAAAC21hY3JvRXRhcGUzAAAAAAACQAgAAAAAAAAAAAAAAAAABgAhVGFibGVhdVZhckF2ZWNEZXJpdjFWYWxldXJzRXRhcGUzBE5DcsOpZSB1biB0YWJsZWF1IGRlIHZhcmlhdGlvbnMgYXZlYyBkw6lyaXbDqWUgZXQgdW5lIHZhbGV1ciDDoCBtZXR0cmUgZGFucyBsYSBsaWduZSBzdXDDqXJpZXVyZSBwb3VyIHVuZSDDqXRhcGUgMyBkJ3VuIGV4ZXJjaWNlIG11bHRpIMOpdGFwZXMuCkxlIHNldWwgb2JqZXQgc291cmNlIGdyYXBoaXF1ZSBlc3QgbGUgcG9pbnQgc3Vww6lyaWV1ciBnYXVjaGUgZHUgdGFibGVhdS4KTGVzIG9iamV0cyBzb3VyY2VzIG51bcOpcmlxdWVzIHNvbnQgOgpVbiBjYWxjdWwgb3UgdmFyaWFibGUgdGFibGVhdSBkb250IGxhIHNldWxlIHV0aWxpdMOpIGVzdCBkZSBjcsOpZXIgbGVzIG9iamV0cyBmaW5hdXggbnVtw6lyaXF1ZXMuClVuIGNhbGN1bCBvdSB2YXJpYWJsZSBjb3JyZWN0aW9uIHZhbGFudCAxIHNpIGxlcyBmbMOoY2hlcyBkZSBjb3JyZWN0aW9uIGR1IHNlbnMgZGUgdmFyaWF0aW9uIGRvaXZlbnQgw6p0cmUgYWZmaWNow6llcyBldCAwIHNpbm9uLgpEZXV4IGNhbGN1bHMgcmVzZmxlY2hlMSwgcmVzZmxlY2hlMiB2YWxhbnQgMSBzaSBsYSBmbMOoY2hlIGNvcnJlc3BvbmRhbnRlIG1vbnRlLCAwIHNpIGVsbGUgZXN0IGhvcml6b250YWxlIG91IC0xIHNpIGVsbGUgZGVzY2VuZC4KRGFucyBsZXMgb2JqZXRzIGZpbmF1eCwgZGV1eCBjYWxjdWxzIGZsZWNoZTFldCBmbGVjaGUyIGRvbm5lbnQgbCfDqXRhdCBkZSBsYSBmbMOoY2hlIGNvcnJlc3BvbmRhbnRlLgojMTpjYWxjdWwgb3UgdmFyaWFibGUgc2VydmFudCDDoCBjcsOpZXIgbGVzIG9iamV0cyBmaW5hdXggbnVtw6lyaXF1ZXMuCiMyOiBjYWxjdWwgb3UgdmFyaWFibGUgdmFsYW50IDEgc2kgbGVzIGZsw6hjaGVzIGRlIGNvcnJlY3Rpb24gZG9pdmVudCDDqnRyZSBhZmZpY2jDqWVzIG91IG5vbi4KIzM6IGNhbGN1bCBkb25uYW50IGxlIHLDqXN1bHRhdCBxdWUgZG9pdCBhdm9pciBsYSBwcmVtacOocmUgZmzDqGNoZSAoLTEsIDAgb3UgMSkuCiM0OiBjYWxjdWwgZG9ubmFudCBsZSByw6lzdWx0YXQgcXVlIGRvaXQgYXZvaXIgbGEgZGV1eGnDqG1lIGZsw6hjaGUgKC0xLCAwIG91IDEpLgojNTogcG9pbnQgZG9ubmFudCBsJ2V4dHLDqW1pdMOpIGhhdXQgZXQgZ2F1Y2hlIGR1IHRhYmxlYXUuAAAABQAAAD8BAAAAgAAAAAAAB3RhYmxlYXX#####AAAAAQAAAAAACmNvcnJlY3Rpb27#####AAAAAQAAAAAACnJlc2ZsZWNoZTH#####AAAAAQAAAAAACnJlc2ZsZWNoZTL#####AAAAAQAAAAAAAAAAAAD##########wAAAAEAB0NDYWxjdWwB#####wANZXRhcGVJbnRlcm5lMwALMSswKnRhYmxlYXX#####AAAAAQAKQ09wZXJhdGlvbgAAAAACP#AAAAAAAAAAAAAEAgAAAAIAAAAAAAAAAP####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAAA#####wAAAAEAFENEcm9pdGVEaXJlY3Rpb25GaXhlAP####8BAAAAARAAAAEAAAABAAAABAE#8AAAAAAAAP####8AAAABAA9DUG9pbnRMaWVEcm9pdGUA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAUBCgAAAAAAAAAAABgAAAAcB#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAUBWwAAAAAAAAAAABv####8AAAABAAxDVHJhbnNsYXRpb24A#####wAAAAQAAAAH#####wAAAAEAC0NQb2ludEltYWdlAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAgAAAAJ#####wAAAAEADUNEZW1pRHJvaXRlT0EA#####wEAAAAAEAAAAQAAAAEAAAAIAAAACgAAAAcB#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAUAiG6z5FMG7AAAACwAAAAYA#####wEAAAABEAAAAQAAAAEAAAAEAD#wAAAAAAAAAAAABwD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABQEEAAAAAAAAAAAANAAAABwH#####AAAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABQEeAAAAAAAAAAAANAAAACAD#####AAAABAAAAA4AAAAJAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAA8AAAAQAAAACgD#####AQAAAAAQAAABAAAAAQAAAA8AAAARAAAABwH#####AAAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABP#jw8PDw8PEAAAASAAAACQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAATAAAAEAAAAAoA#####wEAAAAAEAAAAQAAAAEAAAATAAAAFAAAAAcB#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAUAF4eHh4eHiAAAAFQAAAAgA#####wAAAAQAAAAMAAAACQH#####AAAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAWAAAAFwAAAAgA#####wAAAAQAAAAPAAAACQH#####AAAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAIAAAAGQAAAAkB#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAADAAAABkAAAAIAP####8AAAAPAAAAEwAAAAkB#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAGgAAABwAAAAJAf####8AAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAABsAAAAcAAAACAD#####AAAAEwAAABYAAAAJAf####8AAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAB0AAAAf#####wAAAAEACENTZWdtZW50Af####8AAAAAABAAAAEAAAABAAAABAAAAAwAAAALAf####8AAAAAABAAAAEAAAABAAAAFgAAABgAAAALAf####8AAAAAABAAAAEAAAABAAAABAAAABYAAAALAf####8AAAAAABAAAAEAAAABAAAACAAAACAAAAALAf####8AAAAAABAAAAEAAAABAAAADAAAABgAAAALAf####8AAAAAABAAAAEAAAABAAAADwAAABsAAAALAf####8AAAAAABAAAAEAAAABAAAAEwAAAB7#####AAAAAQALQ0hvbW90aGV0aWUA#####wAAABoAAAAEAwAAAAI#8AAAAAAAAAAAAAJAAAAAAAAAAAAAAAkB#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAGwAAACgAAAAJAf####8AAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACkAAAAcAAAACQH#####AAAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAqAAAAH#####8AAAABAAdDTWlsaWV1AP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAA8AAAAIAAAADQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAATAAAAGgAAAA0A#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAFgAAAB0AAAANAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAB0AAAApAAAADQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAqAAAAGwAAAA0A#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAKgAAACkAAAANAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACsAAAAq#####wAAAAIABkNMYXRleAH#####AAAAAABAEAAAAAAAAMAYAAAAAAAAAAAAAAAaEAAAAAAAAAAAAAIAAAACAAAAAAAAAAAABy1caW5mdHkAAAAOAf####8AAAAAAMAYAAAAAAAAwAgAAAAAAAAAAAAAABsQAAAAAAACAAAAAgAAAAIAAAAAAAAAAAAHK1xpbmZ0eQAAAA4B#####wAAAAABAAAAAAAsEAAAAAAAAQAAAAEAAAACAAAAAAAAAAAABWV4cHIxAAAADgH#####AAAAAAEAAAAAAC0QAAAAAAABAAAAAQAAAAIAAAAAAAAAAAAFZXhwcjIAAAAOAf####8AAAAAAQAAAAAALhAAAAAAAAEAAAABAAAAAgAAAAAAAAAAAAVleHByMwAAAA4B#####wAAAAAAQAAAAAAAAADACAAAAAAAAAAPZm9ybXVsYWlyZUludDMxAAAAKRAAAAAAAAEAAAACAAAAAgAAAAAAAAAAAAxcdGV4dHtlZGl0MX0AAAAOAf####8A#wAAAL#wAAAAAAAAwDwAAAAAAAAACXNvbEludDMxMQAAACkQAAAAAAABAAAAAgAAAAIAAAAAAAAAAAABMQAAAA4B#####wAAAAABAA9mb3JtdWxhaXJlSW50MzIAAAAvGgAAAAAAAQAAAAEAAAACAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAAA4B#####wD#AAAAwDsAAAAAAAAAAAAAAAAAAAAKbGlzdEludDMyMQAAAC8MAAAAAAACAAAAAQAAAAIAAAAAAAAAAAA+XGJlZ2lue2FycmF5fXtsfQpcdGV4dHsrfSAKXFwgXHRleHR7LX0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAAOAf####8AAAAAAQAPZm9ybXVsYWlyZUludDMzAAAAMRoAAAAAAAEAAAABAAAAAgAAAAAAAAAAAAxcdGV4dHtsaXN0MX0AAAAOAf####8A#wAAAMA5AAAAAAAAAAAAAAAAAAAACmxpc3RJbnQzMzEAAAAxDAAAAAAAAgAAAAEAAAACAAAAAAAAAAAAP1xiZWdpbnthcnJheX17bH0KXHRleHR7fH0gClxcIFx0ZXh0e3x8fQpcXCBcdGV4dHswfQpcZW5ke2FycmF5fQAAAA4B#####wAAAAABAA9mb3JtdWxhaXJlSW50MzQAAAAwGgAAAAAAAQAAAAEAAAACAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAAA4B#####wD#AAAAwDgAAAAAAAA#8AAAAAAAAAAKbGlzdEludDM0MQAAADAMAAAAAAACAAAAAQAAAAIAAAAAAAAAAAA+XGJlZ2lue2FycmF5fXtsfQpcdGV4dHsrfSAKXFwgXHRleHR7LX0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAAOAf####8AAAAAAQAPZm9ybXVsYWlyZUludDM1AAAAMhAAAf###wAAAAEAAAABAAAAAgAAAAAAAAAAAAxcdGV4dHtlZGl0MX0AAAAOAf####8A#wAAAAAAAAAAAAAAwCIAAAAAAAAACXNvbEludDM1MQAAADIQAAH###8AAAABAAAAAgAAAAIAAAAAAAAAAAABMgAAAA0A#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAIAAAACoAAAALAP####8BAAAAABAAAAEAAAEBAAAAIAAAACoAAAAHAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAABAAE#6UEWGP+I9wAAAEMAAAAGAP####8BAAAAABAAAAEAAAEBAAAAQgE#8AAAAAAAAP####8AAAABAA9DU3ltZXRyaWVBeGlhbGUA#####wAAAEUAAAAJAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEQAAABGAAAAAwD#####AAVtaW5pMQACLTH#####AAAAAQAMQ01vaW5zVW5haXJlAAAAAj#wAAAAAAAAAAAAAwD#####AAVtYXhpMQABMQAAAAI#8AAAAAAAAAAAAAMA#####wAEcGFzMQABMQAAAAI#8AAAAAAAAP####8AAAABAAtDUG9pbnRDbG9uZQD#####AQAAAAALAAJPMQDAOAAAAAAAAD#wAAAAAAAAAAABAAAAAEcAAAAMAP####8AAABLAAAABAMAAAAFAAAASgAAAAQBAAAABQAAAEkAAAAFAAAASP####8AAAABAA5DUG9pbnRMaWVQb2ludAD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABEAAAACwD#####AQAAAAAQAAABAAABAQAAAEsAAABN#####wAAAAEAFkNEcm9pdGVQZXJwZW5kaWN1bGFpcmUA#####wEAAAAAEAAAAQAAAAEAAABLAAAATgAAAAcA#####wEAAAAACwACSjEAwDYAAAAAAADALgAAAAAAAAAAAQABv74ZFMew#VkAAABPAAAACQD#####AQAAAAALAAJJMQAAAAAAAAAAAEAAAAAAAAAAAAABAAAAAE0AAABM#####wAAAAIAB0NSZXBlcmUB#####wAAAAAAAAEBAAAASwAAAFEAAABQAAAAAAAABQAAAEgAAAACAAAAAAAAAAAAAAAFAAAASgAAAAI#8AAAAAAAAP####8AAAABAA1DUG9pbnRCYXNlRW50Af####8A#wAAARAAAlQxAAAAAAAAAAAAQAgAAAAAAAAAAAgAAQAAAFI#8AAAAAAAAAAAAAAAAAAAAAAAAAAFAAAASAAAAAUAAABJAAAAAgAAAAAAAAAAAAAAAgAAAAAAAAAA#####wAAAAIACENNZXN1cmVYAf####8ABm1lc2FicwAAAFIAAABTAAAAAwH#####AAdmbGVjaGUxACVpbnQobWVzYWJzKjEwMDAwMDAwMDArMC41KS8xMDAwMDAwMDAwAAAABAP#####AAAAAgAJQ0ZvbmN0aW9uAgAAAAQAAAAABAIAAAAFAAAAVAAAAAJBzc1lAAAAAAAAAAI#4AAAAAAAAAAAAAJBzc1lAAAAAP####8AAAABABFDU3ltZXRyaWVDZW50cmFsZQD#####AAAAQgAAAAkB#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAUwAAAFb#####AAAAAQAIQ1ZlY3RldXIB#####wAAAAAAEAAAAQAAAAIAAABXAAAAUwAAAAAMAP####8AAABRAAAABAMAAAAFAAAAAgAAAAQKAAAABQAAAAEAAAAECQAAAAUAAABVAAAABQAAAAIAAAAJAf####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAE0AAABZAAAACQH#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABaAAAAVgAAABkB#####wD#AAAAEAAAAQAAAAIAAABbAAAAWgAAAAANAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACsAAAAeAAAACwD#####AQAAAAAQAAABAAABAQAAACsAAAAeAAAABwD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAAAQABP+lBFhj#iPcAAABeAAAABgD#####AQAAAAAQAAABAAABAQAAAF0BP#AAAAAAAAAAAAAPAP####8AAABgAAAACQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABfAAAAYQAAAAMA#####wAGbWluaTExAAItMQAAABAAAAACP#AAAAAAAAAAAAADAP####8ABm1heGkxMQABMQAAAAI#8AAAAAAAAAAAAAMA#####wAFcGFzMTEAATEAAAACP#AAAAAAAAAAAAARAP####8BAAAAAAsAAU8AwDgAAAAAAAA#8AAAAAAAAAAAAQAAAABiAAAADAD#####AAAAZgAAAAQDAAAABQAAAGUAAAAEAQAAAAUAAABkAAAABQAAAGMAAAASAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAF8AAAALAP####8BAAAAABAAAAEAAAEBAAAAZgAAAGgAAAATAP####8BAAAAABAAAAEAAAABAAAAZgAAAGkAAAAHAP####8BAAAAAAsAAUoAwDYAAAAAAADALgAAAAAAAAAAAQABv74ZFMew#VkAAABqAAAACQD#####AQAAAAALAAFJAAAAAAAAAAAAQAAAAAAAAAAAAAEAAAAAaAAAAGcAAAAUAf####8AAAAAAAABAQAAAGYAAABsAAAAawAAAAAAAAUAAABjAAAAAgAAAAAAAAAAAAAABQAAAGUAAAACP#AAAAAAAAAAAAAVAf####8A#wAAARAAAVQAAAAAAAAAAABACAAAAAAAAAAACAABAAAAbT#wAAAAAAAAAAAAAAAAAAAAAAAAAAUAAABjAAAABQAAAGQAAAACAAAAAAAAAAAAAAACAAAAAAAAAAAAAAAWAf####8AB21lc2FiczEAAABtAAAAbgAAAAMB#####wAHZmxlY2hlMgAmaW50KG1lc2FiczEqMTAwMDAwMDAwMCswLjUpLzEwMDAwMDAwMDAAAAAEAwAAABcCAAAABAAAAAAEAgAAAAUAAABvAAAAAkHNzWUAAAAAAAAAAj#gAAAAAAAAAAAAAkHNzWUAAAAAAAAAGAD#####AAAAXQAAAAkB#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAbgAAAHEAAAAZAf####8AAAAAABAAAAEAAAACAAAAcgAAAG4AAAAADAD#####AAAAbAAAAAQDAAAABQAAAAMAAAAECgAAAAUAAAABAAAABAkAAAAFAAAAcAAAAAUAAAADAAAACQH#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABoAAAAdAAAAAkB#####wD#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAdQAAAHEAAAAZAf####8A#wAAABAAAAEAAAACAAAAdgAAAHUAAAAAAwH#####AAlyZXBJbnQzMTEAB3RhYmxlYXUAAAAFAAAAAAAAAAMB#####wAMcmVzb2x1SW50MzExAAd0YWJsZWF1AAAABQAAAAAAAAADAf####8ADXJlc0xpc3RJbnQzMjEAB3RhYmxlYXUAAAAFAAAAAAAAAAMB#####wANcmVzTGlzdEludDMyMwAHdGFibGVhdQAAAAUAAAAAAAAAAwH#####AA1yZXNMaXN0SW50MzI0AAd0YWJsZWF1AAAABQAAAAAAAAADAf####8ACXJlcEludDM1MQAHdGFibGVhdQAAAAUAAAAAAAAAAwH#####AAxyZXNvbHVJbnQzNTEAB3RhYmxlYXUAAAAFAAAAAAAAAAMB#####wAHcmVzb2x1MwAlZmxlY2hlMT1yZXNmbGVjaGUxJmZsZWNoZTI9cmVzZmxlY2hlMgAAAAQKAAAABAgAAAAFAAAAVQAAAAUAAAACAAAABAgAAAAFAAAAcAAAAAUAAAADAAAAAQAAAMb#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0NgAAAAJACSH7VEQtGP####8AAAABAA9DVmFyaWFibGVCb3JuZWUA#####wAFZXRhcGU#8AAAAAAAAD#wAAAAAAAAQAgAAAAAAAA#8AAAAAAAAAAAATEAATMAATEAAAAbAP####8ACmNvcnJlY3Rpb24AAAAAAAAAAAAAAAAAAAAAP#AAAAAAAAA#8AAAAAAAAAAAATAAATEAATH#####AAAAAQAIQ01hdHJpY2UA#####wAFbWF0YWIAAAAKAAAAAgAAAAI#8AAAAAAAAAAAAAJAAAAAAAAAAAAAAAI#8AAAAAAAAAAAAAJACAAAAAAAAAAAAAJAAAAAAAAAAAAAAAI#8AAAAAAAAAAAAAJAAAAAAAAAAAAAAAJACAAAAAAAAAAAAAJAAAAAAAAAAAAAAAJAFAAAAAAAAAAAAAJACAAAAAAAAAAAAAI#8AAAAAAAAAAAAAJACAAAAAAAAAAAAAJAAAAAAAAAAAAAAAJACAAAAAAAAAAAAAJAEAAAAAAAAAAAAAJAEAAAAAAAAAAAAAI#8AAAAAAAAAAAAAJAEAAAAAAAAAAAAAJACAAAAAAAAAAAAAMA#####wAIbmJFdGFwZXMAATMAAAACQAgAAAAAAAAAAAADAP####8ABW5idmFyAAEyAAAAAkAAAAAAAAAAAAAAAwD#####AAZuYmNhczEADG5icm93KG1hdGFiKf####8AAAACAAxDRm9uY3Rpb25NYXQbAAAABQAAAAMAAAADAP####8ABm5iY2FzMgABMgAAAAJAAAAAAAAAAAAAAAMA#####wACcjEAE2ludChyYW5kKDApKm5iY2FzMSkAAAAXAgAAAAQCAAAAFxEAAAACAAAAAAAAAAA#7xmalM1sAgAAAAUAAAAGAAAAAwD#####AAJyMgATaW50KHJhbmQoMCkqbmJjYXMyKQAAABcCAAAABAIAAAAXEQAAAAIAAAAAAAAAAD#ekxEDC2mcAAAABQAAAAcAAAADAP####8AE2ZpZ3VyZU1hc3F1ZWVFdGFwZTEAATEAAAACP#AAAAAAAAAAAAADAP####8AE2ZpZ3VyZU1hc3F1ZWVFdGFwZTIAATEAAAACP#AAAAAAAAAAAAADAP####8AAngxAAwxK3JhbmQoMCkvMTAAAAAEAAAAAAI#8AAAAAAAAAAAAAQDAAAAFxEAAAACAAAAAAAAAAA#y6djtc4WmAAAAAJAJAAAAAAAAAAAAAMA#####wACeDIADjEuMStyYW5kKDApLzEwAAAABAAAAAACP#GZmZmZmZoAAAAEAwAAABcRAAAAAgAAAAAAAAAAP95MYJoZk8AAAAACQCQAAAAAAAAAAAADAP####8AAngzAA4xLjIrcmFuZCgwKS8xMAAAAAQAAAAAAj#zMzMzMzMzAAAABAMAAAAXEQAAAAIAAAAAAAAAAD#m5GV+VxJ0AAAAAkAkAAAAAAAAAAAAAwD#####AARhYnNhAA1tYXRhYihyMSsxLDEp#####wAAAAEACENUZXJtTWF0AAAAAwAAAAQAAAAABQAAAAgAAAACP#AAAAAAAAAAAAACP#AAAAAAAAAAAAADAP####8AAWIADW1hdGFiKHIxKzEsMikAAAAeAAAAAwAAAAQAAAAABQAAAAgAAAACP#AAAAAAAAAAAAACQAAAAAAAAAAAAAADAP####8AAWEADCgtMSlecjIqYWJzYQAAAAQC#####wAAAAEACkNQdWlzc2FuY2UAAAAQAAAAAj#wAAAAAAAAAAAABQAAAAkAAAAFAAAADwAAAAMA#####wADZ2FiABNwZ2NkKGFicyhhKSxhYnMoYikp#####wAAAAEADUNGb25jdGlvbjJWYXICAAAAFwAAAAAFAAAAEQAAABcAAAAABQAAABAAAAADAP####8AAmEnAAVhL2dhYgAAAAQDAAAABQAAABEAAAAFAAAAEgAAAAMA#####wACYjEACmFicyhiKS9nYWIAAAAEAwAAABcAAAAABQAAABAAAAAFAAAAEgAAAAMA#####wACYicAFnNpKGEnPjAmYSc9YjEsYScrMSxiMSn#####AAAAAQANQ0ZvbmN0aW9uM1ZhcgAAAAAECgAAAAQFAAAABQAAABMAAAACAAAAAAAAAAAAAAAECAAAAAUAAAATAAAABQAAABQAAAAEAAAAAAUAAAATAAAAAj#wAAAAAAAAAAAABQAAABQAAAADAP####8AAWUABmV4cCgxKQAAABcHAAAAAj#wAAAAAAAAAAAAAwD#####AARhcG9zAARhJz4wAAAABAUAAAAFAAAAEwAAAAIAAAAAAAAAAAAAAAMA#####wADYW1iAAVhJy1iJwAAAAQBAAAABQAAABMAAAAFAAAAFQAAAAMA#####wACeDAABmFtYi9hJwAAAAQDAAAABQAAABgAAAAFAAAAEwAAAAMA#####wAIeHplcm9wb3MABHgwPjAAAAAEBQAAAAUAAAAZAAAAAgAAAAAAAAAA#####wAAAAEACUNGb25jTlZhcgD#####AAFmABAoYScqeCtiJykqZV4oLXgpAAAABAIAAAAEAAAAAAQCAAAABQAAABP#####AAAAAgARQ1ZhcmlhYmxlRm9ybWVsbGUAAAABAAAABQAAABUAAAAfAAAAIwAAAAAAAAAQAAAAIwAAAAEAAAACAAFlAAF4AAAAIgD#####AAZzb2xmJzEAEigtYScqeCthbWIpKmVeKC14KQAAAAQCAAAABAAAAAAQAAAABAIAAAAFAAAAEwAAACMAAAABAAAABQAAABgAAAAfAAAAIwAAAAAAAAAQAAAAIwAAAAEAAAACAAFlAAF4AAAAIgD#####AAZzb2xmJzIADygtYScqeCthbWIpL2VeeAAAAAQDAAAABAAAAAAQAAAABAIAAAAFAAAAEwAAACMAAAABAAAABQAAABgAAAAfAAAAIwAAAAAAAAAjAAAAAQAAAAIAAWUAAXgAAAAiAP####8ABnNvbGYnMwASLShhJyp4LWFtYikqZV4oLXgpAAAAEAAAAAQCAAAABAEAAAAEAgAAAAUAAAATAAAAIwAAAAEAAAAFAAAAGAAAAB8AAAAjAAAAAAAAABAAAAAjAAAAAQAAAAIAAWUAAXgAAAAiAP####8ABnNvbGYnNAAPLShhJyp4LWFtYikvZV54AAAAEAAAAAQDAAAABAEAAAAEAgAAAAUAAAATAAAAIwAAAAEAAAAFAAAAGAAAAB8AAAAjAAAAAAAAACMAAAABAAAAAgABZQABeAAAAAEA#####wAAAP8BAAD#####EECBGAAAAAAAQDXXCj1wo9gCAAAAAAAAAAAAAAAAAgAAAAAAAAAAAAttYWNyb0V0YXBlMQAAAAAAAj#wAAAAAAAAAAAAAQAAAAEA#####wAAAP8BAAD#####EECEmAAAAAAAQDXXCj1wo9gCAAAAAAAAAAAAAAAAAgAAAAAAAAAAAAttYWNyb0V0YXBlMgAAAAAAAkAAAAAAAAAAAAAAAQAAAAEA#####wAAAP8BAAD#####EECIOAAAAAAAQDXXCj1wo9gCAAAAAAAAAAAAAAAAAgAAAAAAAAAAAAttYWNyb0V0YXBlMwAAAAAAAkAIAAAAAAAAAAAAAQAAAA4A#####wAAAAABAAdlbm9uY2Ux#####xBAQAAAAAAAAEByvXCj1wo+AAAAAAAAAAAAAAAAAAQDAAAAAgAAAAAAAAAAAAAABAgAAAAFAAAAAQAAAAI#8AAAAAAAAAFPXGJlZ2lue2FycmF5fXtsfQpcdGV4dHskZiQgZXN0IGxhIGZvbmN0aW9uIGTDqWZpbmllIHN1ciAkXFIkIHBhciAkZih4KT1cRm9yU2ltcHtmfSQgZXQgJGYnJCBkw6lzaWduZSBzYSBmb25jdGlvbiBkw6lyaXbDqWUufSAKXFwgXHRleHR7JFx0ZXh0Y29sb3J7bWFyb29ufXtcdGV4dHtEYW5zIHVuIHByZW1pZXIgdGVtcHMsIG9uIGRlbWFuZGUgZGUgY2FsY3VsZXIgfWYnKHgpfSQufQpcXCBcdGV4dHtMZSByw6lzdWx0YXQgZG9pdCDDqnRyZSBkb25uw6kgc291cyB1bmUgZm9ybWUgc2ltcGxlIHBlcm1ldHRhbnQgZCfDqXR1ZGllciBsZSBzaWduZSBkZSAkZicoeCkkLn0KXGVuZHthcnJheX0AAAAOAP####8AAAAAAQALZm9ybXVsYWlyZTH#####EEBBgAAAAAAAQHi9cKPXCj4AAAAAAAAAAAAAAAAABAMAAAACAAAAAAAAAAAAAAAECAAAAAUAAAABAAAAAj#wAAAAAAAAABZcdGV4dHskZicoeCkkID0gZWRpdDF9AAAAIgD#####AAVyZXAxMQABMAAAAAIAAAAAAAAAAAAAAAIAAWUAAXj#####AAAAAwAQQ1Rlc3RFcXVpdmFsZW5jZQD#####AAl0ZXFzb2xmJzEAAAAcAAAAJQEAAAAAAj#wAAAAAAAAAQAAACQA#####wAJdGVxc29sZicyAAAAHQAAACUBAAAAAAI#8AAAAAAAAAEAAAAkAP####8ACXRlcXNvbGYnMwAAAB4AAAAlAQAAAAACP#AAAAAAAAABAAAAJAD#####AAl0ZXFzb2xmJzQAAAAfAAAAJQEAAAAAAj#wAAAAAAAAAQAAAAMA#####wAIcmVzb2x1MTEAJ3RlcXNvbGYnMXx0ZXFzb2xmJzJ8dGVxc29sZiczfHRlcXNvbGYnNAAAAAQLAAAABAsAAAAECwAAAAUAAAAmAAAABQAAACcAAAAFAAAAKAAAAAUAAAAp#####wAAAAEABUNGb25jAP####8ABHplcm8AEmFicyh4KTwwLjAwMDAwMDAwMQAAAAQEAAAAFwAAAAAjAAAAAAAAAAI+ES4L6CbWlQABeAAAAAMA#####wAHZXhhY3QxMQBcemVybyhzb2xmJzEoZSx4MSktcmVwMTEoZSx4MSkpJnplcm8oc29sZicxKGUseDIpLXJlcDExKGUseDIpKSZ6ZXJvKHNvbGYnMShlLHgzKS1yZXAxMShlLHgzKSkAAAAECgAAAAQK#####wAAAAEADkNBcHBlbEZvbmN0aW9uAAAAKwAAAAQB#####wAAAAEAEkNBcHBlbEZvbmN0aW9uTlZhcgAAAAIAAAAcAAAABQAAABYAAAAFAAAADAAAACcAAAACAAAAJQAAAAUAAAAWAAAABQAAAAwAAAAmAAAAKwAAAAQBAAAAJwAAAAIAAAAcAAAABQAAABYAAAAFAAAADQAAACcAAAACAAAAJQAAAAUAAAAWAAAABQAAAA0AAAAmAAAAKwAAAAQBAAAAJwAAAAIAAAAcAAAABQAAABYAAAAFAAAADgAAACcAAAACAAAAJQAAAAUAAAAWAAAABQAAAA4AAAAlAP####8AAXUAB2EnKngrYicAAAAEAAAAAAQCAAAABQAAABMAAAAjAAAAAAAAAAUAAAAVAAF4AAAAJQD#####AAJ1JwACYScAAAAFAAAAEwABeAAAACIA#####wABdgAGZV4oLXgpAAAAHwAAACMAAAAAAAAAEAAAACMAAAABAAAAAgABZQABeAAAACIA#####wACdicABy1lXigteCkAAAAQAAAAHwAAACMAAAAAAAAAEAAAACMAAAABAAAAAgABZQABeAAAACIA#####wAFZm9yMTEAHWEnKmVeKC14KSsoYScqeCtiJykqKC1lXigteCkpAAAABAAAAAAEAgAAAAUAAAATAAAAHwAAACMAAAAAAAAAEAAAACMAAAABAAAABAIAAAAEAAAAAAQCAAAABQAAABMAAAAjAAAAAQAAAAUAAAAVAAAAEAAAAB8AAAAjAAAAAAAAABAAAAAjAAAAAQAAAAIAAWUAAXgAAAAiAP####8ABWZvcjEyABVlXigteCkqKGEnLShhJyp4K2InKSkAAAAEAgAAAB8AAAAjAAAAAAAAABAAAAAjAAAAAQAAAAQBAAAABQAAABMAAAAEAAAAAAQCAAAABQAAABMAAAAjAAAAAQAAAAUAAAAVAAAAAgABZQABeAAAAA4A#####wAAAAABAAdlbm9uY2Uy#####xBANQAAAAAAAEBwzXCj1wo+AAAAAAAAAAAAAAAAAAQDAAAAAgAAAAAAAAAAAAAABAgAAAAFAAAAAQAAAAJAAAAAAAAAAAJ7XGJlZ2lue2FycmF5fXtsfQpcdGV4dHskZiQgZXN0IGTDqWZpbmllIHN1ciAkXFIkIHBhciAkZih4KT1cRm9yU2ltcHtmfSQufQpcXCBcdGV4dHtPbiBwZXV0IHBvc2VyICRmPXV2JCBhdmVjICR1KHgpPVxGb3JTaW1we3V9JCBldCAkdih4KT1cRm9yU2ltcHt2fSQufQpcXCBcdGV4dHskdSQgZXQgJHYkIHNvbnQgZMOpcml2YWJsZXMgc3VyICRcUiQgYXZlYyAkdScoeCk9XEZvclNpbXB7dSd9JCBldCAkdicoeCk9XEZvclNpbXB7did9JC59ClxcIFx0ZXh0eyRmJCBlc3QgZG9uYyBkw6lyaXZhYmxlIHN1ciAkXFIkIGNvbW1lIHByb2R1aXQgZGUgZGV1eCBmb25jdGlvbnMgZMOpcml2YWJsZXMgZXQgJGYnPSh1diknPXUndit1dickLn0KXFwgXHRleHR7T24gYSBkb25jICRmJyh4KT1cRm9yU2ltcHtmb3IxMX09XEZvclNpbXB7Zm9yMTJ9JH0KXFwgXHRleHR7RG9uYyAkZicoeCk9XEZvclNpbXB7c29sZicxfSQgb3UgZW5jb3JlICRmJyh4KT1cRm9yU2ltcHtzb2xmJzJ9JCBjYXIgJGVeey14fT1cZGZyYWN7MX17ZV54fSQufQpcXCBcdGV4dHskXHRleHRjb2xvcnttYXJvb259e1x0ZXh0e0NvbXBsw6l0ZXIgY2ktZGVzc291cyBkZSBsYSBmYcOnb24gbGEgcGx1cyBzaW1wbGUgcG9zc2libGUgOn19JH0KXGVuZHthcnJheX0AAAAOAP####8AAAAAAQALZm9ybXVsYWlyZTL#####EEA7AAAAAAAAQH2dcKPXCj4AAAAAAAAAAAAAAAAABAMAAAACAAAAAAAAAAAAAAAECAAAAAUAAAABAAAAAkAAAAAAAAAAAEtcdGV4dHtQb3VyIHRvdXQgcsOpZWwgJHgkLCAkZV57LXh9JCBsaXN0MSBkb25jICRmJyh4KSQgYSBsZSBzaWduZSBkZSBlZGl0MX0AAAAOAP####8A#wAAAQAGbGlzdDIx#####xBAeeAAAAAAAEB9DXCj1wo+AAAAAAAAAAAAAAAAAAQDAAAAAgAAAAAAAAAAAAAABAgAAAAFAAAAAQAAAAJAAAAAAAAAAAA0XGJlZ2lue2FycmF5fXtsfQpcdGV4dHs+MH0gClxcIFx0ZXh0ezwwfQpcZW5ke2FycmF5fQAAAAMA#####wAJcmVzTGlzdDIxAAExAAAAAj#wAAAAAAAAAAAAIgD#####AAVyZXAyMQABMAAAAAIAAAAAAAAAAAAAAAIAAWUAAXgAAAAiAP####8ABXNvbDIxAAktYScqeCthbWIAAAAEAAAAABAAAAAEAgAAAAUAAAATAAAAIwAAAAEAAAAFAAAAGAAAAAIAAWUAAXgAAAAiAP####8ABnNvbCcyMQALLShhJyp4LWFtYikAAAAQAAAABAEAAAAEAgAAAAUAAAATAAAAIwAAAAEAAAAFAAAAGAAAAAIAAWUAAXgAAAAkAP####8ACHRlcXNvbDIxAAAAOAAAADcBAAAAAAI#8AAAAAAAAAEAAAAkAP####8ACXRlcXNvbCcyMQAAADkAAAA3AQAAAAACP#AAAAAAAAABAAAAAwD#####AAhyZXNvbHUyMQASdGVxc29sMjF8dGVxc29sJzIxAAAABAsAAAAFAAAAOgAAAAUAAAA7AAAAAwD#####AAdleGFjdDIxAFl6ZXJvKHNvbDIxKGUseDEpLXJlcDIxKGUseDEpKSZ6ZXJvKHNvbDIxKGUseDIpLXJlcDIxKGUseDIpKSZ6ZXJvKHNvbDIxKGUseDMpLXJlcDIxKGUseDMpKQAAAAQKAAAABAoAAAAmAAAAKwAAAAQBAAAAJwAAAAIAAAA4AAAABQAAABYAAAAFAAAADAAAACcAAAACAAAANwAAAAUAAAAWAAAABQAAAAwAAAAmAAAAKwAAAAQBAAAAJwAAAAIAAAA4AAAABQAAABYAAAAFAAAADQAAACcAAAACAAAANwAAAAUAAAAWAAAABQAAAA0AAAAmAAAAKwAAAAQBAAAAJwAAAAIAAAA4AAAABQAAABYAAAAFAAAADgAAACcAAAACAAAANwAAAAUAAAAWAAAABQAAAA4AAAADAP####8AB3RhYmxlYXUAATEAAAACP#AAAAAAAAD#####AAAAAQAKQ1BvaW50QmFzZQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABQCYAAAAAAABAKa4UeuFHsAAAAAMA#####wAPcmVzdWx0YXRGbGVjaGUxAA1zaShhcG9zLDEsLTEpAAAAIQAAAAAFAAAAFwAAAAI#8AAAAAAAAAAAABAAAAACP#AAAAAAAAAAAAADAP####8AD3Jlc3VsdGF0RmxlY2hlMgANc2koYXBvcywtMSwxKQAAACEAAAAABQAAABcAAAAQAAAAAj#wAAAAAAAAAAAAAj#wAAAAAAAAAAAAAwD#####AA1ldGFwZUludGVybmUzAAsxKzAqdGFibGVhdQAAAAQAAAAAAj#wAAAAAAAAAAAABAIAAAACAAAAAAAAAAAAAAAFAAAAPgAAAAYA#####wEAAAABEAAAAQAAAAEAAAA#AT#wAAAAAAAAAAAABwD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABQEKAAAAAAAAAAABDAAAABwD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABQGQgAAAAAAAAAABDAAAACAD#####AAAAPwAAAEQAAAAJAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEUAAABGAAAACgD#####AQAAAAANAAABAAAAAQAAAEUAAABHAAAABwD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABQCIbrPkUwbsAAABIAAAABgD#####AQAAAAEQAAABAAAAAQAAAD8AP#AAAAAAAAAAAAAHAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAFAQQAAAAAAAAAAAEoAAAAHAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAFAR4AAAAAAAAAAAEoAAAAIAP####8AAAA#AAAASwAAAAkA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAATAAAAE0AAAAKAP####8BAAAAAA0AAAEAAAABAAAATAAAAE4AAAAHAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAE#+PDw8PDw8QAAAE8AAAAJAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFAAAABNAAAACgD#####AQAAAAANAAABAAAAAQAAAFAAAABRAAAABwD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABQAXh4eHh4eIAAABSAAAACAD#####AAAAPwAAAEkAAAAJAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFMAAABUAAAACAD#####AAAAPwAAAEwAAAAJAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEUAAABWAAAACQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABJAAAAVgAAAAgA#####wAAAEwAAABQAAAACQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABXAAAAWQAAAAkA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAWAAAAFkAAAAIAP####8AAABQAAAAUwAAAAkA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAWgAAAFwAAAALAP####8AAAAAABAAAAEAAAABAAAAPwAAAEkAAAALAP####8AAAAAABAAAAEAAAABAAAAUwAAAFUAAAALAP####8AAAAAABAAAAEAAAABAAAAPwAAAFMAAAALAP####8AAAAAABAAAAEAAAABAAAARQAAAF0AAAALAP####8AAAAAABAAAAEAAAABAAAASQAAAFUAAAALAP####8AAAAAABAAAAEAAAABAAAATAAAAFgAAAALAP####8AAAAAABAAAAEAAAABAAAAUAAAAFsAAAAMAP####8AAABXAAAABAMAAAACP#AAAAAAAAAAAAACQAAAAAAAAAAAAAAJAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFgAAABlAAAACQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABmAAAAWQAAAAkA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAZwAAAFwAAAANAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEwAAABFAAAADQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABQAAAAVwAAAA0A#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAUwAAAFoAAAANAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFoAAABmAAAADQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABnAAAAWAAAAA0A#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAZwAAAGYAAAANAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAGgAAABnAAAADgD#####AAAAAABAEAAAAAAAAMAYAAAAAAAAAAAAAABXEAAAAAAAAAAAAAIAAAACAAAAAAAAAAAABy1caW5mdHkAAAAOAP####8AAAAAAMAYAAAAAAAAwAgAAAAAAAAAAAAAAFgQAAAAAAACAAAAAgAAAAIAAAAAAAAAAAAHK1xpbmZ0eQAAAA4A#####wAAAAABAAAAAABpEAAAAAAAAQAAAAEAAAACAAAAAAAAAAAAAXgAAAAOAP####8AAAAAAQAAAAAAahAAAAAAAAEAAAABAAAAAgAAAAAAAAAAABZmJyh4KT1cRm9yU2ltcHtzb2xmJzF9AAAADgD#####AAAAAAEAAAAAAGsQAAAAAAABAAAAAQAAAAIAAAAAAAAAAAAQZih4KT1cRm9yU2ltcHtmfQAAAA4A#####wAAAAAAQAAAAAAAAADACAAAAAAAAAAPZm9ybXVsYWlyZUludDMxAAAAZhAAAAAAAAEAAAACAAAAAgAAAAAAAAAAAAxcdGV4dHtlZGl0MX0AAAAOAP####8B#wAAAL#wAAAAAAAAwDwAAAAAAAAACXNvbEludDMxMQAAAGYQAAAAAAABAAAAAgAAAAIAAAAAAAAAAAAMXEZvclNpbXB7eDB9AAAADgD#####AAAAAAEAD2Zvcm11bGFpcmVJbnQzMgAAAGwaAAAAAAABAAAAAQAAAAIAAAAAAAAAAAAMXHRleHR7bGlzdDF9AAAADgD#####Af8AAADAOwAAAAAAAAAAAAAAAAAAAApsaXN0SW50MzIxAAAAbAwAAAAAAAIAAAABAAAAAgAAAAAAAAAAAD5cYmVnaW57YXJyYXl9e2x9Clx0ZXh0eyt9IApcXCBcdGV4dHstfQpcXCBcdGV4dHswfQpcZW5ke2FycmF5fQAAAA4A#####wAAAAABAA9mb3JtdWxhaXJlSW50MzMAAABuGgAAAAAAAQAAAAEAAAACAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAAA4A#####wH#AAAAwDkAAAAAAAAAAAAAAAAAAAAKbGlzdEludDMzMQAAAG4MAAAAAAACAAAAAQAAAAIAAAAAAAAAAAA#XGJlZ2lue2FycmF5fXtsfQpcdGV4dHt8fSAKXFwgXHRleHR7fHx9ClxcIFx0ZXh0ezB9ClxlbmR7YXJyYXl9AAAADgD#####AAAAAAEAD2Zvcm11bGFpcmVJbnQzNAAAAG0aAAAAAAABAAAAAQAAAAIAAAAAAAAAAAAMXHRleHR7bGlzdDF9AAAADgD#####Af8AAADAOAAAAAAAAD#wAAAAAAAAAApsaXN0SW50MzQxAAAAbQwAAAAAAAIAAAABAAAAAgAAAAAAAAAAAD5cYmVnaW57YXJyYXl9e2x9Clx0ZXh0eyt9IApcXCBcdGV4dHstfQpcXCBcdGV4dHswfQpcZW5ke2FycmF5fQAAAA4A#####wAAAAABAA9mb3JtdWxhaXJlSW50MzUAAABvEAAB####AAAAAQAAAAEAAAACAAAAAAAAAAAADFx0ZXh0e2VkaXQxfQAAAA4A#####wH#AAAAAAAAAAAAAADAIgAAAAAAAAAJc29sSW50MzUxAAAAbxAAAf###wAAAAEAAAACAAAAAgAAAAAAAAAAAAEyAAAADQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABdAAAAZwAAAAsA#####wEAAAAAEAAAAQAAAQEAAABdAAAAZwAAAAcA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAEAAT#pQRYY#4j3AAAAgAAAAAYA#####wEAAAAAEAAAAQAAAQEAAAB#AT#wAAAAAAAAAAAADwD#####AAAAggAAAAkA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAgQAAAIMAAAADAP####8ABW1pbmkxAAItMQAAABAAAAACP#AAAAAAAAAAAAADAP####8ABW1heGkxAAExAAAAAj#wAAAAAAAAAAAAAwD#####AARwYXMxAAExAAAAAj#wAAAAAAAAAAAAEQD#####AQAAAAALAAJPMQDAOAAAAAAAAD#wAAAAAAAAAAABAAAAAIQAAAAMAP####8AAACIAAAABAMAAAAFAAAAhwAAAAQBAAAABQAAAIYAAAAFAAAAhQAAABIA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAgQAAAAsA#####wEAAAAAEAAAAQAAAQEAAACIAAAAigAAABMA#####wEAAAAAEAAAAQAAAAEAAACIAAAAiwAAAAcA#####wEAAAAACwACSjEAwDYAAAAAAADALgAAAAAAAAAAAQABv74ZFMew#VkAAACMAAAACQD#####AQAAAAALAAJJMQAAAAAAAAAAAEAAAAAAAAAAAAABAAAAAIoAAACJAAAAFAD#####AAAAAAAAAQEAAACIAAAAjgAAAI0AAAAAAAAFAAAAhQAAAAIAAAAAAAAAAAAAAAUAAACHAAAAAj#wAAAAAAAAAAAAFQD#####AP8AAAEQAAJUMQAAAAAAAAAAAEAIAAAAAAAAAAAIAAEAAACPP#AAAAAAAAAAAAAAAAAAAAAAAAAABQAAAIUAAAAFAAAAhgAAAAIAAAAAAAAAAAAAAAIAAAAAAAAAAAAAABYA#####wAGbWVzYWJzAAAAjwAAAJAAAAADAP####8AB2ZsZWNoZTEAJWludChtZXNhYnMqMTAwMDAwMDAwMCswLjUpLzEwMDAwMDAwMDAAAAAEAwAAABcCAAAABAAAAAAEAgAAAAUAAACRAAAAAkHNzWUAAAAAAAAAAj#gAAAAAAAAAAAAAkHNzWUAAAAAAAAAGAD#####AAAAfwAAAAkA#####wAAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAkAAAAJMAAAAZAP####8AAAAAABAAAAEAAAACAAAAlAAAAJAAAAAADAD#####AAAAjgAAAAQDAAAABQAAAEAAAAAECgAAAAUAAAACAAAABAkAAAAFAAAAkgAAAAUAAABAAAAACQD#####AP8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAACKAAAAlgAAAAkA#####wD#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAlwAAAJMAAAAZAP####8A#wAAABAAAAEAAAACAAAAmAAAAJcAAAAADQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABoAAAAWwAAAAsA#####wEAAAAAEAAAAQAAAQEAAABoAAAAWwAAAAcA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAEAAT#pQRYY#4j3AAAAmwAAAAYA#####wEAAAAAEAAAAQAAAQEAAACaAT#wAAAAAAAAAAAADwD#####AAAAnQAAAAkA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAnAAAAJ4AAAADAP####8ABm1pbmkxMQACLTEAAAAQAAAAAj#wAAAAAAAAAAAAAwD#####AAZtYXhpMTEAATEAAAACP#AAAAAAAAAAAAADAP####8ABXBhczExAAExAAAAAj#wAAAAAAAAAAAAEQD#####AQAAAAALAAFPAMA4AAAAAAAAP#AAAAAAAAAAAAEAAAAAnwAAAAwA#####wAAAKMAAAAEAwAAAAUAAACiAAAABAEAAAAFAAAAoQAAAAUAAACgAAAAEgD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAACcAAAACwD#####AQAAAAAQAAABAAABAQAAAKMAAAClAAAAEwD#####AQAAAAAQAAABAAAAAQAAAKMAAACmAAAABwD#####AQAAAAALAAFKAMA2AAAAAAAAwC4AAAAAAAAAAAEAAb++GRTHsP1ZAAAApwAAAAkA#####wEAAAAACwABSQAAAAAAAAAAAEAAAAAAAAAAAAABAAAAAKUAAACkAAAAFAD#####AAAAAAAAAQEAAACjAAAAqQAAAKgAAAAAAAAFAAAAoAAAAAIAAAAAAAAAAAAAAAUAAACiAAAAAj#wAAAAAAAAAAAAFQD#####AP8AAAEQAAFUAAAAAAAAAAAAQAgAAAAAAAAAAAgAAQAAAKo#8AAAAAAAAAAAAAAAAAAAAAAAAAAFAAAAoAAAAAUAAAChAAAAAgAAAAAAAAAAAAAAAgAAAAAAAAAAAAAAFgD#####AAdtZXNhYnMxAAAAqgAAAKsAAAADAP####8AB2ZsZWNoZTIAJmludChtZXNhYnMxKjEwMDAwMDAwMDArMC41KS8xMDAwMDAwMDAwAAAABAMAAAAXAgAAAAQAAAAABAIAAAAFAAAArAAAAAJBzc1lAAAAAAAAAAI#4AAAAAAAAAAAAAJBzc1lAAAAAAAAABgA#####wAAAJoAAAAJAP####8AAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAKsAAACuAAAAGQD#####AAAAAAAQAAABAAAAAgAAAK8AAACrAAAAAAwA#####wAAAKkAAAAEAwAAAAUAAABBAAAABAoAAAAFAAAAAgAAAAQJAAAABQAAAK0AAAAFAAAAQQAAAAkA#####wD#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAApQAAALEAAAAJAP####8A#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAALIAAACuAAAAGQD#####AP8AAAAQAAABAAAAAgAAALMAAACyAAAAAAMA#####wAJcmVwSW50MzExAAd0YWJsZWF1AAAABQAAAD4AAAAkAP####8ABnRlcTMxMQAAABkAAAC1AQAAAAACP#AAAAAAAAABAAAAAwD#####AAxyZXNvbHVJbnQzMTEABnRlcTMxMQAAAAUAAAC2AAAAAwD#####AA1yZXNMaXN0SW50MzIxAAxzaShhcG9zLDEsMikAAAAhAAAAAAUAAAAXAAAAAj#wAAAAAAAAAAAAAkAAAAAAAAAAAAAAAwD#####AA1yZXNMaXN0SW50MzMxAAEzAAAAAkAIAAAAAAAAAAAAAwD#####AA1yZXNMaXN0SW50MzQxAAxzaShhcG9zLDIsMSkAAAAhAAAAAAUAAAAXAAAAAkAAAAAAAAAAAAAAAj#wAAAAAAAAAAAAAwD#####AAdyZXNvbHUzAC9mbGVjaGUxPXJlc3VsdGF0RmxlY2hlMSZmbGVjaGUyPXJlc3VsdGF0RmxlY2hlMgAAAAQKAAAABAgAAAAFAAAAkgAAAAUAAABAAAAABAgAAAAFAAAArQAAAAUAAABBAAAAJQD#####AAlyZXBJbnQzNTEAATAAAAACAAAAAAAAAAAAAWUAAAAlAP####8ABnNvbDM1MQANYScqZV4oLWFtYi9hKQAAAAQCAAAABQAAABMAAAAfAAAAIwAAAAAAAAAQAAAABAMAAAAFAAAAGAAAAAUAAAARAAFlAAAAJQD#####AAdzb2wnMzUxAAxhJy9lXihhbWIvYSkAAAAEAwAAAAUAAAATAAAAHwAAACMAAAAAAAAABAMAAAAFAAAAGAAAAAUAAAARAAFlAAAAJAD#####AAZ0ZXEzNTEAAAC9AAAAvAEAAAAAAj#wAAAAAAAAAQAAACQA#####wAHdGVxJzM1MQAAAL4AAAC8AQAAAAACP#AAAAAAAAABAAAAAwD#####AAxyZXNvbHVJbnQzNTEADnRlcTM1MXx0ZXEnMzUxAAAABAsAAAAFAAAAvwAAAAUAAADAAAAADgD#####AAAAAAEAB2Vub25jZTP#####EEA#AAAAAAAAQHF9cKPXCj4AAAAAAAAAAAAAAAAABAMAAAACAAAAAAAAAAAAAAAECAAAAAUAAAABAAAAAkAIAAAAAAAAAbMKXGJlZ2lue2FycmF5fXtsfQpcdGV4dHtQb3VyIHRvdXQgcsOpZWwgJHgkLCAkZV54PjAkIGRvbmMgJGVeey14fT4wJH0gClxcIFx0ZXh0e2RvbmMgJGYnKHgpPVxGb3JTaW1we3NvbGYnMX0kIGEgdG91am91cnMgbGUgc2lnbmUgZGUgJFxGb3JTaW1we3NvbDIxfSQufQpcXCBcdGV4dHskXHRleHRjb2xvcnttYXJvb259e1x0ZXh0e09uIGRlbWFuZGUgbWFpbnRlbmFudCBkZSByZW1wbGlyIGxlIHRhYmxlYXUgZGVzIHZhcmlhdGlvbnMgY2ktZGVzc291cyA6fX0kfQpcXCBcdGV4dHtMZXMgdmFsZXVycyBkb2l2ZW50IMOqdHJlIGRvbm7DqWVzIHNvdXMgbGEgZm9ybWUgbGUgcGx1cyBzaW1wbGUgcG9zc2libGUsIHNhbnMgdXRpbGlzZXIgZGUgcmFjaW5lIGNhcnLDqWUsIGVuIHV0aWxpc2FudCBhdSBtYXhpbXVtIHVuZSBleHBvbmVudGllbGxlLn0KXGVuZHthcnJheX0AAAAlAP####8ABWZvcm0xABooYScqYW1iL2EnK2InKSplXigtYW1iL2EnKQAAAAQCAAAABAAAAAAEAwAAAAQCAAAABQAAABMAAAAFAAAAGAAAAAUAAAATAAAABQAAABUAAAAfAAAAIwAAAAAAAAAQAAAABAMAAAAFAAAAGAAAAAUAAAATAAFlAAAADgD#####AAAA#wEACHNvbHV0aW9u#####xBAgRAAAAAAAEBXNcKPXCj2AAAAAAAAAAAAAAAAAAIAAAAAAAAAAAL8XGJlZ2lue2FycmF5fXtsfQpcdGV4dHskZiQgZXN0IGTDqWZpbmllIHN1ciAkXFIkIHBhciAkZih4KT1cRm9yU2ltcHtmfSQufQpcXCBcdGV4dHtPbiBwZXV0IHBvc2VyICRmPXV2JCBhdmVjICR1KHgpPVxGb3JTaW1we3V9JCBldCAkdih4KT1cRm9yU2ltcHt2fSQufQpcXCBcdGV4dHskdSQgZXQgJHYkIHNvbnQgZMOpcml2YWJsZXMgc3VyICRcUiQgYXZlYyAkdScoeCk9XEZvclNpbXB7dSd9JCBldCAkdicoeCk9XEZvclNpbXB7did9JC59ClxcIFx0ZXh0eyRmJCBlc3QgZG9uYyBkw6lyaXZhYmxlIHN1ciAkXFIkIGNvbW1lIHByb2R1aXQgZGUgZGV1eCBmb25jdGlvbnMgZMOpcml2YWJsZXMgZXQgJGYnPSh1diknPXUndit1dickLn0KXFwgXHRleHR7T24gYSBkb25jICAkZicoeCk9XEZvclNpbXB7Zm9yMTF9PVxGb3JTaW1we2ZvcjEyfSR9ClxcIFx0ZXh0e0RvbmMgJGYnKHgpPVxGb3JTaW1we3NvbGYnMX0kIG91IGVuY29yZSAkZicoeCk9XEZvclNpbXB7c29sZicyfSQgY2FyICRlXnsteH09XGRmcmFjezF9e2VeeH0kLn0KXFwgXHRleHR7Q29tbWUsIHBvdXIgdG91dCByw6llbCAkeCQsICRlXnsteH0+MCQgb24gZW4gZMOpZHVpdCBxdWUgJGYnKHgpJCBhIHRvdWpvdXJzIGxlIHNpZ25lIGRlICRcRm9yU2ltcHtzb2wyMX0kLn0KXFwgXHRleHR7JGZcbGVmdCggXEZvclNpbXB7eDB9IFxyaWdodCk9IFxGb3JTaW1we2Zvcm0xfT1cRm9yU2ltcHtzb2wzNTF9XElme3h6ZXJvcG9zfXs9XEZvclNpbXB7c29sJzM1MX19e30kLn0KXGVuZHthcnJheX0AAAABAP####8AAAD#AQAA#####xBAgRgAAAAAAEBPa4UeuFHsAgAAAAAAAAAAAAAAAAIAAAAAAAAAAAAIc29sdXRpb24AAAAAAAI#8AAAAAAAAAAAAAL###############8=
Sinon :
Utilisez l'icône ![]() pour créer une nouvelle figure sans repère et sans longueur unité.
pour créer une nouvelle figure sans repère et sans longueur unité.
Pour adapter la couleur de fond de la figure à Labomep utilisez l'icône ![]() et choisissez l'item Couleur de fond de la figure puis choisissez comme couleur #f6fafe.
et choisissez l'item Couleur de fond de la figure puis choisissez comme couleur #f6fafe.
En déroulant la barre d'outils des calculs, utilisez l'icône ![]() pour créer deux variables
pour créer deux variables
| Nom de la variable | Valeur mini | Valeur maxi | Pas | Valeur actuelle |
|---|---|---|---|---|
| correction | 0 | 1 | 1 | 0 |
| etape | 1 | 3 | 1 | 1 |
La variable correction servira à afficher des flèches de correction dans notre futur tableau de variations. La variable étape nous servira à n'afficher qu'une partie des consignes suivant l'étape en cours.
La fonction à étudier sera définie par f(x)=(ax+b)e^(-x). Nous nous limiterons à certaines valeurs du couple (a; b), a et b étant des entiers, b positif mais a positif ou négatif.
Déroulez la barre des calculs et, à sa droite, cliquez sur l'icône ![]() qui propose des outils additionnels.
qui propose des outils additionnels.
Choisissez l'item Matrice et créez une matrice à 10 lignes et deux colonnes sont les éléments soient les suivants :
| 1 | 2 |
| 1 | 3 |
| 2 | 1 |
| 2 | 3 |
| 2 | 5 |
| 3 | 1 |
| 3 | 2 |
| 3 | 4 |
| 4 | 1 |
| 4 | 3 |
Utilisez l'icône ![]() pour créer les calculs réels suivants :
pour créer les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| nbEtapes | 3 | Sert à indiquer que l'exercice se fera en deux étapes |
| nbvar | 2 | Nombre de variables servant à choisir les valeurs aléatoires |
| nbcas1 | nbrow(matab) | Nombre de lignes de la matrice matab. On piochera un couple au hasard dans cette matrice |
| nbcas2 | 2 | Nombre de valeurs possibles pour le signe de a |
| r1 | int(rand(0)*nbcas1) | Sert à simuler les valeurs qui seront affectés à r1 lors des répétitions |
| r2 | int(rand(0)*nbcas2) | Sert à simuler les valeurs qui seront affectés à r2 lors des répétitions |
| figureMasqueeEtape1 | 1 | 1 pour vrai : la figure ne sera pas visible à l'étape 1 |
| figureMasqueeEtape2 | 1 | 1 pour vrai : la figure ne sera pas visible à l'étape 2 |
| x1 | 1+rand(0)/10 | Nombre aléatoire. Servira à faire des tests sur une réponse de l'élève |
| x2 | 1.1+rand(0)/10 | Nombre aléatoire. Servira à faire des tests sur une réponse de l'élève |
| x3 | 1.2+rand(0)/10 | Nombre aléatoire. Servira à faire des tests sur une réponse de l'élève |
| absa | matab(r1+1,1) | r1 + 1 représente la ligne de la matrice. Le premier terme de cette ligne sera la valeur absolue de a |
| b | matab(r1+1,2) | r1 + 1 représente la ligne de la matrice. Le premier terme de cette ligne sera la valeur de a |
| a | (-1)^r2*absa | a vaudra absa ou -absa suivant que r1 vaut 1 ou 2 |
Nous donnerons la possibilité à l'utilisateur de donner les valeurs de a et b en paramètres. Dans ce cas les formules donnant a et b que nous avons écrites ci-dessus seront remplacées par ce que l'utilisateur aura choisi comme paramètres. Mais nous voulons nous assurer que dans ce cas les valeurs utilisées par la suite seront bien des entiers premiers entre eux avec b positif.
Nous appellerons a' et b' les valeurs finales que nous utiliserons par la suite et notre fonction sera en fait définie par f(x)=(a'x+b')e^(-x).
Créez les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| gab | pgcd(abs(a),abs(b)) | Le pgcd des valeurs absolues de a et de b |
| a' | a/gab | Valeur réduite de a |
| b1 | abs(b)/gab | Valeur rédudite de b que nous impososns positive |
| b' | si(a'>0&a'=b1,a'+1,b1) | Nous voulons éviter le cas où a' = b' + 1 pour que la dérivée ne s'annule pas en zéro. |
Nous sommes maintenant sûrs que même si l'utilisateur a voulu paramétrer les valeurs de a et b, les valeurs que nous aurons par la suite respectent les conditions que nous voulons respecter.
Créez maintenant les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| e | exp(1) | Valeur approchée de la base de l'exponentielle |
| apos | a'>0 | Ce test renvoie comme valeur 1 si a' est positif et 0 sinon. |
| amb | a'-b' | |
| x0 | amb/a' | Valeur qui annule la dérivée f'(x) |
| xzeropos | x0>0 | Servira dans l'affichage LaTeX donnant l'affichage final de la solution. |
Déroulez la barre d'outils des calculs et utilisez l'icône ![]() pour créer la fonction f de la variable x défiie par la formule : abs(x)<0.000000001
pour créer la fonction f de la variable x défiie par la formule : abs(x)<0.000000001
Cette fonction nous servira à tester si la réponse de l'élève est exacte.
Nous allons maintenant créer des fonctions de deux variables, le noms des variables étant e et x.
Pour cela déroulez la barre d'outils des calculs et, à sa droite, cliquez sur l'icône ![]() . Choisissez l'item Fonction de deux variables.
. Choisissez l'item Fonction de deux variables.
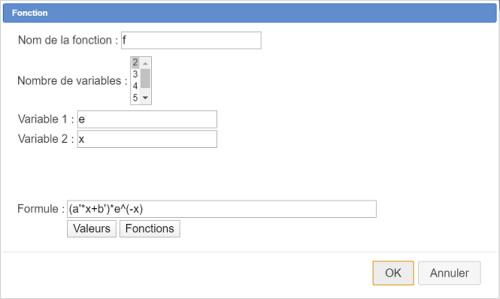
Ci-dessous la première boîte de dialogue telle que vous devez la remplir.
A noter que pour réactiver l'outil vous pouvez utiliser la touche de fonctions F2 (les touches de fonctions ne fonctionnent pas avec la version en ligne de MathGraph32). Attention aussi aux noms des variables : e pour la première variable et x pour la seconde.
| Nom de la fonction de deux variables | Formule | Commentaire |
|---|---|---|
| f | (a'*x+b')*e^(-x) | Formule de la fonction que nous ferons étudier. |
| solf'1 | (-a'*x+amb)*e^(-x) | Première formule acceptée comme réponse finale pour le calcul de la dérivée |
| solf'2 | (-a'*x+amb)/e^x | Deuxième formule acceptée comme réponse finale pour le calcul de la dérivée |
| solf'3 | -(a'*x-amb)*e^(-x) | Troisième formule acceptée comme réponse finale pour le calcul de la dérivée |
| solf'4 | -(a'*x-amb)/e^x | Quatrième formule acceptée comme réponse finale pour le calcul de la dérivée |
Quelques explications :
Lorsque nous testerons la réponse de l'élève pour la calcul de dérivées, si par, exemple le la dérivée vaut (-2x+3)e^(-x) nous accepterons comme réponse finale une des quatre réponses suivantes : (-2x+3)e^(-x), (-2x+3)/e^(x), -(2x-3)e^(-x), -(2x-3)/e^(x) (ou une réponse équivalente). Le fait que nous ayons choisis a' et b' premiers entre eux nous évitera ici d'avoir a tester d'autres réponses possibles où une constante serait factorisée.
Pour contrôler plus facilement les énoncés et formulaires que nous allons créer à chaque étape nous allons utiliser la variable etape que nous avons créée précédemment et 3 macros constructions qui feront changer sa valeur.
Au lieu de les créer manuellement, je vous propose d'automatiser le processus à l'aie d'une macro construction.
Cliquez sur le lien ci-dessous pour télécharger le fichier zip contenant cette construction. Décompressez ensuite ce fichier dans le dossier de votre choix.
Pour utiliser cette construction dans MathGraph32, cliquez d'abord sur l'icône ![]() qui fait apparaître des icônes supplémentaires.
qui fait apparaître des icônes supplémentaires.
Cliquez ensuite sur l'icône ![]() (gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
(gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
Allez dans le dossier où vous avez décompressé le fichier zip contenant la construction et cliquez sur le fichier nommé PreparationMultiEtapes3.mgc.
Cette construction fait maintenant partie de votre figure et peut être utilisée.
Utilisez à nouveau l'icône ![]() et choisissez l'item Implémenter une construction de la figure.
et choisissez l'item Implémenter une construction de la figure.
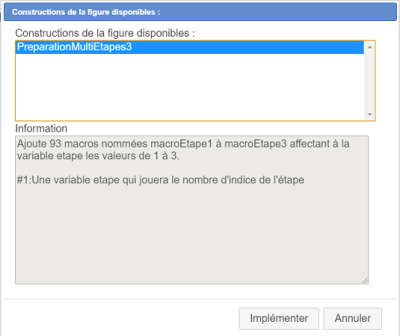
Une boîte de dialogue s'ouvre comme ci-dessous vous présentant les constructions de la figure comme ci-dessous. Notre unique construction est déjà sélectionnée.
Cliquez sur le bouton Implémenter.
Quand on implémente une construction il faut toujours choisir les objets sources numériques en premier.
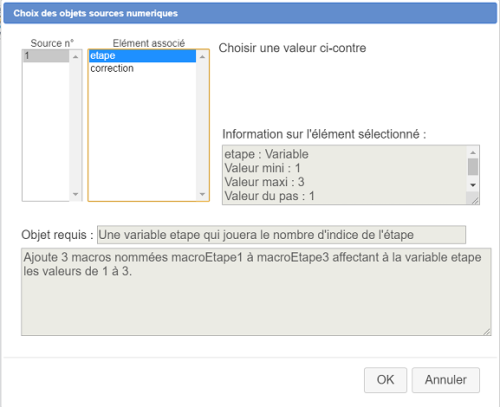
Une boîte de dialogue s'ouvre donc pour choisir le seul objet source.
Comme ci-dessous, affectez à l'élément source n°1 la variable que nous avons nommée etape.
Puis validez par OK.
Maintenant 3 macros sont apparues sur la figure. Par exemple la macro nommée macroEtape3 affectera à la variable nommée etape la valeur 3.
A chaque étape (sauf la première) la macro d'intitulé macroEtape suivi du numéro de l'étape est exécutée par LaboMep avant de passer à cette étape.
Nous allons maintenant préparer l'affichage LaTeX qui contiendra la consigne à afficher à l'étape 1, c'est-à-dire au début de l'exercice.
Déroulez la barre d'outils des affichages et activez l'icône ![]() (affichage LaTeX libre). Cliquez à gauche et au centre de la figure et remplissez la boîte de dialogue comme ci-dessous :
(affichage LaTeX libre). Cliquez à gauche et au centre de la figure et remplissez la boîte de dialogue comme ci-dessous :
Dans le champ code LaTeX entrez le code ci-dessous :
\begin{array}{l}
\text{$f$ est la fonction définie sur $\R$ par $f(x)=\ForSimp{f}$ et $f'$ désigne sa fonction dérivée.}
\\ \text{$\textcolor{maroon}{\text{Dans un premier temps, on demande de calculer }f'(x)}$.}
\\ \text{Le résultat doit être donné sous une forme simple permettant d'étudier le signe de $f'(x)$.}
\end{array}
Dans le champ Angle entrez la formule 0/(etape=1) puis validez.
Pourquoi cette formule dans le champ Angle ?
Dans un exercice multi-étapes, un grand nombre d'affichages LaTeX peuvent être utilisés pour fournir entre autres les consignes, les formulaires et la figure peut sembler surchargée s'ils sont tous affichés en même temps.
Ici, Angle vaudra 0 quand etape est égal à 1 et n'existera pas sinon (car le test etape = 1 renvoie 1 comme valeur s'il est vérifié et 0 sinon).
Donc quand, par exemple, nous cliquerons sur la macro macroEtape2, cet affichage LaTeX n'existera plus et ne sera donc pas affiché.
Chaque \text{} de cet affichage LaTeX fournit une ligne qui sera affichée lors de l'énoncé initial de notre exercice (étape 1).
Créons maintenant un autre affichage LaTeX qui fournira le formulaire à entrer pour le calcul de la dérivée.
Utilisez de nouveau l'outil ![]() (affichage LaTeX libre) et cliquez au-dessous de l'affichage LaTeX précédent.
(affichage LaTeX libre) et cliquez au-dessous de l'affichage LaTeX précédent.
Dans la boîte de dialogue qui s'ouvre, entrez LaTeX suivant :
\text{$f'(x)$ = edit1}
Là aussi, avant de valider, entrez dans le champ Angle la formule 0/(etape = 1)
Pour que ces deux affichages LaTeX soient reconnus par LaboMep pour ce qu'ils contiennent, nous devons leur affecter un tag.
Pour cela, activez l'outil ![]() (protocole dans la barre supérieure d'outils)
(protocole dans la barre supérieure d'outils)
En bas de la liste des objets, sélectionnez l'avant dernier objet (lat1) puis cliquez sur le bouton Changer le tag.
Dans la boîte de dialogue qui s'ouvre, entrez comme tag enonce1 puis validez.
Cliquez sur le dernier objet de la liste (lat2) et, de même, affectez lui le tag formulaire1.
Vous pouvez refermer la boîte de dialogue de protocole.
Nous devons maintenant préparer les objets numériques servant à interpréter la réponse de l'élève dans le formulaire de l'étape 1. Ce formulaire ne contient qu'un seul éditeur de formule (repéré par edit1 dans son code LaTeX).
En déroulant la barre d'outils des calculs, utilisez l'icône ![]() pour créer deux variables.
pour créer deux variables.
Créez la fonction de deux variables nommée rep11 avec comme variables e et x (dans cet ordre) et comme formule 0. (rep11 car il s'agit de l'éditeur n°1 du formulaire de l'étape 1).
Lorsque l'élève proposera une formule pour la dérivée, la formule correspondante sera mise dans ce calcul pour que la figure puisse indiquer si la réponse est bonne ou non.
Pour vérifier si l'élève a entré une des 4 formules que nous considérons comme réponse finale, nous allons créer quatre tests d'équivalence entre solf'1, solf'2, solf'3, solf'4 et rep11 (nommés teqsolf'1, teqsolf'2, teqsolf'3 et teqsolf'4).
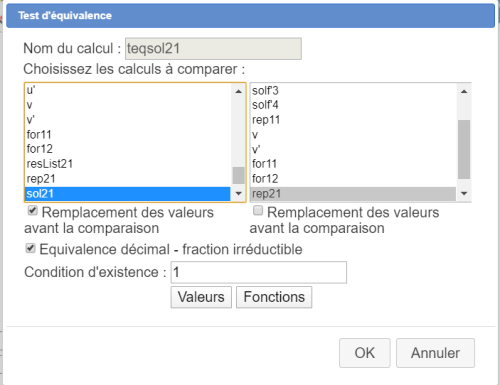
Pour cela, déroulez la barre d'outils des calculs et, à sa droite, cliquez sur l'icône ![]() . Choisissez l'item Test d'équivalence.
. Choisissez l'item Test d'équivalence.
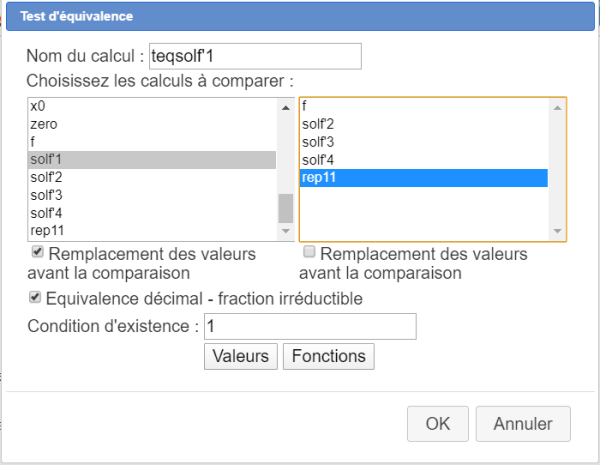
Voici par exemple comment remplir la boîte de dialogue pour la création du premier test d'équivalence :
Attention : il faut cocher la case Remplacement des valeurs à gauche (pour solf'1) mais pas à droite (pour rep11).
Voici comment, par exemple, fonctionne le premier test d'équivalence teqsolf'1 (rappelons que la formule mise dans solf'1 est (-a'*x+amb)*e^(-x)) : les valeurs de a' et b' sont remplacées dans la formule, puis les éventuelles somme avec 0, produits par 1 et quotients par 1 sont réduits, puis on compare la formule avec celle contenue dans rep1. Si (en tenant compte de la commutativité de l'é=addition et la multiplication) ces deux formules sont identiques, le test d'équivalence renvoie comme valeur 1 et sinon il renvoie 0.
Nous devons maintenant créer un calcul nommé resolu11 qui doit valoir 1 si un des quatre tests d'équivalence est vrai (renvoie la valeur 1). Le premier chiffre 1 du nom du calcul est le numéro de l'étape et le second le numéro de l'éditeur de formule dans le formulaire.
Utilisez donc l'icône ![]() pour créer un calcul nommé resolu11 avec la formule ci-dessous (nous utilisons ici l'opérateur logique | de MathGraph32) :
pour créer un calcul nommé resolu11 avec la formule ci-dessous (nous utilisons ici l'opérateur logique | de MathGraph32) :
teqsolf'1|teqsolf'2|teqsolf'3|teqsolf'4
Dans la cas où l'élève n'a pas donné une des 4 réponses finales attendues, il nous faut aussi savoir s'il a donné une formule exacte pour le calcul de la dérivée. Pour cela il faut créer un calcul nommé exact11.
Auparavant créez à l'aide de l'icône ![]() (barre d'outils des calculs) la fonction nommée zero de la variable x définie par la formule suivante :
(barre d'outils des calculs) la fonction nommée zero de la variable x définie par la formule suivante :
abs(x)<0.000000001
Cette fonction revoie 1 si son argument x a une valeur absolue inférieure à 10^(-9).
Créez ensuite un calcul réel nommé exact11 avec comme formule :
zero(solf'1(e,x1)-rep11(e,x1))&zero(solf'1(e,x2)-rep11(e,x2))&zero(solf'1(e,x3)-rep11(e,x3))
Nous vérifions donc à l'aide de 3 valeurs aléatoires que la différence entre la formule de solf'11 et la formule contenue dans rep11 est nulle à 10^(-9) près (la valeur e passée en paramètre est le calcul nommé e que nous avons défini au début par la formule exp(1)).
Nous allons maintenant passer à la deuxième étape de notre exercice.
Dans la barre d'outils supérieures, actives l'outil ![]() (exécution de macro) puis cliquez sur la macro macroEtape2. La variable etape a maintenant pour valeur 2. Nos affichages LaTeX précédents ne sont plus visibles.
(exécution de macro) puis cliquez sur la macro macroEtape2. La variable etape a maintenant pour valeur 2. Nos affichages LaTeX précédents ne sont plus visibles.
Nous devons créer un affichage LaTeX de tag enonce2 contenant des éléments de correction pour la question précédente et la consigne pour l'étape 2.
Mais auparavant bous allons créer des objets numériques qui seront utilisés dans cet affichage LaTeX.
Utilisez l'icône ![]() pour créer deux fonction numérique de la variable x comme ci-dessous :
pour créer deux fonction numérique de la variable x comme ci-dessous :
| Nom de la fonction | Formule |
|---|---|
| u | a'*x+b' |
| u' | a' |
Déroulez la barre d'outils des calculs et, à sa droite, cliquez sur l'icône ![]() . Choisissez l'item Fonction de deux variables et créez les deux fonctions de deux variables e et x avec les formules ci-dessous :
. Choisissez l'item Fonction de deux variables et créez les deux fonctions de deux variables e et x avec les formules ci-dessous :
| Nom de la fonction | Formule |
|---|---|
| v | e^(-x) |
| v' | -e^(-x) |
| for11 | a'*e^(-x)+(a'*x+b')*(-e^(-x)) |
| for12 | e^(-x)*(a'-(a'*x+b')) |
Déroulez la barre des affichages et cliquez sur l'icône ![]() (affichage LaTeX libre).
(affichage LaTeX libre).
Cliquez à gauche et au centre de la figure. La boîte de dialogue s'ouvre.
Dans le champ Code LaTeX entrez ce qui suit :
\begin{array}{l}
\text{$f$ est définie sur $\R$ par $f(x)=\ForSimp{f}$.}
\\ \text{On peut poser $f=uv$ avec $u(x)=\ForSimp{u}$ et $v(x)=\ForSimp{v}$.}
\\ \text{$u$ et $v$ sont dérivables sur $\R$ avec $u'(x)=\ForSimp{u'}$ et $v'(x)=\ForSimp{v'}$.}
\\ \text{$f$ est donc dérivable sur $\R$ comme produit de deux fonctions dérivables et $f'=(uv)'=u'v+uv'$.}
\\ \text{On a donc $f'(x)=\ForSimp{for11}=\ForSimp{for12}$}
\\ \text{Donc $f'(x)=\ForSimp{solf'1}$ ou encore $f'(x)=\ForSimp{solf'2}$ car $e^{-x}=\dfrac{1}{e^x}$.}
\\ \text{$\textcolor{maroon}{\text{Compléter ci-dessous de la façon la plus simple possible :}}$}
\end{array}
Avant de valider, entrez dans le champ Angle la formule : 1/(etape=2).
Utilisez de nouveau l'outil de création d'affichage LaTeX libre pour créer, sous le précédent, un affichage LaTeX dont le code LaTeX soit :
\text{Pour tout réel $x$, $e^{-x}$ list1 donc $f'(x)$ a le signe de edit1}
Avant de valider, entrez dans la formule Angle : 0/(etape = 2)
Ici le formulaire est une phrase ave un éditeur de formule repéré par edit1 et une liste déroulante repérée par list1.
Les items proposés par cette liste déroulante doivent être contenus dans un autre affichage LaTeX.
Activez la couleur rouge (ce n'est pas indispensable) et, à côté de l'affichage LaTeX précédent, créez donc un autre affichage LaTeX dont le code LaTeX soit :
\begin{array}{l}
\text{>0}
\\ \text{<0}
\end{array}
Avant de valider entrez comme angle : 0/(etape = 2)
Il nous faut maintenant affecter des tags à ces trois derniers affichages LaTeX.
Utilisez l'outil ![]() de la barre supérieure et, en bas de la liste, utilisez le bouton Changer le tag pour affecter les tags suivants :
de la barre supérieure et, en bas de la liste, utilisez le bouton Changer le tag pour affecter les tags suivants :
| Elément | tag | Commentaire |
|---|---|---|
| lat3 | enonce2 | Le 2 car c'est l'énoncé de la deuxième étape |
| lat4 | formulaire2 | Le 2 car c'est le formulaire de la deuxième étape |
| lat5 | list21 | Le 2 car il s'agir de la deuxième étape et le 1 car il fournit les items de la première liste de ce formulaire. |
Créons maintenant les objets numériques nécessaires pour vérifier la réponse de l'élève à l'étape 2.
Créez un calcul réel nommé resList21 avec comme formule 1. Ce calcul renvoie l'indice du bon résultat dans la première (et unique) liste déroulante du formulaire de l'étape2 (la liste repérée par list1 dans le code LaTeX de ce formulaire). Ici la bonne réponse est le premier item de la liste (>0).
Créez trois fonctions réelles de deux variables e et x (dans cet ordre) comme indiqué ci-dessous :
| Nom de la fonction | Formule | Commentaire |
|---|---|---|
| rep21 | 0 | Contiendra la réponse de l'élève au premier éditeur mathquill du formulaire de l'étape 2 (celui repéré par edit1 dans le code LaTeX de ce formulaire) |
| sol21 | -a'*x+amb | Première formule acceptée comme bonne pour la réponse dans rep21 |
| sol'21 | -(a'*x-amb) | deuxième formle acceptée comme bonne pour la réponse dans rep21 |
Créons maintenant deux test d'équivalence entre sol21, sol'21 et rep21.
Pour cela, déroulez la barre d'outils des calculs et, à sa droite, cliquez sur l'icône ![]() . Choisissez l'item Test d'équivalence.
. Choisissez l'item Test d'équivalence.
| Nom du test d'équivalence | Entre ? | Commentaire |
|---|---|---|
| teqsol21 | entre sol21 et rep21 | Cocher remplacement des valeurs pour sol21 mais pas pour rep21 |
| teqsol'21 | entre sol'21 et rep21 | Cocher remplacement des valeurs pour sol'21 mais pas pour rep21 |
Voici par exemple ci-dessous comment créer teqsol21 :
Créez avec l'icône ![]() maintenant les deux calculs réels suivants destinés à informer LaboMep si la réponse est acceptée comme bonne (pour le premier) ou exacte (pour le second) :
maintenant les deux calculs réels suivants destinés à informer LaboMep si la réponse est acceptée comme bonne (pour le premier) ou exacte (pour le second) :
| Nom du calcul | Formule |
|---|---|
| resolu21 | teqsol21|teqsol'21 |
| exact21 | zero(sol21(e,x1)-rep21(e,x1))&zero(sol21(e,x2)-rep21(e,x2))&zero(sol21(e,x3)-rep21(e,x3)) |
Passons à l'étape 3. Dans la barre d'outils supérieure cliquez sur l'icône ![]() (exécution d'une macro) puis cliquez sur la macro macroEtape3. Nos affichages LaTeX disparaissent.
(exécution d'une macro) puis cliquez sur la macro macroEtape3. Nos affichages LaTeX disparaissent.
Cette étape 3 va être spéciale car ce sera une étape à validation interne qui consistera à remplir un tableau des variations.
Pour préparer ce tableau des variations (avec signe de la dérivée) nous allons utiliser une macro construction que vous pouvez télécharger ci-dessous dans un fichier zip :
tableauvaravecderiv1valeuretape3.zip
Décompressez ce fichier zip.
Cliquez ensuite sur l'icône ![]() (gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
(gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
Allez dans le dossier où vous avez décompressé le fichier zip contenant la construction et cliquez sur le fichier nommé TableauVarAvecDeriv1ValeursEtape3.mgc. La construction fait maintenant partie de la figure.
Pour être exécutée, cette macro construction aura besoin de deux objets sources :
- un calcul qui ne sert qu'à créer les objets numériques du tableau.
- une variable qui doit pour avoir 0 si on veut que la correction pour les flèches mal placées soit visible.
- deux calculs donnant le résultat des deux flèches du tableau (de valeur 1 si la flèche doit monter, -1 si elle doit descendre et 0 si elle doit être horizontale).
- un point qui servira à indiquer le bord du tableau en haut et à gauche.
Utilisez l'icône ![]() pour créer les calculs réels suivants :
pour créer les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| tableau | 1 | Ne sert qu'à générer les objets numériques qui serviront à vérifier les réponses de l'élève |
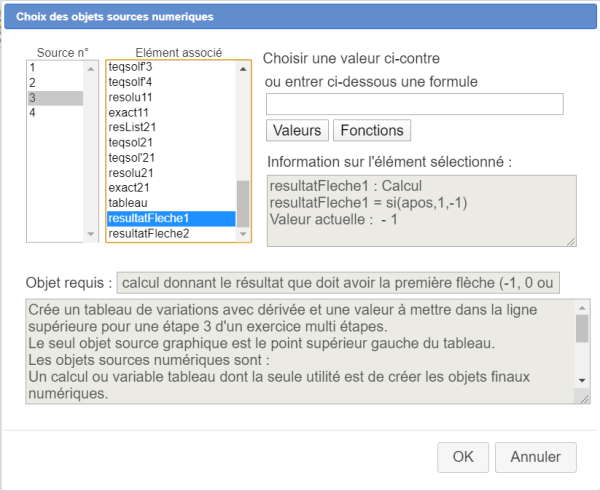
| resultatFleche1 | si(apos,1,-1) | Si a est positif, la bonne réponse dans la première case du tableau est une flèche montante sinon une flèche descendante |
| resultatFleche2 | si(apos,-1,1) | Si a est positif, la bonne réponse dans la deuxième case du tableau est une flèche descendante, sinon une flèche descendante |
Utilisez l'icône ![]() pour créer un point libre en haut et à gauche de la figure.
pour créer un point libre en haut et à gauche de la figure.
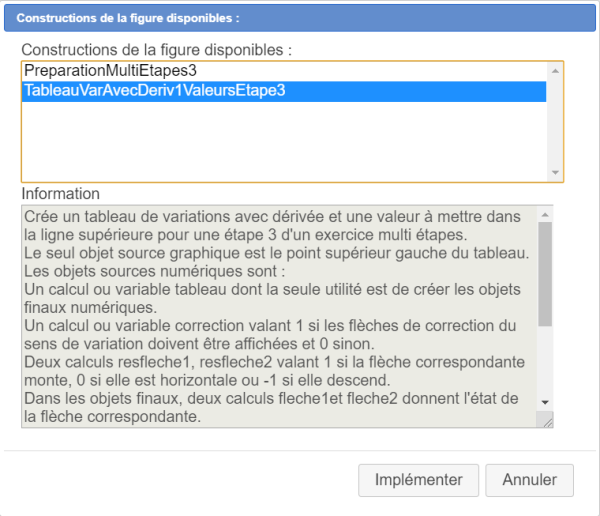
Activez de nouveau l'icône ![]() (gestion des constructions) et choisissez l'item Implémenter une constructionde la figure.
(gestion des constructions) et choisissez l'item Implémenter une constructionde la figure.
Choisissez la deuxième construction de la liste comme ci-dessous puis cliquez sur le bouton Implémenter :
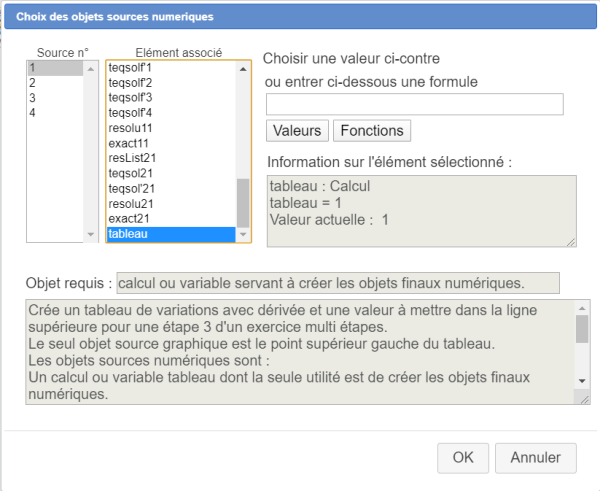
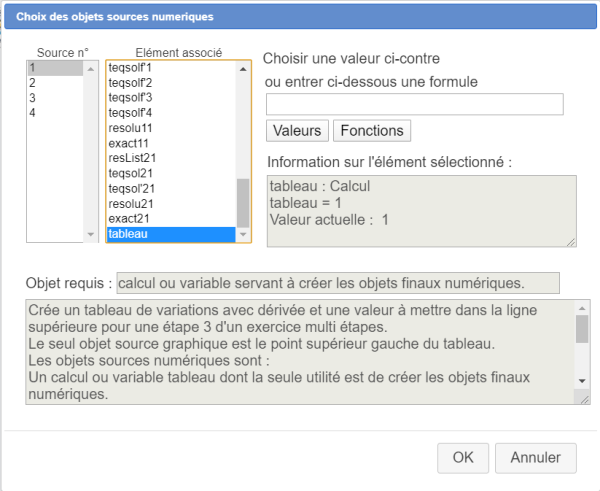
Une boîte de dialogue s'ouvre pour le choix des objets sources de la constriction. Affectez à l'objet source n°1 le calcul tableau comme ci-dessous :
Affectez à l'objet source n°2 la variable correction comme ci-dessous :
Affectez à l'élément source n°3 le calcul resultatFleche1 comme ci-dessous :
Faites de même pour affecter à l'élément source n°4 le calcul resultatFleche2 puis validez la boîte de dialogue.
Il vous est ensuite demandé de cliquer sur le point donnant le coin supérieur gauche du tableau. Cliquez sur le point libre que vous venez de créer.
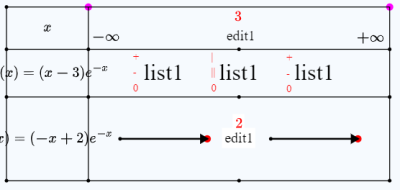
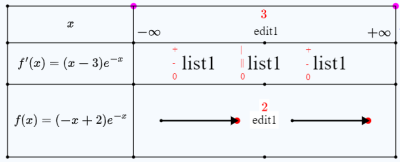
Le tableau apparaît. Avec lui ont aussi été créés des objets numériques.
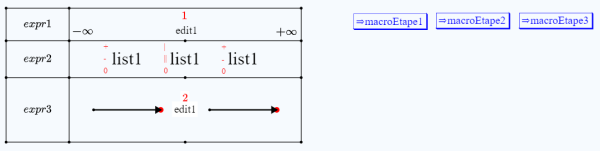
Votre figure ressemble à ceci :
Pour pouvoir modifier les objets créés par cette macro construction, il faut fusionner les macro constructions de la figure. Pour ce faire utilisez l'icône ![]() (gestion des constructions) et activez l'item Fusionner les constructions implémentées de la figure.
(gestion des constructions) et activez l'item Fusionner les constructions implémentées de la figure.
Si vous utilisez l'outil ![]() de modification d'objet numérique vous verrez par exemple que la construction a ajouté un calcul nommé etapeInterne3 dont la formule est 1+0*tableau.
de modification d'objet numérique vous verrez par exemple que la construction a ajouté un calcul nommé etapeInterne3 dont la formule est 1+0*tableau.
Pourquoi cette formule ? Pour que ce calcul dépende du calcul tableau et puisse être un objet finale de la construction. Vous pouvez bien sûr remplacer maintenant cette formule par 1. La présence de ce calcul de valeur 1 informe LaboMep que la troisème étape est à validation interne et donc que la validation de la formule se fait sur la figure elle-même et pas dans un unique formulaire comme aux deux premières étapes. Labomep devra alors rechercher par exemple si la figure contient des affichages LaTeX dont le tag soit formulaireInt3 suivi d'un numéro et les traiter en les remplaçant par des formulaires d'édition placés sur la figure.
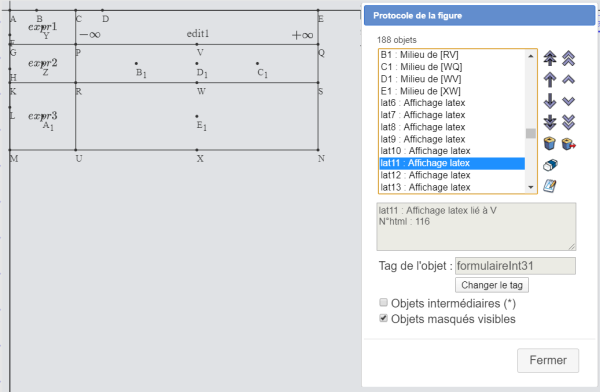
Utilisez l'outil ![]() (protocole) et naviguez dans les objets créez avec la flèche ↓ jusqu'à arriver à l'affichage LaTeX de tag formulaireInt31 (le int pour interne) comme ci-dessous.
(protocole) et naviguez dans les objets créez avec la flèche ↓ jusqu'à arriver à l'affichage LaTeX de tag formulaireInt31 (le int pour interne) comme ci-dessous.
En rencontrant un affichage LaTeX avec un tel tag, LabeMep va savoir qu'il faut remplacer cet affichage LaTeX par un éditeur.
Le code LaTex de cet affichage LaTeX est : \text{edit1}
Il n'y aura donc dans cet éditeur qu'un éditeur de formule mathquill.
A l'étape 3 de l'exercice, cet affichage LaTeX disparaîtra et sera remplacé par un éditeur de formule mathquill. Cet éditeur de formule aura le même alignement par rapport au point que l'affichage LaTeX (ici par exemple centré horizontalement et verticalement aligné au-dessus du point) et la taille des caractères de cet éditeur sera la taille choisie pour les caractères de cet affichage LaTeX (qui est ici de 16 par exemple).
Nous verrons par la suite quels sont les objets numériques créés par la construction qui servent à vérifier si uen bonne réponse a été entrée dans cet éditeur (il faudra bien sûr les adapter).
Toujours en restant dans le protocole de la figure, descendez d'un cran vers l'affichage LaTeX suivant.
Vous voyez qu'il s'agit d'un affichage LaTeX rouge de tag solInt311.
Cet affichage LaTeX est là pour fournir ce qu'il faudra afficher à la place de l'éditeur mathquill du premier formulaire lors de la phase de correction de l'étape 3.
Pourquoi ce tag solInt311 ? Parce que, dans l'éditeur de formule de tag formulaireInt31, il fournit la correction au premier éditeur mathquill de cet formulaire (qui n'en contient qu'un), d'où le chiffre 1 ajouté à la fin du tag.
Nous allons modifier cet affichage LaTeX pour l'adapter à notre exercice en restant dans la boîte de dialogue de protocole.
Cliquez à droite sur la petite icône ![]() .
.
La boîte de dialogue de modification de cet affichage LaTeX apparaît. Le code LaTeX actuel est 1. Remplacez le par le code LaTeX suivant puis validez pour retourner dans le protocole de la figure :
\ForSimp{x0}
Vous pouvez voir vers la fin de la liste deux calculs nommés repInt311 et resoluInt311. Ils ont été créés pour vous par la construction.
Le premier servira à contenir la réponse de l'élève dans cet éditeur mathquill et le second devra contenir 1 si la réponse contenue dans repInt311 est acceptée comme bonne. Le second devra être modifié pour s'adapter à notre exercice (pour le moment ces deux calculs contiennent comme formule tableau).
Descendez dans la liste des objets pour arriver à l'affichage LaTeX de tag formulaireInt32.
Grâce à ce tag, LaboMep va savoir que cet affichage LaTeX devra être remplacé par un autre éditeur lors du passage à l'étape3.
Le contenu de ce nouvel affichage LaTeX est \text{list1}. Il devra donc être remplacé par un éditeur formé d'une seule liste déroulante.
En descendant encore d'un cran dans la liste des objets créés, vous voyez un affichage LaTeX rouge dont le tag est listInt321. (listInt32 car il est associé au formulaire de tag listInt21 et le 1 final car c'est la liste n° 1 dans ce formulaire qui ne contient qu'une liste).
Son code LaTeX est :
\begin{array}{l}
\text{+}
\\ \text{-}
\\ \text{0}
\end{array}
Chaque \text{} fournit un des items que la liste devra proposer. Ici, dans l'ordre, +, - et 0.
Si vous descendez vers la fin de la liste des objets, vous pourrez y voir un calcul nommé resList321.
Ce calcul devra être adapté pour notre exercice en revoyant l'indice de l'item que l'élève doit choisir dans la liste déroulante.
Vous pouvez voir ainsi que la construction a créés 5 affichages LaTeX de tag formulaireInt31, formulaireInt32, formulaireInt33, formulaireInt34 et formulaireInt35.
Le premier sera associé à un éditeur de formule mathquill (celui de la ligne du haut du tableau), les trois suivants à des listes déroulantes (celles de la ligne pour les signes) et le dernier à la valeur de l'extremum sur la dernière ligne du tableau.
On pourrait bien sûr imaginer de créer tout cela “à la main” mais la macro construction (créée par votre serviteur :)) permet d'accéler le processus.
Quittez la boîte de dialogue de protocole.
Pour valider la réponse de l'élève dans l'éditeur mathquill qui sera généré à la première ligne du tableau nous allons créer un test d'équivalence.
Pour cela, déroulez la barre d'outils des calculs et, à sa droite, cliquez sur l'icône ![]() . Choisissez l'item Test d'équivalence.
. Choisissez l'item Test d'équivalence.
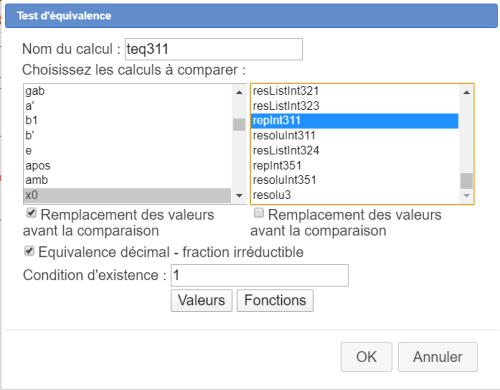
Créez un test d'équivalence nommé teq311 comme ci-dessous (le nom choisi n'est pas imposé par le modèle) :
La construction a créé pour nous un calcul nommé resolu311 avec, comme formule provisoire tableau. Nous devons remplacer cette formule par teq311 mais pour cela il nous faut d'abord reclasser teq311 pour qu'il figure avant resolu311 dans la liste des objets créés.
Pour cela activez l'outil protocole ![]() de la barre supérieure, descendez dans la liste des objets créés et sélectionnez le calcul teq311.
de la barre supérieure, descendez dans la liste des objets créés et sélectionnez le calcul teq311.
A droite de la boîte de dialogue cliquez sur le bouton ![]() (reclassement d'un rang vers le haut) jusqu'à ce que teq311 se retrouve avant le calcul resolu311 comme ci-dessous :
(reclassement d'un rang vers le haut) jusqu'à ce que teq311 se retrouve avant le calcul resolu311 comme ci-dessous :
Maintenant sélectionnez dans la liste le calcul resolu311. Cliquez sur le petit bouton ![]() pour modifier sa formule.
pour modifier sa formule.
Sa formule actuelle est tableau. Remplacez la par teq311 et validez pour revenir au protocole.
En restant dans la boîte de dialogue de protocole, utilisez l'icône ![]() pour modifier la formule des calculs suivants:
pour modifier la formule des calculs suivants:
| Nom du calcul | Ancienne formule | Nouvelle formule | Commentaire |
|---|---|---|---|
| resListInt321 | tableau | si(apos,1,2) | Si a' est positif, il faut un signe + dans la première case de la ligne des signes de la dérivée(premier item de la liste associée) et sinon un signe - |
| resListInt331 | tableau | 3 | Il faut un zéro au dessous de la valeur qui annule la dérivée |
| resListInt341 | tableau | si(apos,2,1) | Si a' est positif, il faut un signe - dans la première case de la ligne des signes de la dérivée(deuxième item de la liste associée) et sinon un signe + |
Nous devons maintenant gérer l'éditeur de la deuxième ligne du tableau (maximum ou minimum de la fonction).
Restez dans la boîte de dialogue de protocole. Vous y voyez la présence de deux calculs repInt351 (qui est là pour contenir la réponse de l'élève dans l'éditeur mathquill associé au LaTeX de tag formulaireInt35) et resolu351.
Nous allons gérer la réponse de l'élève avec des tests d'équivalence et, pour ce faire, il va nous falloir utiliser une fonction de la variable e pour la réponse et pas un calcul. Il va donc falloir détruire ce calcul et le remplacer par une fonction.
Dans la boîte de dialogue de protocole, sélectionnez donc le calcul repInt351 et cliquez à droite sur l'icône ![]() pour le supprimer.
pour le supprimer.
Quittez la boîte de dialogue de protocole, déroulez la barre des calculs et activez l'icône ![]() de création d'une fonction numérique.
de création d'une fonction numérique.
Créez une fonction de la variable e nommée repInt351 avec comme formule 0. N'oubliez pas de décocher la case Tracer courbe comme ci-dessous :
Procédez de même pour créer deux autres fonctions de la variable e comme indiquez ci-dessous (n'oubliez pas de décocher la case Tracer courbe) :
| Nom de la fonction | Formule |
|---|---|
| sol351 | a'*e^(-amb/a) |
| sol'351 | a'/e^(amb/a) |
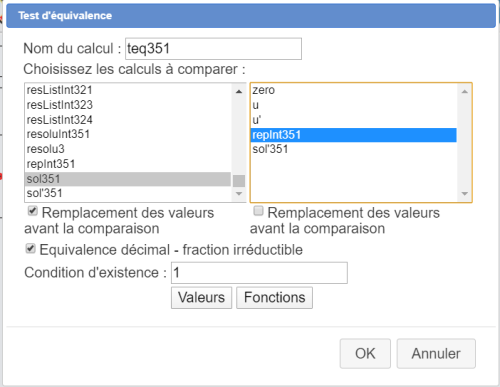
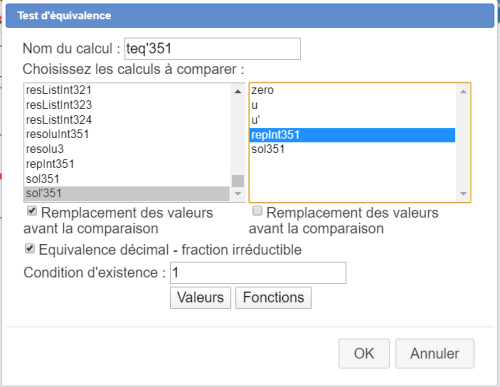
Nous allons maintenant créer deux tests d'équivalence nommes teq351 et teq'351 pour tester la réponse de l'élève avec ces deux formules.
Déroulez la barre d'outils des calculs et, à sa droite, cliquez sur l'icône ![]() . Choisissez l'item Test d'équivalence.
. Choisissez l'item Test d'équivalence.
Créez les tests comme indiqué ci-dessous :
Pour que le calcul resoluInt351 puisse utiliser ces deux tests d'équivalence nous allons le reclasser.
Activez de nouveau l'outil protocole ![]() et sélectionnez resoluInt351.
et sélectionnez resoluInt351.
A droite cliquez sur l'icône ![]() qui reclasse un objet au maximum vers la fin de la liste des objets créés. Notre calcul se retrouve en fin de liste.
qui reclasse un objet au maximum vers la fin de la liste des objets créés. Notre calcul se retrouve en fin de liste.
Ce calcul resoluInt351 étant sélectionné dans la liste, cliquez sur l'icône ![]() pour modifier sa formule.
pour modifier sa formule.
Sa formule actuelle est tableau. Remplacez là par :
teq351|teq'351
Vous remarquerez que la macro construction a aussi créé un calcul nomme resolu3 avec comme formule fleche1=resultatFleche1&fleche2=resultatFleche2.
La présence d'un tel calcul est nécessaire pour une étape de validation interne (ici l'étape 3) dans le cas où une action sur la figure est requise. Ici l'élève devra modifier les deux flèches pour que leur position soit en accord avec les positions attendues (données dans les calculs résultatFleche1 et resultatFleche2). Tour cela a été géré par la macro construction. Voyant qu'un tel calcul est présent, LaboMep vérifiera que sa valeur est bien 1 pour s'assurer que l'action sur la figure à cette étape a été correcte (ici placer les flèches dans la bonne position).
Il nous faut maintenant modifier les affichages LaTeX dans la colonne de gauche du tableau.
Quittez la boîte de dialogue de protocole et, dans la barre supérieure d'outils, activez l'outil ![]() (modification graphique).
(modification graphique).
Cliquez sur le premier affichage LaTeX de la colonne de gauche (expr1). Remplacez son code LaTeX par x et validez.
Cliquez sur le deuxème affichage LaTeX de la colonne de gauche (expr2). Remplacez son code LaTeX par le code suivant et validez et validez.
f'(x)=\ForSimp{solf'1}
Cliquez sur le troisième affichage LaTeX de la colonne de gauche (expr3). Remplacez son code LaTeX par le code suivant et validez et validez.
f(x)=\ForSimp{f}
Vous avez sans doute remarqué qu'il n'y a pas assez de place dans la colonne de gauche.
Avec l'outil de capture ![]() , capturez les deux points en rose ci-dessous pour que les affichages LaTeX de gauche ne débordent pas comme ci-dessous :
, capturez les deux points en rose ci-dessous pour que les affichages LaTeX de gauche ne débordent pas comme ci-dessous :
Vous pouvez maintenant utiliser l'outil gomme ![]() pour masquer les points aux intersections des lignes et colonnes du tableau et les 5 affichages LaTeX rouge (qui contiennent les items pour les listes déroulantes).
pour masquer les points aux intersections des lignes et colonnes du tableau et les 5 affichages LaTeX rouge (qui contiennent les items pour les listes déroulantes).
Ils nous reste à préparer deux affichages LaTeX, l'un donnant des éléments de correction pour l'étape 2 et la consigne pour l'étape 3 et un autre qui donnera la correction finale de l'exercice une fois que l'élève aura tout terminé.
Activez l'icône ![]() (affichage LaTeX libre).
(affichage LaTeX libre).
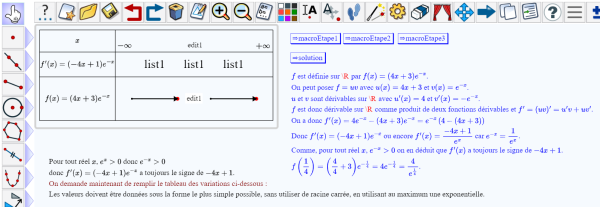
Cliquez au-dessous du tableau et à gauche et entrez comme code LaTeX le code suivant :
\begin{array}{l}
\text{Pour tout réel $x$, $e^x>0$ donc $e^{-x}>0$}
\\ \text{donc $f'(x)=\ForSimp{solf'1}$ a toujours le signe de $\ForSimp{sol21}$.}
\\ \text{$\textcolor{maroon}{\text{On demande maintenant de remplir le tableau des variations ci-dessous :}}$}
\\ \text{Les valeurs doivent être données sous la forme le plus simple possible, sans utiliser de racine carrée, en utilisant au maximum une exponentielle.}
\end{array}
Avant de valider entrez dans le champ Angle la formule suivante puis validez :
0/(etape=3)
Ainsi cet affichage LaTeX ne sera visible qua quand la variable etape a pour valeur 3.
Notre affichage LaTeX de correction a besoin d'afficher la formule d'une autre fonction.
Utilisez l'icône ![]() pour créer une fonction nommée form1 de la variable e avec la formule ci-dessous (pensez à décocher la case Tracer courbe):
pour créer une fonction nommée form1 de la variable e avec la formule ci-dessous (pensez à décocher la case Tracer courbe):
(a'*amb/a'+b')*e^(-amb/a')
Maintenant, avec l'icône ![]() créez un autre affichage LaTeX qui fournira la correction de l'exercice.
créez un autre affichage LaTeX qui fournira la correction de l'exercice.
Cliquez sous l'affichage précédent et entrez comme code LaTeX le code suivant :
\begin{array}{l}
\text{$f$ est définie sur $\R$ par $f(x)=\ForSimp{f}$.}
\\ \text{On peut poser $f=uv$ avec $u(x)=\ForSimp{u}$ et $v(x)=\ForSimp{v}$.}
\\ \text{$u$ et $v$ sont dérivables sur $\R$ avec $u'(x)=\ForSimp{u'}$ et $v'(x)=\ForSimp{v'}$.}
\\ \text{$f$ est donc dérivable sur $\R$ comme produit de deux fonctions dérivables et $f'=(uv)'=u'v+uv'$.}
\\ \text{On a donc $f'(x)=\ForSimp{for11}=\ForSimp{for12}$}
\\ \text{Donc $f'(x)=\ForSimp{solf'1}$ ou encore $f'(x)=\ForSimp{solf'2}$ car $e^{-x}=\dfrac{1}{e^x}$.}
\\ \text{Comme, pour tout réel $x$, $e^{-x}>0$ on en déduit que $f'(x)$ a toujours le signe de $\ForSimp{sol21}$.}
\\ \text{$f\left( \ForSimp{x0} \right)= \ForSimp{form1}=\ForSimp{sol351}\If{xzeropos}{=\ForSimp{sol'351}}{}$.}
\end{array}
Il nous faut donner des tags à ces affichages LaTeX pour qu'ils soient bien reconnus.
Utilisez l'outil protocole ![]() et sélectionnez l'avant dernier affichage LaTex, puis donnez lui le tag enonce3 à l'aide du bouton Changer le tag.
et sélectionnez l'avant dernier affichage LaTex, puis donnez lui le tag enonce3 à l'aide du bouton Changer le tag.
Procédez de même pour donner le tag solution au dernier affichage LaTeX de la figure puis quitez la boîte de dialogue de protocole.
Quand nous avons implémenté notre construction nous avons fourni comme objet source une variable correction. Quand cette variable vaut 1, des flèches rouges apparaissent en plus des flèches noirs sur la figure pour montrer quelle était la bonne position dans le cas où la flèche noire n'est pas dans la position attendue (qui était donnée dans les calculs resultatFleche1 et resultatFleche2).
A la fin de l'exercice, LaboMep cherchera si la figure contient une macro d'intitulé solution et si elle existe il l'exécutera, modifiant ainsi l'état de la figure.
Déroulez la barre d'outils des affichages et, à sa droite, cliquez sur l'icône ![]() (création de macro).
(création de macro).
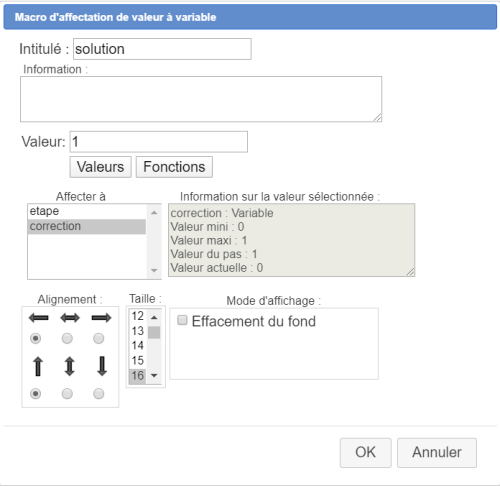
Choisissez l'item Macro d'affectation de valeur à variable et cliquez par exemple au-dessous des trois macros déjà présentes sur la figure.
Créez ainsi une macro d'intitulé solution affectant à la variable correction la valeur 1 comme ci-dessous :
Si vous voulez voir l'effet de cette macro sur la figure, activez dans la barre supérieure l'outil ![]() (exécution de macro) puis cliquez sur la macro solution. Vous devez voir apparaître les flèches rouges de correction.
(exécution de macro) puis cliquez sur la macro solution. Vous devez voir apparaître les flèches rouges de correction.
Si vous avez exécuté la macro solution, utilisez l'icône ![]() (annulation de la dernière action) pour remettre la variable correction dans son état précédent (valeur 0).
(annulation de la dernière action) pour remettre la variable correction dans son état précédent (valeur 0).
Il nous reste une dernière chose à faire : déterminer les dimensions de votre tableau de variations pour que LaboMep n'affiche que la partie utile de la figure (cela servira dans les paramètres de la ressource).
Dans la barre supérieure, activez l'outil ![]() (options de la figure).
(options de la figure).
Cochez la case Utiliser un cadre de dimensions données et validez pour refermer la boîte de dialogue.
Un grand cadre grisé est apparu autour de la figure. Vous pouvez avec l'outil de capture le réduire ou l'agrandir en capturant ses bords ou son coin inférieur droit.
Réduisez -le de façon à encadrer le tableau comme ci-dessous :
Activez de nouveau l'outil ![]() (options de la figure).
(options de la figure).
Vous pouvez maintenant y lire les dimensions de votre cadre comme ci-dessous (avec des valeurs peut-être un peu différentes) :
Notez bien ces dimensions qui nous serviront lors du paramétrage de la ressource.
Une remarque avant de passer à la création de la ressource.
De la façon dont nous avons procédé, le tableau de variation est visible dans la figure même quand la variable etape vaut 1 ou 2, ce qui n'est pas gênant ici car la figure ne sera pas affichée à ces étapes puisque nous avons créé deux calculs nommés figureMasqueeEtape1 et figureMasqueeEtape2 de valeur 1.
Si nous avions voulu que le tableau ne soit visible qu'à l'étape 3, après avoir exécuté la macro macroEtape3, au lieu de prendre un point libre pour jouer le rôle du coin supérieur gauche, nous aurions pu par exemple utiliser l'astuce suivante : créer deux points libres, nommons les A et B, avec B en haut et à gauche de la figure, utiliser l'outil ![]() pour créer l'image de B par l'homothétie de centre A et rapport 1/(etape=3) et utiliser ce point lors de l'implémentation de la construction créant le tabelau.
pour créer l'image de B par l'homothétie de centre A et rapport 1/(etape=3) et utiliser ce point lors de l'implémentation de la construction créant le tabelau.
N'oubliez pas par précaution d'enregistrer votre figure.
Une remarque : une fois la figure finie on peut supprimer les macro constructions qu'elle contient pour la rendre plus légère. Il faut pour cela utiliser l'outil ![]() puis l'item Supprimer une construction de la figure.
puis l'item Supprimer une construction de la figure.
Etape 2 : Création de notre ressource dans LaboMep
Connectez vous à LaboMep avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).
Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez par exemple Etude de variations de f avec f(x)=(ax+b)e^(-x).
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez la case première et terminale.
Dans les champs Résumé et Description, entrez f est la fonction définie par f(x)=(ax+b)e^(-x). Demande d'abord de calculer la dérivée de f puis de justifier son signe et enfin de compléter son tableau des variations..
En bas de la page, cliquez sur Créer la ressource.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour J3P.
Ensuite faites glisser Exercice de calcul multi-éditeurs et multi-étapes dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ Titre entrez ce qui suit :
Etude des variations de f avec f(x)=(ax+b)e^(-x)
Dans le champ nbrepetitions entrez la valeur 1.
Ouvrez la figure principale depuis l'endroit où vous l'aviez sauvegardée et utilisez l'icône ![]() d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
Collez ce code Base 64 dans le champ fig après avoir cliqué sur le bouton Saisie brute.
Dans les champs width et height entrez les valeurs que vous avez notées pour encadrer le tableau (dans notre exemple 515 et 220).
Dans le champ Param entrez ab (nous donnons à l'utilisateur la possibilité d'imposer les valeurs de a ou b).
Dans le champ nbEssais1 entrez 6 : l'élève aura 6 chances pour calculer la dérivée en fournissant une forme factorisée que nous acceptons comme finale.
Dans le champ nbEssais2 entrez 1 : On ne laisse qu'une chance pour justifier le signe de la dérivée.
Dans le champ coefEtape1, entrez 0.4 (nous donnons un peu plus d'importance pour le score au calcul de la dérivée). Il restera un coefficient de 0.4 pour la résolution de l'inéquation.
Dans les champs charset1, charset2 et charset3, entrez :
\dlnexp+-*/^²().,
Il s'agit des caractères au clavier permis lors des étapes 1, 2 et 3, \d désignant tous les chiffres.
Pour les boutons disponibles dans les éditeurs de formules, cochez les cases btnFrac (le bouton fraction), btnPuis (puissance), btnExp et btnLn et décochez toutes les autres cases correspondants aux autres boutons.
Validez les autres paramètres tel quels.
Dans l'éditeur de graphe, cliquez droit sur le nœud principal et renommez-le par exemple Variations de f avec f(x)=(ax+b)e^(-x).
Cliquez ensuite en bas sur le bouton Enregistrer pour sauvegarder votre ressource.
Vous pouvez maintenant tester votre ressource.
Si quelque chose ne fonctionne pas bien il faudra reprendre la figure MathGraph32, la corriger et modifier le paramètre fig de la figure.