Table des matières
MathGraph : exercice de calcul géométrique avec possibilité de tester des égalités intermédiaires
Nous désirons créer une ressource qu va demander à l'élève de calculer une longueur en utilisant le théorème de Pythagore avec la possibilité de tester des égalités intermédiaires avant de répondre, analogue à cette ressource : https://bibliotheque.sesamath.net/public/voir/612c79fe02b9ec76670f051f
Vous devrez pour cela utiliser la version JavaScript de MathGraph32, version 7.7.1 ou ultérieure, ou utiliser la version en ligne sur le site de MathGraph32.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
Pour vous aider à faire cette figure vous allez utiliser un macro construction.
Auparavant vous devez télécharger le fichier zip ci-dessous et décompresser son contenu dans le dossier de votre choix.
aideexerciceaveccalcuintermediaire.zip
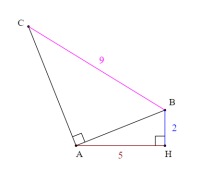
Notre but est de donner à l'élève une figure analogue à la figure ci-dessous et de lui demander de calculer la longueur AC. Les données de la figure devront être aléatoires.
Etape 1 : Création de la figure MathGraph
Commencez par créer la figure mathgraph.
Si vous désirez sauter ce qui suit vous pouvez utiliser le code Base 64 de la figure ci-dessous et, dans MathGraph32, utiliser l'icône ![]() puis choisir Figure par code Base 64.
puis choisir Figure par code Base 64.
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcvb6#gEA#wEAAAAAAAAAAAUeAAACygAAAQEAAAAAAAAAAQAAAGL#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAKQ1BvaW50QmFzZQD#####AAAAAAEOAAFVAMAkAAAAAAAAQBAAAAAAAAAAAAUAAEAwXfO2RaHKQDBd87ZFocr#####AAAAAQAUQ0Ryb2l0ZURpcmVjdGlvbkZpeGUA#####wEAAAAAEAAAAQAAAAEAAAABAT#wAAAAAAAA#####wAAAAEAD0NQb2ludExpZURyb2l0ZQD#####AAAAAAEOAAFWAMAAAAAAAAAAQBAAAAAAAAAAAAUAAUA9ogxJul42AAAAAv####8AAAABAAhDU2VnbWVudAD#####AAAAAAAQAAABAAAAAQAAAAEAAAAD#####wAAAAEAB0NNaWxpZXUA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAAQAAAAP#####AAAAAgAMQ0NvbW1lbnRhaXJlAP####8AAAAAAAAAAAAAAAAAQBgAAAAAAAAAAAAAAAUMAAAAAAABAAAAAAAAAAEAAAAAAAAAAAAEMSBjbf####8AAAABAAlDTG9uZ3VldXIA#####wAAAAEAAAAD#####wAAAAEAB0NDYWxjdWwA#####wAFbmJ2YXIAATMAAAABQAgAAAAAAAAAAAAJAP####8ABm5iY2FzMQABNAAAAAFAEAAAAAAAAAAAAAkA#####wAGbmJjYXMyAAE0AAAAAUAQAAAAAAAAAAAACQD#####AAZuYmNhczMAATMAAAABQAgAAAAAAAAAAAAJAP####8AAnIxABNpbnQocmFuZCgwKSpuYmNhczEp#####wAAAAIACUNGb25jdGlvbgL#####AAAAAQAKQ09wZXJhdGlvbgIAAAAKEQAAAAEAAAAAAAAAAD#vlv4nnz6s#####wAAAAEAD0NSZXN1bHRhdFZhbGV1cgAAAAkAAAAJAP####8AAnIyABNpbnQocmFuZCgwKSpuYmNhczIpAAAACgIAAAALAgAAAAoRAAAAAQAAAAAAAAAAP+xeLvv#VBYAAAAMAAAACgAAAAkA#####wACcjMAE2ludChyYW5kKDApKm5iY2FzMykAAAAKAgAAAAsCAAAAChEAAAABAAAAAAAAAAA#7ssGegeuigAAAAwAAAALAAAACQD#####AAFhAAQyK3IxAAAACwAAAAABQAAAAAAAAAAAAAAMAAAADAAAAAkA#####wACYicABDIrcjIAAAALAAAAAAFAAAAAAAAAAAAAAAwAAAANAAAACQD#####AAFiAB5zaShiJz1hLGErMStpbnQocmFuZCgwKSoyKSxiJyn#####AAAAAQANQ0ZvbmN0aW9uM1ZhcgAAAAALCAAAAAwAAAAQAAAADAAAAA8AAAALAAAAAAsAAAAADAAAAA8AAAABP#AAAAAAAAAAAAAKAgAAAAsCAAAAChEAAAABAAAAAAAAAAA#79RXeoL9bAAAAAFAAAAAAAAAAAAAAAwAAAAQAAAACQD#####AAFjABdpbnQoc3FydChhXjIrYl4yKSsyK3IzKQAAAAoCAAAACwAAAAALAAAAAAoBAAAACwD#####AAAAAQAKQ1B1aXNzYW5jZQAAAAwAAAAPAAAAAUAAAAAAAAAAAAAADgAAAAwAAAARAAAAAUAAAAAAAAAAAAAAAUAAAAAAAAAAAAAADAAAAA4AAAACAP####8AAAAAABAAAUEAAAAAAAAAAABACAAAAAAAAAAABQABQG0gAAAAAABAcTrhR64UewAAAAMA#####wEAAAABEAAAAQAAAAEAAAATAT#wAAAAAAAA#####wAAAAIACUNDZXJjbGVPUgD#####AQAAAAAAAAEAAAATAAAADAAAABEA#####wAAAAEAEENJbnREcm9pdGVDZXJjbGUA#####wAAABQAAAAV#####wAAAAEAEENQb2ludExpZUJpcG9pbnQA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAgAAABYAAAARAP####8AAAAAABAAAUgAAAAAAAAAAABACAAAAAAAAAAABQABAAAAFgAAAAUA#####wB#AAAAEAAAAQAAAAEAAAATAAAAGP####8AAAABABZDRHJvaXRlUGVycGVuZGljdWxhaXJlAP####8BAAAAABAAAAEAAAABAAAAGAAAABkAAAAPAP####8BAAAAAAAAAQAAABgAAAAMAAAADwAAAAAQAP####8AAAAaAAAAGwAAABEA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAQAAABwAAAARAP####8AAAAAABAAAUIAQBwAAAAAAADAOAAAAAAAAAAABQACAAAAHAAAAAUA#####wAAAP8AEAAAAQAAAAEAAAAYAAAAHgAAAAUA#####wAAAAAAEAAAAQAAAAEAAAATAAAAHgAAABIA#####wEAAAAAEAAAAQAAAAEAAAATAAAAIAAAAA8A#####wEAAAAAAAABAAAAHgAAAAwAAAASAAAAABAA#####wAAACEAAAAiAAAAEQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABAAAAIwAAABEA#####wAAAAAAEAABQwDAMgAAAAAAAMAxAAAAAAAAAAAFAAIAAAAjAAAABQD#####AAAAAAAQAAABAAAAAQAAABMAAAAlAAAABQD#####AP8A#wAQAAABAAAAAQAAAB4AAAAl#####wAAAAIAF0NNYXJxdWVBbmdsZUdlb21ldHJpcXVlAP####8AAAAAAAAAAQAAAAFAMAAAAAAAAAAAABMAAAAYAAAAHgAAABMA#####wAAAAAAAAABAAAAAUAwAAAAAAAAAAAAHgAAABMAAAAl#####wAAAAEAFENJbXBsZW1lbnRhdGlvblByb3RvAP####8AEk1lc3VyZSBkZSBsb25ndWV1cgAAAAUAAAACAAAAAgAAABMAAAAY#####wAAAAEAC0NNZWRpYXRyaWNlAAAAACoBAAAAABAAAAEAAAABAAAAEwAAABgAAAAGAAAAACoBAAAAABAAAAEAAAUAAAAAEwAAABgAAAAPAAAAACoBAAAAAAAAAQAAACwAAAABQDAAAAAAAAABAAAAEAAAAAAqAAAAKwAAAC0AAAARAAAAACoBAAAAABAAAAEAAAUAAQAAAC4AAAAIAQAAACoAAAATAAAAGP####8AAAABAA9DVmFsZXVyQWZmaWNoZWUBAAAAKgB#AAABAAAAAAAvEQAAAAAAAQAAAAEAAAABAAAAAAAAAAAAAAAAAQAAADAAAAAUAP####8AEk1lc3VyZSBkZSBsb25ndWV1cgAAAAUAAAACAAAAAgAAABgAAAAeAAAAFQAAAAAyAQAAAAAQAAABAAAAAQAAABgAAAAeAAAABgAAAAAyAQAAAAAQAAABAAAFAAAAABgAAAAeAAAADwAAAAAyAQAAAAAAAAEAAAA0AAAAAUAwAAAAAAAAAQAAABAAAAAAMgAAADMAAAA1AAAAEQAAAAAyAQAAAAAQAAABAAAFAAEAAAA2AAAACAEAAAAyAAAAGAAAAB4AAAAWAQAAADIAAAD#AQAAAAAANxEAAAAAAAEAAAABAAAAAQAAAAAAAAAAAAAAAAEAAAA4AAAAFAD#####ABJNZXN1cmUgZGUgbG9uZ3VldXIAAAAFAAAAAgAAAAIAAAAeAAAAJQAAABUAAAAAOgEAAAAAEAAAAQAAAAEAAAAeAAAAJQAAAAYAAAAAOgEAAAAAEAAAAQAABQAAAAAeAAAAJQAAAA8AAAAAOgEAAAAAAAABAAAAPAAAAAFAMAAAAAAAAAEAAAAQAAAAADoAAAA7AAAAPQAAABEAAAAAOgEAAAAAEAAAAQAABQABAAAAPgAAAAgBAAAAOgAAAB4AAAAlAAAAFgEAAAA6AP8A#wEAAAAAAD8RAAAAAAABAAAAAQAAAAEAAAAAAAAAAAAAAAABAAAAQAAAAAgA#####wAAABMAAAAeAAAACAD#####AAAAEwAAACUAAAAIAP####8AAAAYAAAAJQAAAAkA#####wAEcmVwMQABMAAAAAEAAAAAAAAAAP####8AAAABAAVDRm9uYwD#####AAR6ZXJvABJhYnMoeCk8MC4wMDAwMDAwMDEAAAALBAAAAAoA#####wAAAAIAEUNWYXJpYWJsZUZvcm1lbGxlAAAAAAAAAAE+ES4L6CbWlQABeAAAAAkA#####wAFbG9uZzIAC2NeMi1hXjItYl4yAAAACwEAAAALAQAAAA4AAAAMAAAAEgAAAAFAAAAAAAAAAAAAAA4AAAAMAAAADwAAAAFAAAAAAAAAAAAAAA4AAAAMAAAAEQAAAAFAAAAAAAAAAAAAAAkA#####wABawAQZGl2bWF4cChsb25nMiwyKf####8AAAABAA1DRm9uY3Rpb24yVmFyCAAAAAwAAABHAAAAAUAAAAAAAAAAAAAACQD#####AAFxAAlsb25nMi9rXjIAAAALAwAAAAwAAABHAAAADgAAAAwAAABIAAAAAUAAAAAAAAAAAAAACQD#####AAZxZWdhbDEACXplcm8ocS0xKf####8AAAABAA5DQXBwZWxGb25jdGlvbgAAAEYAAAALAQAAAAwAAABJAAAAAT#wAAAAAAAAAAAACQD#####AAVrZGlmMQAHMS0oaz0xKQAAAAsBAAAAAT#wAAAAAAAAAAAACwgAAAAMAAAASAAAAAE#8AAAAAAAAAAAAAkA#####wAEc29sMQALc3FydChsb25nMikAAAAKAQAAAAwAAABHAAAACQD#####AARzb2wyAAlrKnNxcnQocSkAAAALAgAAAAwAAABIAAAACgEAAAAMAAAASQAAAAkA#####wAFc29sJzIAAWsAAAAMAAAASP####8AAAAEABBDVGVzdEVxdWl2YWxlbmNlAP####8ABHRlcTEAAABMAAAARQEAAAAAAT#wAAAAAAAAAQEBAAAAGwD#####AAR0ZXEyAAAATQAAAEUBAAAAAAE#8AAAAAAAAAEBAQAAABsA#####wAFdGVxJzIAAABOAAAARQEAAAAAAT#wAAAAAAAAAQEBAAAACQD#####AAdyZXNvbHUxAClzaShxZWdhbDEsdGVxJzIsc2koa2RpZjEsdGVxMXx0ZXEyLHRlcTEpKQAAAA0AAAAADAAAAEoAAAAMAAAAUQAAAA0AAAAADAAAAEsAAAALCwAAAAwAAABPAAAADAAAAFAAAAAMAAAATwAAAAkA#####wAGaW50ZXJtAAEwAAAAAQAAAAAAAAAAAAAACQD#####AAR2cmFpACJ6ZXJvKGdhdWNoZShpbnRlcm0pLWRyb2l0KGludGVybSkpAAAAGgAAAEYAAAALAQAAAAoUAAAADAAAAFMAAAAKFQAAAAwAAABT#####wAAAAIABkNMYXRleAD#####AQAAAAEAAP####8QQHzwAAAAAABAWuuFHrhR7AAAAAAAAAAAAAAAAAABAAAAAAAAAAAAbFxJZntxZWdhbDF9CnsKXG1hdGhybXtBQ30gPSBcRm9yU2ltcHtzb2wnMn0KfQp7ClxtYXRocm17QUN9ID0gXEZvclNpbXB7c29sMX0gXElme2tkaWYxfXs9XEZvclNpbXB7c29sMn19e30Kff####8AAAABABBDTWFjcm9BcHBhcml0aW9uAP####8BAAD#AQAA#####xBAfNAAAAAAAEBn1cKPXCj2AgH###8AAAAAAAAAAAAAAAEAAAAAAAAAAAAIc29sdXRpb24AAAAAAAEAAABVAAAAABwA#####wEAAP8BAAZpbnRlcm3#####EEB80AAAAAAAQG91wo9cKPYAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAxcRm9ye2ludGVybX0AAAAcAP####8BAAAAAQAGZW5vbmNl#####xBAf5AAAAAAAEA71wo9cKPgAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAENXGJlZ2lue2FycmF5fXtsfQpcdGV4dHtPbiBjb25zaWTDqHJlIGxhIGZpZ3VyZSBjaS1kZXNzb3VzLCBvw7kgQUhCIGVzdCB1biB0cmlhbmdsZSByZWN0YW5nbGUgZW4gSCwgYXZlY30gClxcIFx0ZXh0e0hCID0gJFxWYWx7YX0kLCBIQSA9ICRcVmFse2J9JCBldCBCQUMgZXN0IHVuIHRyaWFuZ2xlIHJlY3RhbmdsZSBlbiBBIHRlbCBxdWUgQkMgPSAkXFZhbHtjfSQufQpcXCBcdGV4dHtMZSBidXQgZXN0IGRlIGNhbGN1bGVyIGxhIGxvbmd1ZXVyIEFDLn0KXGVuZHthcnJheX0AAAAcAP####8BAAAAAQALZW5vbmNlU3VpdGX#####EEB#cAAAAAAAQGIa4UeuFHsAAAAAAAAAAAAAAAAAAQAAAAAAAAAAADFcdGV4dHtJbCBmYXV0IG1haW50ZW5hbnQgZG9ubmVyIGxhIHZhbGV1ciBkZSBBQy59AAAAHAD#####AQAAAAEAC2Zvcm11bGFpcmUy#####xBAf2AAAAAAAEBleuFHrhR7AAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAUXHRleHR7QUMgPSBlZGl0MSBjbX0AAAAJAP####8ABGZvcjEAB2JeMithXjIAAAALAAAAAA4AAAAMAAAAEQAAAAFAAAAAAAAAAAAAAA4AAAAMAAAADwAAAAFAAAAAAAAAAAAAAAkA#####wAEZm9yMgAIY14yLWZvcjEAAAALAQAAAA4AAAAMAAAAEgAAAAFAAAAAAAAAAAAAAAwAAABbAAAACQD#####AAJjMgADY14yAAAADgAAAAwAAAASAAAAAUAAAAAAAAAAAAAACQD#####AARmb3IzAAdjMi1mb3IxAAAACwEAAAAMAAAAXQAAAAwAAABbAAAACQD#####AAJrMgADa14yAAAADgAAAAwAAABIAAAAAUAAAAAAAAAAAAAACQD#####AARmb3I0ABtzcXJ0KGsyKnEpPXNxcnQoazIpKnNxcnQocSkAAAALCAAAAAoBAAAACwIAAAAMAAAAXwAAAAwAAABJAAAACwIAAAAKAQAAAAwAAABfAAAACgEAAAAMAAAASQAAABwA#####wEAAAABAAhzb2x1dGlvbv####8QQH9QAAAAAABAaLrhR64UfAAAAAAAAAAAAAAAAAABAAAAAAAAAAACR1xiZWdpbnthcnJheX17bH0KXHRleHR7RW4gYXBwbGlxdWFudCBsZSB0aMOpb3LDqG1lIGRlIFB5dGhhZ29yZSBkYW5zIGxlIHRyaWFuZ2xlIEFIQiByZWN0YW5nbGUgZW4gSCA6fQpcXCBcdGV4dHskXG1hdGhybXtIQX3CsiArIFxtYXRocm17SEJ9wrIgPSBcbWF0aHJte0FCfcKyJCBkb25jICRcbWF0aHJte0FCfcKyPVxGb3JTaW1we2ZvcjF9PVxWYWx7Zm9yMX0kfQpcXCBcdGV4dHtEYW5zIGxlIHRyaWFuZ2xlIEJBQyByZWN0YW5nbGUgZW4gQSA6fQpcXCBcdGV4dHskXG1hdGhybXtBQn3CsiArIFxtYXRocm17QUN9wrIgPSBcbWF0aHJte0JDfcKyJCBkb25jICRcbWF0aHJte0FDfcKyPVxtYXRocm17QkN9wrItXG1hdGhybXtBQn3Csj1cRm9yU2ltcHtmb3IyfSR9ClxcIFx0ZXh0eyRcbWF0aHJte0FDfcKyPVxGb3JTaW1we2ZvcjN9PVxWYWx7bG9uZzJ9JH0KXFwgXHRleHR7CmQnb8O5ICRcbWF0aHJte0FDfT1cRm9yU2ltcHtzb2wxfSQKXElme3FlZ2FsMX17PVxWYWx7a319ewpcSWZ7a2RpZjF9eyBvdSBlbmNvcmUgJFxtYXRocm17QUN9PVxGb3JTaW1we2ZvcjR9PVxGb3JTaW1we3NvbDJ9JH17fQp9Cn0KXGVuZHthcnJheX0AAAAH##########8=
Sinon :
Dans MathGraph32, utilisez l'icône  de création d'une nouvelle figure et cliquez sur l'item Figure sans repère et avec longueur unité.
de création d'une nouvelle figure et cliquez sur l'item Figure sans repère et avec longueur unité.
Pour éviter que la figure obtenue ne soit trop grande pour LaboMep, utilisez l'icône d'options ![]() de la barre d'outils supérieure et cochez la case Utiliser un cadre de dimensions données puis entrez 700 et 350 dans les champs Largeur et hauteur puis validez. Un cadre grisé apparaît. Vous devrez prendre garde que tous les éléments créés restent bien dans ce cadre.
de la barre d'outils supérieure et cochez la case Utiliser un cadre de dimensions données puis entrez 700 et 350 dans les champs Largeur et hauteur puis validez. Un cadre grisé apparaît. Vous devrez prendre garde que tous les éléments créés restent bien dans ce cadre.
Pour pouvoir utiliser une des macro constructions téléchargées dans MathGraph32, cliquez d'abord sur l'icône ![]() qui fait apparaître des icônes supplémentaires.
qui fait apparaître des icônes supplémentaires.
Cliquez ensuite sur l'icône ![]() (gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
(gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
Allez dans le dossier où vous avez décompressé le fichier zip contenant les constructions et cliquez sur le fichier nommé aideInterm3ValeursAleat.mgc puis validez.
Pour être implémentée, notre construction a besoin d'un calcul provisoire.
Déroulez la barre des calculs et cliquez sur l'icône ![]() . Créez un calcul nommé calcmac avec comme formule 0 (la formule de calcmac n'a pas d'importance).
. Créez un calcul nommé calcmac avec comme formule 0 (la formule de calcmac n'a pas d'importance).
Utilisez l'icône l'icône ![]() et cliquez sur Implémenter une construction de la figure.
et cliquez sur Implémenter une construction de la figure.
La seule macro présente est déjà sélectionnée comme ci-dessous.
Cliquez sur le bouton Implémenter.
Une autre boîte de dialogue apparaît vos demandant de choisir les objets sources pour implémenter cette macro. Un seul objet source est requis : ce sera notre calcul calcmac.
Dans la liste, affectez à l'objet source numéro 1 le calcul calcmac en le sélectionnant comme ci-dessous puis validez.
La construction est implémentée et a créé pour vous plusieurs objets :
- des calculs nommés nbvar, nbcas1, nbcas2, nbcas3, r1, r2, r3 : leur présence est nécessaire pour que, si on répète plusieurs fois la ressource, les donénes de l'exercice ne soient pas les mêmes.
- des calculs nommés interm et vrai : ils seront utilisés pour vérifier les calculs intermédiaires de l'élève et vous n'avez pas à vous en soucier.
- un affichage LaTeX caché de tag interm dont vous n'avez pas à vous soucier non plus mais sa présence est indispensable.
- une fonction de la variable x qui renvoie 1 quand la valeur absolue de x est inéférieure à 10^(-9) et 0 sinon.
- des affichages LaTeX pour fournir l'énoncé, la suite de l'énoncé à l'étape 2, le formulaire à l'étape 2 et la solution. Nous allons devoir ensuite les modifier.
Pour pouvoir modifier les objets finaux créés pas cette macro construction nous devons les transformer on objets normaux.
Pour cela, utilisez à nouveau l'icône ![]() (gestion des constructions) et cliquez sur l'item Fusionner les constructions de la figure.
(gestion des constructions) et cliquez sur l'item Fusionner les constructions de la figure.
Pour simplifier, nous garderons notre calcul calcmac mais il y a trois formules que nous devons absolument changer : les formules de nbcas1, nbcas2 et nbcas3
Dans la barre supérieure utilisez l'icône ![]() (modification d'objet numérique) et utilisez la boîte de dialogue pour changer les formules comme indiqué ci-dessous :
(modification d'objet numérique) et utilisez la boîte de dialogue pour changer les formules comme indiqué ci-dessous :
| Nom du calcul | Ancienne formule | Nouvelle formule | Commentaire |
|---|---|---|---|
| nbcas1 | calcmac | 4 | Ainsi r1 défini après par la formule int(rand(0)*nbcas1) pourra prendre les valeurs entières aléatoires de 0 à 3 |
| nbcas2 | calcmac | 4 | Ainsi r2 défini après pourra prendre les valeurs entières aléatoires de 0 à 3 |
| nbcas3 | calcmac | 4 | Ainsi r3 défini après pourra prendre les valeurs entières aléatoires de 0 à 3 |
Refermez la boîte de dialogue.
A l'aide de l'outil ![]() de la barre supérieure, cliquez sur les points U et V et cochez la case Nom masqué avant de valider.
de la barre supérieure, cliquez sur les points U et V et cochez la case Nom masqué avant de valider.
A l'aide de l'outil ![]() de la barre supérieure, cliquez sur l'affichage de texte situé sous le segment [UV] et, dans la champ Texte à afficher, entrez 1 cm au lieu de 1.
de la barre supérieure, cliquez sur l'affichage de texte situé sous le segment [UV] et, dans la champ Texte à afficher, entrez 1 cm au lieu de 1.
Déroulez la barre d'outil des calculs et utilisez l'icône  pour créer les calculs suivants :
pour créer les calculs suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| a | 2+r1 | a contiendra un entier aléatoire entre 2 et 5 |
| b' | 2+r2 | b' contiendra un entier aléatoire entre 2 et 5 |
| b | si(b'=a,a+1,b') | b sera ainsi différent de a et le triangle ne sera jamais isocèle |
| c | int(sqrt(a^2+b^2)+2+r3) | Fournira la longueur du segment sur la figure (nombre entier) |
Nous allons maintenant modifier l'affichage LaTeX qui fournira à l'exercice l'énonce de cet exercice. La macro construction a affecté à cet affichage LaTeX un tag enonce ce qui permettra à LaboMep de le reconnaître comme tel.
Comme cet affichage LaTeX doit utiliser des objets que nous avons créés après avoir implémenté la macro construction, nous allons d'abord reclasser cet affichage LaTeX vers la fin de la liste des objets créés.
Utilisez pour cela l'outil ![]() puis cliquez sur l'affichage LaTeX d'énoncé créé par la macro construction.
puis cliquez sur l'affichage LaTeX d'énoncé créé par la macro construction.
Utilisez maintenant l'icône ![]() (modification d'objet graphique dans la barre d'outils des affichages) puis cliquez en haut et à droite de la figure).
(modification d'objet graphique dans la barre d'outils des affichages) puis cliquez en haut et à droite de la figure).
Dans la boîte de dialogue qui s'ouvre remplacez dans le champ d'édition le code LaTeX par le Code LaTeX suivant (vous pouvez utiliser les boutons ![]() et Insertion de valeur pour accélérer le processus :
et Insertion de valeur pour accélérer le processus :
\begin{array}{l}
\text{On considère la figure ci-dessous, où AHB est un triangle rectangle en H, avec}
\\ \text{HB = $\Val{a}$, HA = $\Val{b}$ et BAC est un triangle rectangle en A tel que BC = $\Val{c}$.}
\\ \text{Le but est de calculer la longueur AC.}
\end{array}
Le contenu de chaque \text du code LaTeX ci-dessus sera récupéré pour afficher une ligne de la consigne.
Maintenant masquez cet affichage LaTex avec l'outil ![]() de la barre d'outils supérieure. Il ne doit pas être visible dans la figure.
de la barre d'outils supérieure. Il ne doit pas être visible dans la figure.
Avec l'outil ![]() , créez un point libre et nommez-le A (on peut déplacer le nom des points avec l'outil
, créez un point libre et nommez-le A (on peut déplacer le nom des points avec l'outil ![]() ).
).
Avec l'outil ![]() , créez une droite horizontale passant par A.
, créez une droite horizontale passant par A.
Avec l'outil ![]() , créez le cercle de centre A et de rayon b.
, créez le cercle de centre A et de rayon b.
Avec l'outil ![]() , créez l'intersection de ce cercle avec la droite horizontale et nommer H le point qui est situé à droite de A.
, créez l'intersection de ce cercle avec la droite horizontale et nommer H le point qui est situé à droite de A.
Maintenant, avec l'icône ![]() de la barre d'outils horizontale, masquer la droite horizontale et le cercle ainsi que le point d'intersection autre que H.
de la barre d'outils horizontale, masquer la droite horizontale et le cercle ainsi que le point d'intersection autre que H.
Créez avec l'outil ![]() le segment [AH].
le segment [AH].
Avec l'outil ![]() , créez la droite perpendiculaire au segment [AH] passant par H (cliquer d'abord sur le segment puis sur le point H).
, créez la droite perpendiculaire au segment [AH] passant par H (cliquer d'abord sur le segment puis sur le point H).
Avec l'outil ![]() , créez le cercle de centre H et de rayon a.
, créez le cercle de centre H et de rayon a.
Avec l'outil ![]() , créez l'intersection de ce cercle avec la droite perpendiculaire et nommez B le point qui est situé au-dessus du segment [AH].
, créez l'intersection de ce cercle avec la droite perpendiculaire et nommez B le point qui est situé au-dessus du segment [AH].
Créez maintenant les segments [AB] et [HB] et masquez le cercle, la perpendiculaire et le deuxième point d'intersection.
Avec l'outil ![]() , créez la droite perpendiculaire au segment [AB] passant par A.
, créez la droite perpendiculaire au segment [AB] passant par A.
Avec l'outil ![]() , créez le cercle de centre B et de rayon c.
, créez le cercle de centre B et de rayon c.
Avec l'outil ![]() , créez l'intersection de ce cercle avec la droite perpendiculaire en A et nommer C le point qui est situé au-dessus du segment [AB].
, créez l'intersection de ce cercle avec la droite perpendiculaire en A et nommer C le point qui est situé au-dessus du segment [AB].
Créez maintenant les segments [AC] et [BC] et masquez le cercle, la perpendiculaire et le deuxième point d'intersection.
Nous allons maintenant créer une marque d'angle pour l'angle H. Pour cela dérouler la barre des icônes de marques et activer l'outil ![]() puis cliquer dans cet ordre sur A, H et B.
puis cliquer dans cet ordre sur A, H et B.
Procédez de même pour créer une marque de l'angle BAC.
Nous voulons maintenant afficher les longueurs des segments [AH], [BH] et [BC] sur la figure.
Pour cela, vérifiez d'abord avec l'outil ![]() de la barre d'outils horizontale (options de la figure) que la case Affichage automatique des mesures de longueur et angle est cochée.
de la barre d'outils horizontale (options de la figure) que la case Affichage automatique des mesures de longueur et angle est cochée.
Dans la palette des couleurs à droite, sélectionnez la couleur marron,cliquez sur l'icône ![]() puis cliquez sur A et H. La mesure apparaît sous le segment.
puis cliquez sur A et H. La mesure apparaît sous le segment.
Procédez de même pour mesurer et afficher les mesures de longueurs des segments [BH] (en bleu) et [BC] (en magenta).
Maintenant, avec l'outil ![]() de la barre d'outils horizontale (options de la figure) décochez la case Affichage automatique des mesures de longueur et angle.
de la barre d'outils horizontale (options de la figure) décochez la case Affichage automatique des mesures de longueur et angle.
Pour que l'élève puisse dans ses calculs intermédiaires, utiliser des longueurs, celles-ci doivent être présente dans notre figure Mathgraph32.
Ainsi, créez avec l'outil ![]() la mesure des longueurs des segments [AB], [AC] et [HC].
la mesure des longueurs des segments [AB], [AC] et [HC].
Il faut noter que ces trois dernières longueurs existent comme objets numériques mais ne sont pas visibles sur la figure. Vous pouvez le voir avec l'outil ![]() de la barre d'outils supérieure.
de la barre d'outils supérieure.
Maintenant, pour une meilleure unité graphique de la figure, nous allons utiliser l'outil ![]() (palette) pour donner aux segments [AH], [HB] et [BC] respectivement la couleur marron, bleue et magenta (cliquer sur la couleur dans la palette de couleurs avant de cliquer sur l'objet. Cet outil donne aussi aux objets le style de trait actif (qui doit être ici le style de trait continu).
(palette) pour donner aux segments [AH], [HB] et [BC] respectivement la couleur marron, bleue et magenta (cliquer sur la couleur dans la palette de couleurs avant de cliquer sur l'objet. Cet outil donne aussi aux objets le style de trait actif (qui doit être ici le style de trait continu).
Nous devons maintenant préparer les objets numériques qui serviront à vérifier la validité de la réponse de l'élève.
Dans la réponse finale attendue de la part de l'élève, nous n'attendons qu'un seul résultat qui est est la valeur exacte de la longueur AC.
Notre figure devra donc contenir :
- Un calcul nommé rep1 contenant la réponse de l'élève.
- Un calcul nommé exact1 contenant 1 si la réponse de l'élève est exacte.
- Un calcul nommé resolu1 contenant 1 si la réponse entrée par l'élève est une des réponses que nous acceptons comme réponse finale et 0 sinon.
En déroulant la barre d'outils des objets numériques, activez l'outil ![]() de création d'un calcul réel et créez un calcul nommé rep1 avec comme formule 0.
de création d'un calcul réel et créez un calcul nommé rep1 avec comme formule 0.
Créez un calcul réel nommé long2 avec comme formule :
c^2-a^2-b^2
puis un calcul nommé sol1 avec comme formule :
sqrt(long2)
Conformément aux programmes de collège nous accepterons une réponse équivalent à sol1 comme réponse finale sauf si la racine carrée a pour résultat un nombre entier.
Mais nous devons aussi accepter une réponse où l'élève aura extrait le plus grand entier possible de la racine carrée (si c'est possible).
Créez de nouveaux calculs réels :
| Nom du calcul | Formule | Commentaire | |
|---|---|---|---|
| k | divmaxp(long2,2) | divmaxp(x, p) est une fonction prédéfinie de deux variables qui fournit le plus grand entier k strictement supérieur à 1 tel que k^p divise x | |
| q | long2/k | 2 | |
| qegal1 | zero(q-1) | On utilise la fonction zero (qui a été créé par la macro-construction) pour éviter les problèmes d'arrondi. qegal1 sera égal à 1 quand long2 est le carré de k | |
| kdif1 | 1-(k=1) | Sera égal à O si k égal 1 et 0 si k est différent de 1 | |
| sol2 | k*sqrt(q) | Une des formes possibles de la solution | |
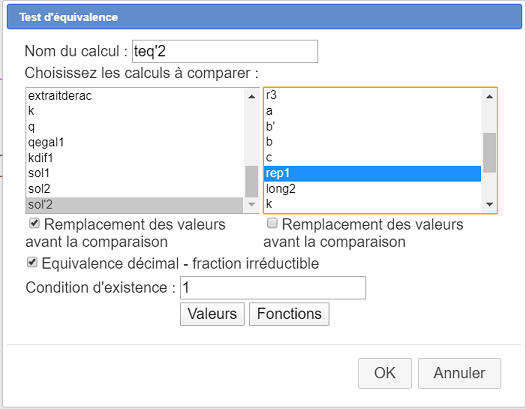
| sol'2 | k | Servia lors d'une test d'équivalence. Doit donc contenir la valeur de k mais sans aucun calcul | |
| exact1 | zero(rep1-sol1) | Vaudra 1 quand la réponse de l'élève est exacte (à 'epsilon près) mais n'est pas forcément la réponse finale | |
Pour déterminer si l'élève a donné une des réponses finales attendues, nous allons créer des tests d'équivalences.
La création d'un test d'équivalence se fait en déroulant la barre des icônes de calcul, en cliquant à sa droite sur l'icône ![]() et en choisissant Test d'équivalence dans la liste.
et en choisissant Test d'équivalence dans la liste.
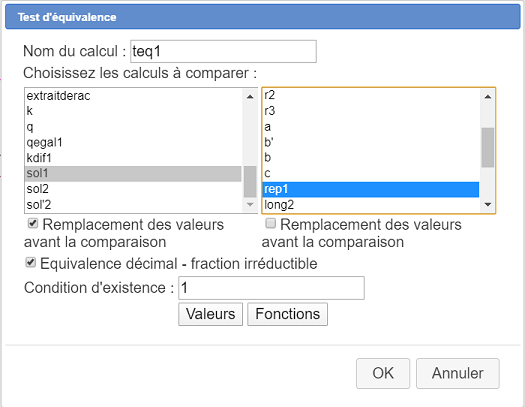
Commencez par un premier test d'équivalence nommé teq1 comme ci-dessous :
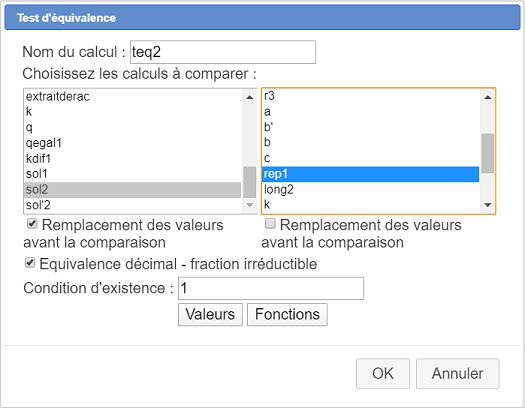
Puis un test d'équivalence nommé teq2 comme ci-dessous :
Enfin un test d'équivalence nommé teq'2 comme c–dessous :
Nous allons maintenant créer le calcul qui doit être nommé résolu1 (car associé à notre seul et unique éditeur de la question finale) chargé de dire si la réponse de l'élève est une des réponses finales acceptées.
Créez un nouveau calcul réel nommé resolu1 avec comme formule :
si(qegal1,teq'2,si(kdif1,teq1|teq2,teq1))
Dans notre exemple, nous afficherons lors de la correction la formule finale donnant la réponse pour la longueur AC.
Déroulez la barre des outils d'affichage et cliquez sur l'icône ![]() .
.
Cliquez à droite de la figure pour désigner le futur emplacement de notre affichage LaTeX.
Dans la boîte de dialogue qui s'ouvre, entrez dans le champ Code LaTeX le code suivant :
\If{qegal1}
{
\mathrm{AC} = \ForSimp{sol'2}
}
{
\mathrm{AC} = \ForSimp{sol1} \If{kdif1}{=\ForSimp{sol2}}{}
}
Ce code LaTeX comprend des affichages LaTeX conditionnels qui sont spécifiques à MathGraph32.
Vous pouvez cliquer plusieurs fois sur l'icône ![]() qui relance les calculs aléatoires de la figure pour voir ce que donne nogtre affichage.
qui relance les calculs aléatoires de la figure pour voir ce que donne nogtre affichage.
Cet affichage LaTeX ne devra être visible que lors de la phase de correction.
Pour cela nous devons créer une macro d'apparition d'objet dont l'intitulé est solution.
Pour créer cette macro, déroulez la barre des outils d'affichages et cliquez sur l'icône ![]() .
.
Dans la liste proposée, cliquez sur Macro d'apparition et validez.
Cliquez à l'endroit d'affichage de la macro, par exemple au-dessous du dernier affichage LaTeX déjà présent en bas et à droite.
Il vous en ensuite demandé de cliquer sur les objets que la macro doit faire apparaitre.
Cliquez sur l'affichage LaTeX puis cliquez sur le bouton rouge STOP en bas et à droite pour dire que vous avez désigné tous les objets. L'intitulé de la macro apparaît.
Il nous reste à masquer notre affichage LaTeX et la mcro en utilisant l'outil ![]() : cliquez sur l'affichage LaTeX et la macro pour les masquer.
: cliquez sur l'affichage LaTeX et la macro pour les masquer.
Cette macro sera automatiquement exécutée lors de la correction.
Nous allons maintenant créer des calculs qui serviront à l'affichage LaTeX de la solution.
Créez les calculs réels suivants (avec l'outil ![]() :
:
| Nom du calcul | Formule | ||
|---|---|---|---|
| for1 | b | 2+a | 2 |
| for2 | c | 2-for1 | |
| c2 | c | 2 | |
| for3 | c2-for1 | ||
| k2 | k | 2 | |
| for4 | sqrt(k2*q)=sqrt(k2)*sqrt(q) |
Nous devons maintenant créer modifier les trois affichages LaTeX restants qui ont été créés par la macro construction.
Utilisez l'icône ![]() et cliquez sur l'affichage LaTeX fournissant la suite de l'énoncé.
et cliquez sur l'affichage LaTeX fournissant la suite de l'énoncé.
Remplacez son code LaTeX par le code LaTeX ci-dessous :
\text{Il faut maintenant donner la valeur de AC.}
Lorsque l'élève cliquera sur le bouton Passer à la réponse finale on lui affichera donc le message : Il faut maintenant donner la valeur de AC.
A nouveau cliquez sur l'icône ![]() et modifiez l'affichage LaTeX contenant le formulaire pour la deuxième étape. Remplacez son code LaTeX par celui-ci :
et modifiez l'affichage LaTeX contenant le formulaire pour la deuxième étape. Remplacez son code LaTeX par celui-ci :
\text{AC = edit1 cm}
Lors de l'étape finale sera donc affiché AC = suivi d'un éditeur de formule repéré dans le code LaTeX par edit.
Enfin modifiez aussi l'affichage LaTeX créé par la construction destiné à fournir la solution à afficher.
Voici le code LaTeX à utiliser :
\begin{array}{l}
\text{En appliquant le théorème de Pythagore dans le triangle AHB rectangle en H :}
\\ \text{$\mathrm{HA}² + \mathrm{HB}² = \mathrm{AB}²$ donc $\mathrm{AB}²=\ForSimp{for1}=\Val{for1}$}
\\ \text{Dans le triangle BAC rectangle en A :}
\\ \text{$\mathrm{AB}² + \mathrm{AC}² = \mathrm{BC}²$ donc $\mathrm{AC}²=\mathrm{BC}²-\mathrm{AB}²=\ForSimp{for2}$}
\\ \text{$\mathrm{AC}²=\ForSimp{for3}=\Val{long2}$}
\\ \text{
d'où $\mathrm{AC}=\ForSimp{sol1}$
\If{qegal1}{=\Val{k}}{
\If{kdif1}{ ou encore $\mathrm{AC}=\ForSimp{for4}=\ForSimp{sol2}$}{}
}
}
\end{array}
Rappelons que le code LaTeX spécial MathGraph32 \ForSimp{calc} affiche le code LaTeX du calcul calc en remplaçant auparavant les calculs utilisés dans la formule de calc par leurs valeurs et en supprimant les additions de 0 et les produits par 1.
Pour que notre exercice fonctionne bien quand l'élève fait ses calculs intermédiaire, nous devons reclasser le calcul nommé interm qui a été créé par la macro construction le plus possible vers la liste des objets créés.
Pour cela utilisez l'outil ![]() , sélectionnez dans la liste le calcul nommé interm puis cliquez à droite sur l'icône
, sélectionnez dans la liste le calcul nommé interm puis cliquez à droite sur l'icône ![]() qui va reclasser ce calcul et les objets qui en dépendent en fin de liste.
qui va reclasser ce calcul et les objets qui en dépendent en fin de liste.
Il vous reste à utiliser l'outil ![]() pour masquer tous nos affichages LaTeX qui ne servent qu'à fournir des informations à LaboMep lors du déroulement de l'exercice.
pour masquer tous nos affichages LaTeX qui ne servent qu'à fournir des informations à LaboMep lors du déroulement de l'exercice.
Etape 2 : Création de notre ressource dans LaboMep
Connectez vous à LaboMep avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).
Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez par exemple Application double du théorème de Pythagore.
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez les cases seconde et troisième.
Dans les champs Résumé et Description, entrez Demande de calculer une longueur en appliquant deux fois le théorème de Pythagore.
En bas de la page, cliquez sur Créer la ressource.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour J3P.
Ensuite faites glisser Exercice de calcul multi éditeurs avec calculs intermédiaires dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ Titre entrez ce qui suit :
Calcul d'une longueur
Le champ fig doit contenir le code Base64 de la première figure que nous avons préparée.
Si nécessaire, rouvrez la figure et utilisez l'icône d'exportation ![]() de la barre d'outils supérieure et choisissez Obtenir le code Base64 de la figure. Si vous utilisez la version autonome de MathGraph32, un message vous prévient que le code Base 64 a été copié dans le presse-papier. Sinon une boîte de dialogue apparaît vous présentant ce code dans un champ d'édition dont vous devez copier le contenu dans le presse-papier.
de la barre d'outils supérieure et choisissez Obtenir le code Base64 de la figure. Si vous utilisez la version autonome de MathGraph32, un message vous prévient que le code Base 64 a été copié dans le presse-papier. Sinon une boîte de dialogue apparaît vous présentant ce code dans un champ d'édition dont vous devez copier le contenu dans le presse-papier.
Collez le contenu du presse-papier dans le champ fig (il s’agit d’une très grosse chaîne de caractères commençant par les caractères TWF0a). Cette chaîne a été fournie en haut de cet article.
Dans le champ width, entrez 700 (largeur de la figure)
Dans le champ height, entrez 350 (hauteur de la figure)
Dans le champ param, entrez abc. Cela permet à l'utilisateur d'imposer des valeurs aux calculs a, b et c.
Dans le champ nbEssais1 entrez 4 (ce sera le nombre d'égalités intermédiaires maximum que l'élève pourra tester avant de passer à la réponse finale).
Dans le champ nbEssais2, entrez par exemple 2 (ce sera le nombre maximum de réponses possibles à la réponse finale)
Laissez la case simplifier à true. Nous exigeons donc que la réponse finale soit une des réponses que nous avons choisi d'attendre, sinon n'importe quel calcul donnant la valeur de la longueur AC sera acceptée.
Dans le champ charset1 entrez : =;AHBC\d.,+\-/*²^ (\ est un raccourci pour avoir tous les chiffres)
Dans le champ charset2 entrez :
\d.,+\-/*²^
(dans la réponse finale on n'a plus besoin d'utiliser le nom des points).
A noter que si vous laissez charset1 et charset2 vides il n'y aura pas sur périphérique mobile de claver virtuel.
Dans le champ enonceSimplifier, entrez
Le résultat doit être donné sous la forme exacte la plus simple possible.
En bas de la boîte de dialogue, cliquez sur le bouton Valider.
En bas de la page, cliquez sur le bouton Enregistrer.
Si vous voulez maintenant tester votre ressource, fermez d’abord l’onglet Application double du théorème de Pythagore puis, dans Mes Ressources, faites un clic droit sur la ressource Application double du théorème de Pythagore et choisissez Tester la ressource.
Vous pouvez maintenant tester la ressource.
Récapitulatif des objets numériques créés
Calculs pour initialiser la figure
| Nom du calcul | Formule | Utilité |
|---|---|---|
| nbvar | 3 | nombre de paramètres aléatoires de notre exercice (créé par la maccro construction) |
| nbcas1 | 4 | en cas de répétition de l'exercice, des valeurs différentes des précédentes seront proposées (créé par la maccro construction) |
| r1 | int(rand(0)*nbcas1) | r1 pourra prendre 4 valeurs entières (de 0 à 3) (créé par la maccro construction) |
| nbcas2 | 4 | en cas de répétition de l'exercice, des valeurs différentes des précédentes seront proposées (créé par la maccro construction) |
| r2 | int(rand(0)*nbcas2) | r2 pourra prendre 4 valeurs entières (de 0 à 3). |
| nbcas3 | 4 | en cas de répétition de l'exercice, des valeurs différentes des précédentes seront proposées (créé par la maccro construction) |
| r3 | int(rand(0)*nbcas3) | r3 pourra prendre 4 valeurs entières (de 0 à 3) (créé par la maccro construction) |
| a | 2+r1 longueur | HB |
| b’ | 2+r2 | longueur HA |
| b | si(b'=a,a+1,b') | longueur HA (b sera différent de a et le triangle AHB ne sera pas rectangle isocèle) |
| c | int(sqrt(a^2+b^2)+2+r3) | longueur BC |
Fonctions d'utilité générale
| Nom de la fonction | Formule | Utilité |
|---|---|---|
| zero | abs(x)<0.000000001 | Renvoie 1 si la valeur absolue de l'argument est strictement inférieure à 10-9 (créé par la maccro construction) |
Calculs ou fonctions pour vérifier la réponse de l'élève
| Nom du calcul | Formule | Utilité |
|---|---|---|
| rep1 | 0 | Sera la formule correspondant à la réponse de l'élève |
| long2 | c^2-a^2-b^2 | Contient le carré de la longueur demandée |
| k | divmaxp(long2,2) | Plus grand nombre entier dont le carré divise long2 |
| q | long2/k^2 | quotient de long2 par k² |
| qegal1 | zero(q-1) | Vaut 1 si q est égal à 1 et 0 sinon |
| kdif1 | 1-(k=1) | Vaut 1 si k est différent de 1 et 0 sinon |
| sol1 | sqrt(long2) | Contient une des formules acceptées comme finale si la racine ne tombe pas juste |
| sol2 | k*sqrt(q) | Contient la formule avec carrée extraite aussi acceptée comme solution finale si k n'est pas égal à 1 |
| sol'2 | k | Contient la seule réponse accepté quand la racine carrée tombe juste pour le résultat |
| exact1 | zero(rep1-sol1) | 1 si la réponse de l'élève est exacte |
| teq1 | Test d'équivalence entre la réponse de l'élève et la solution sol1 | |
| teq2 | Test d'équivalence entre la réponse de l'élève et la solution sol2 | |
| teq'2 | Test d'équivalence entre la réponse de l'élève et la solution sol'2 | |
| resolu1 | si(qegal1,teq'2,si(kdif1,teq1|teq2,teq1)) | 1 si la réponse entrée par l'élève est une des réponses que nous acceptons comme réponse finale et 0 sinon |
| interm | 0 | Sert à interpréter les réponses intermédiaires de l'élève |
| vrai | zero(gauche(interm)-droit(interm)) | Fonction servant à établir si l'égalité de l'élève est vérifiée à 10-9 près |
Quelques compléments.
La ressource LaboMep que nous avons utilisée nous permettrait aussi de faire un exercice de calcul demandant deux valeurs finales, par exemple le calcul de AB et de AC.
Dans ce cas il nous faudrait modifier notre figure initiale qui devrait aussi contenir un calcul rep2 (pour AC), rep1 étant lui alors associé à la réponse pour AB.
Il faudrait alors créer deux autres calculs exact2 et resolu2 qui joueraient le rôle de exact1 et resolu1 de notre figure (pour la réponse de A) tandis que exact1 et resolu1 eux devraient être modifiés pour tester la réponse pour AB.
Il nous faudrait aussi alors remplacer le champ nbCalc2 par la valeur 2, le champ formulaire2, par
AB = edit1 cm et AC = edit2 cm