Table des matières
Exercice de lecture de graphique
Notre but est créer dans LaboMep un exercice analogue à cet exercice : 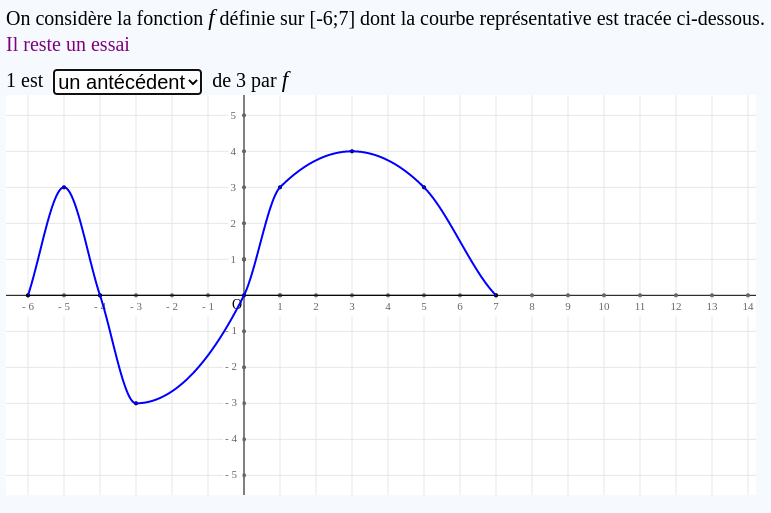
Pour créer cette ressource vous devez utiliser la version JavaScript de MathGraph32, version 6.6.0 ou ultérieure, ou utiliser la version en ligne sur le site de MathGraph32.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
Etape 1 : Création de la figure MathGraph
Commencez par créer la figure mathgraph.
Si vous désirez sauter ce qui suit vous pouvez utiliser le code Base 64 de la figure ci-dessous et, dans MathGraph32, utiliser l'icône ![]() puis choisir Figure par code Base 64.
puis choisir Figure par code Base 64.
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUeAAACygAAAQEAAAAAAAAAAQAAAMT#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAKQ1BvaW50QmFzZQD#####AAAAAAAOAAFPAMAoAAAAAAAAAAAAAAAAAAAAAAUAAEBtwAAAAAAAQGkKPXCj1wr#####AAAAAQAUQ0Ryb2l0ZURpcmVjdGlvbkZpeGUA#####wEAAAAAEAAAAQAAAAEAAAABAT#wAAAAAAAA#####wAAAAEAD0NQb2ludExpZURyb2l0ZQD#####AAAAAAEOAAFJAMAYAAAAAAAAAAAAAAAAAAAAAAUAAEBCAAAAAAAAAAAAAv####8AAAABAAlDRHJvaXRlQUIA#####wAAAAAAEAAAAQAAAAEAAAABAAAAA#####8AAAABABZDRHJvaXRlUGVycGVuZGljdWxhaXJlAP####8AAAAAABAAAAEAAAABAAAAAQAAAAT#####AAAAAQAJQ0NlcmNsZU9BAP####8BAAAAAAAAAQAAAAEAAAAD#####wAAAAEAEENJbnREcm9pdGVDZXJjbGUA#####wAAAAUAAAAG#####wAAAAEAEENQb2ludExpZUJpcG9pbnQA#####wEAAAAAEAAAAQAABQABAAAABwAAAAkA#####wAAAAABDgABSgDAKAAAAAAAAMAQAAAAAAAAAAAFAAIAAAAH#####wAAAAIAB0NSZXBlcmUA#####wDm5uYAAAABAAAAAQAAAAMAAAAJAQEAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAA#####wAAAAEACkNVbml0ZXhSZXAA#####wAEdW5pdAAAAAr#####AAAAAQALQ0hvbW90aGV0aWUA#####wAAAAH#####AAAAAQAKQ09wZXJhdGlvbgMAAAABP#AAAAAAAAD#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAAC#####8AAAABAAtDUG9pbnRJbWFnZQD#####AQAAAAAQAAJXIgEAAAEAAAAAAwAAAAz#####AAAAAQAJQ0xvbmd1ZXVyAP####8AAAABAAAADf####8AAAABAAdDQ2FsY3VsAP####8AB25iZ3JhZHgAAjIwAAAAAUA0AAAAAAAAAAAAEQD#####AAduYmdyYWR5AAIyMAAAAAFANAAAAAAAAP####8AAAABABRDSW1wbGVtZW50YXRpb25Qcm90bwD#####ABRHcmFkdWF0aW9uQXhlc1JlcGVyZQAAABsAAAAIAAAAAwAAAAoAAAAPAAAAEP####8AAAABABNDQWJzY2lzc2VPcmlnaW5lUmVwAAAAABEABWFic29yAAAACv####8AAAABABNDT3Jkb25uZWVPcmlnaW5lUmVwAAAAABEABW9yZG9yAAAACgAAAAsAAAAAEQAGdW5pdGV4AAAACv####8AAAABAApDVW5pdGV5UmVwAAAAABEABnVuaXRleQAAAAr#####AAAAAQAQQ1BvaW50RGFuc1JlcGVyZQAAAAARAAAAAAAQAAABAAAFAAAAAAoAAAAOAAAAEgAAAA4AAAATAAAAFgAAAAARAAAAAAAQAAABAAAFAAAAAAoAAAANAAAAAA4AAAASAAAADgAAABQAAAAOAAAAEwAAABYAAAAAEQAAAAAAEAAAAQAABQAAAAAKAAAADgAAABIAAAANAAAAAA4AAAATAAAADgAAABUAAAAMAAAAABEAAAAWAAAADgAAAA8AAAAPAAAAABEAAAAAABAAAAEAAAUAAAAAFwAAABkAAAAMAAAAABEAAAAWAAAADgAAABAAAAAPAAAAABEAAAAAABAAAAEAAAUAAAAAGAAAABv#####AAAAAQAIQ1NlZ21lbnQAAAAAEQEAAAAAEAAAAQAAAAEAAAAXAAAAGgAAABcAAAAAEQEAAAAAEAAAAQAAAAEAAAAYAAAAHAAAAAQAAAAAEQEAAAAACwABVwDAFAAAAAAAAMA0AAAAAAAAAAAFAAE#3FZ4mrzfDgAAAB3#####AAAAAgAIQ01lc3VyZVgAAAAAEQAGeENvb3JkAAAACgAAAB8AAAARAAAAABEABWFic3cxAAZ4Q29vcmQAAAAOAAAAIP####8AAAACABJDTGlldU9iamV0UGFyUHRMaWUBAAAAEQBmZmYAAAAAAB8AAAAOAAAADwAAAB8AAAACAAAAHwAAAB8AAAARAAAAABEABWFic3cyAA0yKmFic29yLWFic3cxAAAADQEAAAANAgAAAAFAAAAAAAAAAAAAAA4AAAASAAAADgAAACEAAAAWAAAAABEBAAAAABAAAAEAAAUAAAAACgAAAA4AAAAjAAAADgAAABMAAAAZAQAAABEAZmZmAAAAAAAkAAAADgAAAA8AAAAfAAAABQAAAB8AAAAgAAAAIQAAACMAAAAkAAAABAAAAAARAQAAAAALAAFSAEAgAAAAAAAAwCAAAAAAAAAAAAUAAT#RG06BtOgfAAAAHv####8AAAACAAhDTWVzdXJlWQAAAAARAAZ5Q29vcmQAAAAKAAAAJgAAABEAAAAAEQAFb3JkcjEABnlDb29yZAAAAA4AAAAnAAAAGQEAAAARAGZmZgAAAAAAJgAAAA4AAAAQAAAAJgAAAAIAAAAmAAAAJgAAABEAAAAAEQAFb3JkcjIADTIqb3Jkb3Itb3JkcjEAAAANAQAAAA0CAAAAAUAAAAAAAAAAAAAADgAAABMAAAAOAAAAKAAAABYAAAAAEQEAAAAAEAAAAQAABQAAAAAKAAAADgAAABIAAAAOAAAAKgAAABkBAAAAEQBmZmYAAAAAACsAAAAOAAAAEAAAACYAAAAFAAAAJgAAACcAAAAoAAAAKgAAACv#####AAAAAgAMQ0NvbW1lbnRhaXJlAAAAABEBZmZmAAAAAAAAAAAAQBgAAAAAAAAAAAAAAB8LAAH###8AAAABAAAAAAAAAAEAAAAAAAAAAAALI1ZhbChhYnN3MSkAAAAZAQAAABEAZmZmAAAAAAAtAAAADgAAAA8AAAAfAAAABAAAAB8AAAAgAAAAIQAAAC0AAAAbAAAAABEBZmZmAAAAAAAAAAAAQBgAAAAAAAAAAAAAACQLAAH###8AAAABAAAAAAAAAAEAAAAAAAAAAAALI1ZhbChhYnN3MikAAAAZAQAAABEAZmZmAAAAAAAvAAAADgAAAA8AAAAfAAAABgAAAB8AAAAgAAAAIQAAACMAAAAkAAAALwAAABsAAAAAEQFmZmYAwCAAAAAAAAA#8AAAAAAAAAAAAAAAJgsAAf###wAAAAIAAAABAAAAAQAAAAAAAAAAAAsjVmFsKG9yZHIxKQAAABkBAAAAEQBmZmYAAAAAADEAAAAOAAAAEAAAACYAAAAEAAAAJgAAACcAAAAoAAAAMQAAABsAAAAAEQFmZmYAwBwAAAAAAAAAAAAAAAAAAAAAAAAAKwsAAf###wAAAAIAAAABAAAAAQAAAAAAAAAAAAsjVmFsKG9yZHIyKQAAABkBAAAAEQBmZmYAAAAAADMAAAAOAAAAEAAAACYAAAAGAAAAJgAAACcAAAAoAAAAKgAAACsAAAAzAAAAEQD#####AAVuYnZhcgABNQAAAAFAFAAAAAAAAAAAABEA#####wAGbmJjYXMxAAEyAAAAAUAAAAAAAAAAAAAAEQD#####AAZuYmNhczIAATIAAAABQAAAAAAAAAAAAAARAP####8ABm5iY2FzMwABMgAAAAFAAAAAAAAAAAAAABEA#####wAGbmJjYXM0AAEzAAAAAUAIAAAAAAAAAAAAEQD#####AAZuYmNhczUAATcAAAABQBwAAAAAAAAAAAARAP####8AAnIxABNpbnQocmFuZCgwKSpuYmNhczEp#####wAAAAIACUNGb25jdGlvbgIAAAANAgAAABwRAAAAAQAAAAAAAAAAP+cuj18DOvgAAAAOAAAANgAAABEA#####wACcjIAE2ludChyYW5kKDApKm5iY2FzMikAAAAcAgAAAA0CAAAAHBEAAAABAAAAAAAAAAA#5Yorcvb51AAAAA4AAAA3AAAAEQD#####AAJyMwATaW50KHJhbmQoMCkqbmJjYXMzKQAAABwCAAAADQIAAAAcEQAAAAEAAAAAAAAAAD#rSmcz3YSSAAAADgAAADgAAAARAP####8AAnI0ABNpbnQocmFuZCgwKSpuYmNhczQpAAAAHAIAAAANAgAAABwRAAAAAQAAAAAAAAAAP8BJYlaQnZAAAAAOAAAAOQAAABEA#####wACcjUAE2ludChyYW5kKDApKm5iY2FzNSkAAAAcAgAAAA0CAAAAHBEAAAABAAAAAAAAAAA#tTeB3+wDAAAAAA4AAAA6AAAAEQD#####AAFrAAQyK3IxAAAADQAAAAABQAAAAAAAAAAAAAAOAAAAOwAAABEA#####wABcAAFLTMtcjIAAAANAf####8AAAABAAxDTW9pbnNVbmFpcmUAAAABQAgAAAAAAAAAAAAOAAAAPAAAABEA#####wABcQAFLTItcjMAAAANAQAAAB0AAAABQAAAAAAAAAAAAAAOAAAAPQAAABEA#####wABYQAbKHI0PTApKigtNSkrKHI0PTEpKyhyND0yKSo1AAAADQAAAAANAAAAAA0CAAAADQgAAAAOAAAAPgAAAAEAAAAAAAAAAAAAAB0AAAABQBQAAAAAAAAAAAANCAAAAA4AAAA+AAAAAT#wAAAAAAAAAAAADQIAAAANCAAAAA4AAAA+AAAAAUAAAAAAAAAAAAAAAUAUAAAAAAAAAAAAEQD#####AAFmAAQxK3I1AAAADQAAAAABP#AAAAAAAAAAAAAOAAAAPwAAABEA#####wAFZm9ybTEAA2Y9MQAAAA0IAAAADgAAAEQAAAABP#AAAAAAAAAAAAARAP####8ABWZvcm0yAANmPTIAAAANCAAAAA4AAABEAAAAAUAAAAAAAAAAAAAAEQD#####AAVmb3JtMwADZj0zAAAADQgAAAAOAAAARAAAAAFACAAAAAAAAAAAABEA#####wAFZm9ybTQAA2Y9NAAAAA0IAAAADgAAAEQAAAABQBAAAAAAAAAAAAARAP####8ABWZvcm01AANmPTUAAAANCAAAAA4AAABEAAAAAUAUAAAAAAAAAAAAEQD#####AAVmb3JtNgADZj02AAAADQgAAAAOAAAARAAAAAFAGAAAAAAAAAAAABEA#####wAFZm9ybTcAA2Y9NwAAAA0IAAAADgAAAEQAAAABQBwAAAAAAAAAAAARAP####8AAm0xAAEzAAAAAUAIAAAAAAAAAAAAEQD#####AAJtMgABMAAAAAEAAAAAAAAAAAAAABEA#####wACbTMAAi0zAAAAHQAAAAFACAAAAAAAAAAAABEA#####wACbTQAATAAAAABAAAAAAAAAAAAAAARAP####8AAm01AAEyAAAAAUAAAAAAAAAAAAAAEQD#####AAJtNgABMQAAAAE#8AAAAAAAAAAAABEA#####wACbTcAATAAAAABAAAAAAAAAAAAAAARAP####8AAm04AAItMQAAAB0AAAABP#AAAAAAAAAAAAARAP####8AAm05AAItMQAAAB0AAAABP#AAAAAAAAAAAAAWAP####8AAAAAARAAAUEAAAAAAAAAAABACAAAAAAAAAAABQAAAAAKAAAAHQAAAAFAGAAAAAAAAAAAAAEAAAAAAAAAAAAAABYA#####wAAAAABEAABQgAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAoAAAAdAAAAAUAUAAAAAAAAAAAADgAAAEAAAAAWAP####8AAAAAARAAAUMAAAAAAAAAAABACAAAAAAAAAAABQAAAAAKAAAAHQAAAAFAEAAAAAAAAAAAAAEAAAAAAAAAAAAAABYA#####wAAAAABEAABRAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAoAAAAOAAAAQgAAAA4AAABBAAAAFgD#####AAAAAAEQAAFFAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAACgAAAAE#8AAAAAAAAAAAAA4AAABAAAAAFgD#####AAAAAAEQAAFGAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAACgAAAAFACAAAAAAAAAAAAA0AAAAADgAAAEAAAAABP#AAAAAAAAAAAAAWAP####8AAAAAARAAAUcAAAAAAAAAAABACAAAAAAAAAAABQAAAAAKAAAAAUAUAAAAAAAAAAAADgAAAEAAAAAWAP####8AAAAAARAAAUgAAAAAAAAAAABACAAAAAAAAAAABQAAAAAKAAAAAUAcAAAAAAAAAAAAAQAAAAAAAAAAAAAAEQD#####AANtdDEAAm0xAAAADgAAAEwAAAARAP####8AA210MgACbTIAAAAOAAAATQAAABEA#####wADbXQzAAJtMwAAAA4AAABOAAAAEQD#####AANtdDQAAm00AAAADgAAAE8AAAARAP####8AA210NQACbTUAAAAOAAAAUAAAABEA#####wADbXQ2AAJtNgAAAA4AAABRAAAAEQD#####AANtdDcAAm03AAAADgAAAFIAAAARAP####8AA210OAACbTgAAAAOAAAAUwAAABEA#####wADbXQ5AAJtOQAAAA4AAABUAAAAEgD#####ABJDb3VyYmUgZGUgZm9uY3Rpb24AAAAwAAAAAQAAABMAAAAKAAAAXQAAAF4AAABfAAAAYAAAAGEAAABiAAAAYwAAAGQAAABlAAAAVQAAAFYAAABXAAAAWAAAAAEAAABZAAAAWgAAAFsAAABcAAAAGAAAAABmAAd4Q29vcmQxAAAACgAAAFUAAAAYAAAAAGYAB3hDb29yZDIAAAAKAAAAVgAAABgAAAAAZgAHeENvb3JkMwAAAAoAAABXAAAAGAAAAABmAAd4Q29vcmQ0AAAACgAAAFgAAAAaAAAAAGYAB3lDb29yZDEAAAAKAAAAVQAAABoAAAAAZgAHeUNvb3JkMgAAAAoAAABWAAAAGgAAAABmAAd5Q29vcmQzAAAACgAAAFcAAAAaAAAAAGYAB3lDb29yZDQAAAAKAAAAWAAAABEAAAAAZgACYTEARShtdDErbXQyKS8oeENvb3JkMi14Q29vcmQxKV4yKzIqKHlDb29yZDEteUNvb3JkMikvKHhDb29yZDIteENvb3JkMSleMwAAAA0AAAAADQMAAAANAAAAAA4AAABdAAAADgAAAF7#####AAAAAQAKQ1B1aXNzYW5jZQAAAA0BAAAADgAAAGgAAAAOAAAAZwAAAAFAAAAAAAAAAAAAAA0DAAAADQIAAAABQAAAAAAAAAAAAAANAQAAAA4AAABrAAAADgAAAGwAAAAeAAAADQEAAAAOAAAAaAAAAA4AAABnAAAAAUAIAAAAAAAAAAAAEQAAAABmAAJiMQBFKDIqbXQxK210MikvKHhDb29yZDEteENvb3JkMikrMyooeUNvb3JkMi15Q29vcmQxKS8oeENvb3JkMi14Q29vcmQxKV4yAAAADQAAAAANAwAAAA0AAAAADQIAAAABQAAAAAAAAAAAAAAOAAAAXQAAAA4AAABeAAAADQEAAAAOAAAAZwAAAA4AAABoAAAADQMAAAANAgAAAAFACAAAAAAAAAAAAA0BAAAADgAAAGwAAAAOAAAAawAAAB4AAAANAQAAAA4AAABoAAAADgAAAGcAAAABQAAAAAAAAAD#####AAAAAQAFQ0ZvbmMAAAAAZgADZjExADlhMSoodC14Q29vcmQxKV4zK2IxKih0LXhDb29yZDEpXjIrbXQxKih0LXhDb29yZDEpK3lDb29yZDEAAAANAAAAAA0AAAAADQAAAAANAgAAAA4AAABvAAAAHgAAAA0B#####wAAAAIAEUNWYXJpYWJsZUZvcm1lbGxlAAAAAAAAAA4AAABnAAAAAUAIAAAAAAAAAAAADQIAAAAOAAAAcAAAAB4AAAANAQAAACAAAAAAAAAADgAAAGcAAAABQAAAAAAAAAAAAAANAgAAAA4AAABdAAAADQEAAAAgAAAAAAAAAA4AAABnAAAADgAAAGsAAXQAAAARAAAAAGYAA2ExMQBFKG10MittdDMpLyh4Q29vcmQzLXhDb29yZDIpXjIrMiooeUNvb3JkMi15Q29vcmQzKS8oeENvb3JkMy14Q29vcmQyKV4zAAAADQAAAAANAwAAAA0AAAAADgAAAF4AAAAOAAAAXwAAAB4AAAANAQAAAA4AAABpAAAADgAAAGgAAAABQAAAAAAAAAAAAAANAwAAAA0CAAAAAUAAAAAAAAAAAAAADQEAAAAOAAAAbAAAAA4AAABtAAAAHgAAAA0BAAAADgAAAGkAAAAOAAAAaAAAAAFACAAAAAAAAAAAABEAAAAAZgADYjExAEUoMiptdDIrbXQzKS8oeENvb3JkMi14Q29vcmQzKSszKih5Q29vcmQzLXlDb29yZDIpLyh4Q29vcmQzLXhDb29yZDIpXjIAAAANAAAAAA0DAAAADQAAAAANAgAAAAFAAAAAAAAAAAAAAA4AAABeAAAADgAAAF8AAAANAQAAAA4AAABoAAAADgAAAGkAAAANAwAAAA0CAAAAAUAIAAAAAAAAAAAADQEAAAAOAAAAbQAAAA4AAABsAAAAHgAAAA0BAAAADgAAAGkAAAAOAAAAaAAAAAFAAAAAAAAAAAAAAB8AAAAAZgADZjIxADthMTEqKHQteENvb3JkMileMytiMTEqKHQteENvb3JkMileMittdDIqKHQteENvb3JkMikreUNvb3JkMgAAAA0AAAAADQAAAAANAAAAAA0CAAAADgAAAHIAAAAeAAAADQEAAAAgAAAAAAAAAA4AAABoAAAAAUAIAAAAAAAAAAAADQIAAAAOAAAAcwAAAB4AAAANAQAAACAAAAAAAAAADgAAAGgAAAABQAAAAAAAAAAAAAANAgAAAA4AAABeAAAADQEAAAAgAAAAAAAAAA4AAABoAAAADgAAAGwAAXQAAAARAAAAAGYAA2ExMgBFKG10MyttdDQpLyh4Q29vcmQ0LXhDb29yZDMpXjIrMiooeUNvb3JkMy15Q29vcmQ0KS8oeENvb3JkNC14Q29vcmQzKV4zAAAADQAAAAANAwAAAA0AAAAADgAAAF8AAAAOAAAAYAAAAB4AAAANAQAAAA4AAABqAAAADgAAAGkAAAABQAAAAAAAAAAAAAANAwAAAA0CAAAAAUAAAAAAAAAAAAAADQEAAAAOAAAAbQAAAA4AAABuAAAAHgAAAA0BAAAADgAAAGoAAAAOAAAAaQAAAAFACAAAAAAAAAAAABEAAAAAZgADYjEyAEUoMiptdDMrbXQ0KS8oeENvb3JkMy14Q29vcmQ0KSszKih5Q29vcmQ0LXlDb29yZDMpLyh4Q29vcmQ0LXhDb29yZDMpXjIAAAANAAAAAA0DAAAADQAAAAANAgAAAAFAAAAAAAAAAAAAAA4AAABfAAAADgAAAGAAAAANAQAAAA4AAABpAAAADgAAAGoAAAANAwAAAA0CAAAAAUAIAAAAAAAAAAAADQEAAAAOAAAAbgAAAA4AAABtAAAAHgAAAA0BAAAADgAAAGoAAAAOAAAAaQAAAAFAAAAAAAAAAAAAAB8AAAAAZgADZjMxADthMTIqKHQteENvb3JkMyleMytiMTIqKHQteENvb3JkMyleMittdDMqKHQteENvb3JkMykreUNvb3JkMwAAAA0AAAAADQAAAAANAAAAAA0CAAAADgAAAHUAAAAeAAAADQEAAAAgAAAAAAAAAA4AAABpAAAAAUAIAAAAAAAAAAAADQIAAAAOAAAAdgAAAB4AAAANAQAAACAAAAAAAAAADgAAAGkAAAABQAAAAAAAAAAAAAANAgAAAA4AAABfAAAADQEAAAAgAAAAAAAAAA4AAABpAAAADgAAAG0AAXQAAAAfAAAAAGYAA2YxMwBTKHQ8eENvb3JkMikqZjExKHQpKyh0Pj14Q29vcmQyKSoodDx4Q29vcmQzKSpmMjEodCkrKHQ+PXhDb29yZDMpKih0PD14Q29vcmQ0KSpmMzEodCkAAAANAAAAAA0AAAAADQIAAAANBAAAACAAAAAAAAAADgAAAGj#####AAAAAQAOQ0FwcGVsRm9uY3Rpb24AAABxAAAAIAAAAAAAAAANAgAAAA0CAAAADQcAAAAgAAAAAAAAAA4AAABoAAAADQQAAAAgAAAAAAAAAA4AAABpAAAAIQAAAHQAAAAgAAAAAAAAAA0CAAAADQIAAAANBwAAACAAAAAAAAAADgAAAGkAAAANBgAAACAAAAAAAAAADgAAAGoAAAAhAAAAdwAAACAAAAAAAAF0AAAAGAAAAABmAAd4Q29vcmQ1AAAACgAAAFgAAAAYAAAAAGYAB3hDb29yZDYAAAAKAAAAAQAAABgAAAAAZgAHeENvb3JkNwAAAAoAAABZAAAAGAAAAABmAAd4Q29vcmQ4AAAACgAAAFoAAAAaAAAAAGYAB3lDb29yZDUAAAAKAAAAWAAAABoAAAAAZgAHeUNvb3JkNgAAAAoAAAABAAAAGgAAAABmAAd5Q29vcmQ3AAAACgAAAFkAAAAaAAAAAGYAB3lDb29yZDgAAAAKAAAAWgAAABEAAAAAZgACYTEARShtdDQrbXQ1KS8oeENvb3JkNi14Q29vcmQ1KV4yKzIqKHlDb29yZDUteUNvb3JkNikvKHhDb29yZDYteENvb3JkNSleMwAAAA0AAAAADQMAAAANAAAAAA4AAABgAAAADgAAAGEAAAAeAAAADQEAAAAOAAAAegAAAA4AAAB5AAAAAUAAAAAAAAAAAAAADQMAAAANAgAAAAFAAAAAAAAAAAAAAA0BAAAADgAAAH0AAAAOAAAAfgAAAB4AAAANAQAAAA4AAAB6AAAADgAAAHkAAAABQAgAAAAAAAAAAAARAAAAAGYAAWIARSgyKm10NCttdDUpLyh4Q29vcmQ1LXhDb29yZDYpKzMqKHlDb29yZDYteUNvb3JkNSkvKHhDb29yZDYteENvb3JkNSleMgAAAA0AAAAADQMAAAANAAAAAA0CAAAAAUAAAAAAAAAAAAAADgAAAGAAAAAOAAAAYQAAAA0BAAAADgAAAHkAAAAOAAAAegAAAA0DAAAADQIAAAABQAgAAAAAAAAAAAANAQAAAA4AAAB+AAAADgAAAH0AAAAeAAAADQEAAAAOAAAAegAAAA4AAAB5AAAAAUAAAAAAAAAAAAAAHwAAAABmAANmMjIAOGExKih0LXhDb29yZDUpXjMrYioodC14Q29vcmQ1KV4yK210NCoodC14Q29vcmQ1KSt5Q29vcmQ1AAAADQAAAAANAAAAAA0AAAAADQIAAAAOAAAAgQAAAB4AAAANAQAAACAAAAAAAAAADgAAAHkAAAABQAgAAAAAAAAAAAANAgAAAA4AAACCAAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAeQAAAAFAAAAAAAAAAAAAAA0CAAAADgAAAGAAAAANAQAAACAAAAAAAAAADgAAAHkAAAAOAAAAfQABdAAAABEAAAAAZgACYTIARShtdDUrbXQ2KS8oeENvb3JkNy14Q29vcmQ2KV4yKzIqKHlDb29yZDYteUNvb3JkNykvKHhDb29yZDcteENvb3JkNileMwAAAA0AAAAADQMAAAANAAAAAA4AAABhAAAADgAAAGIAAAAeAAAADQEAAAAOAAAAewAAAA4AAAB6AAAAAUAAAAAAAAAAAAAADQMAAAANAgAAAAFAAAAAAAAAAAAAAA0BAAAADgAAAH4AAAAOAAAAfwAAAB4AAAANAQAAAA4AAAB7AAAADgAAAHoAAAABQAgAAAAAAAAAAAARAAAAAGYAAmIyAEUoMiptdDUrbXQ2KS8oeENvb3JkNi14Q29vcmQ3KSszKih5Q29vcmQ3LXlDb29yZDYpLyh4Q29vcmQ3LXhDb29yZDYpXjIAAAANAAAAAA0DAAAADQAAAAANAgAAAAFAAAAAAAAAAAAAAA4AAABhAAAADgAAAGIAAAANAQAAAA4AAAB6AAAADgAAAHsAAAANAwAAAA0CAAAAAUAIAAAAAAAAAAAADQEAAAAOAAAAfwAAAA4AAAB+AAAAHgAAAA0BAAAADgAAAHsAAAAOAAAAegAAAAFAAAAAAAAAAAAAAB8AAAAAZgADZjIzADlhMioodC14Q29vcmQ2KV4zK2IyKih0LXhDb29yZDYpXjIrbXQ1Kih0LXhDb29yZDYpK3lDb29yZDYAAAANAAAAAA0AAAAADQAAAAANAgAAAA4AAACEAAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAegAAAAFACAAAAAAAAAAAAA0CAAAADgAAAIUAAAAeAAAADQEAAAAgAAAAAAAAAA4AAAB6AAAAAUAAAAAAAAAAAAAADQIAAAAOAAAAYQAAAA0BAAAAIAAAAAAAAAAOAAAAegAAAA4AAAB+AAF0AAAAEQAAAABmAAJhMwBFKG10NittdDcpLyh4Q29vcmQ4LXhDb29yZDcpXjIrMiooeUNvb3JkNy15Q29vcmQ4KS8oeENvb3JkOC14Q29vcmQ3KV4zAAAADQAAAAANAwAAAA0AAAAADgAAAGIAAAAOAAAAYwAAAB4AAAANAQAAAA4AAAB8AAAADgAAAHsAAAABQAAAAAAAAAAAAAANAwAAAA0CAAAAAUAAAAAAAAAAAAAADQEAAAAOAAAAfwAAAA4AAACAAAAAHgAAAA0BAAAADgAAAHwAAAAOAAAAewAAAAFACAAAAAAAAAAAABEAAAAAZgACYjMARSgyKm10NittdDcpLyh4Q29vcmQ3LXhDb29yZDgpKzMqKHlDb29yZDgteUNvb3JkNykvKHhDb29yZDgteENvb3JkNyleMgAAAA0AAAAADQMAAAANAAAAAA0CAAAAAUAAAAAAAAAAAAAADgAAAGIAAAAOAAAAYwAAAA0BAAAADgAAAHsAAAAOAAAAfAAAAA0DAAAADQIAAAABQAgAAAAAAAAAAAANAQAAAA4AAACAAAAADgAAAH8AAAAeAAAADQEAAAAOAAAAfAAAAA4AAAB7AAAAAUAAAAAAAAAAAAAAHwAAAABmAANmMjQAOWEzKih0LXhDb29yZDcpXjMrYjMqKHQteENvb3JkNyleMittdDYqKHQteENvb3JkNykreUNvb3JkNwAAAA0AAAAADQAAAAANAAAAAA0CAAAADgAAAIcAAAAeAAAADQEAAAAgAAAAAAAAAA4AAAB7AAAAAUAIAAAAAAAAAAAADQIAAAAOAAAAiAAAAB4AAAANAQAAACAAAAAAAAAADgAAAHsAAAABQAAAAAAAAAAAAAANAgAAAA4AAABiAAAADQEAAAAgAAAAAAAAAA4AAAB7AAAADgAAAH8AAXQAAAAfAAAAAGYAA2YyNQBgKHQ+PXhDb29yZDUpKih0PHhDb29yZDYpKmYyMih0KSsodD49eENvb3JkNikqKHQ8eENvb3JkNykqZjIzKHQpKyh0Pj14Q29vcmQ3KSoodDw9eENvb3JkOCkqZjI0KHQpAAAADQAAAAANAAAAAA0CAAAADQIAAAANBwAAACAAAAAAAAAADgAAAHkAAAANBAAAACAAAAAAAAAADgAAAHoAAAAhAAAAgwAAACAAAAAAAAAADQIAAAANAgAAAA0HAAAAIAAAAAAAAAAOAAAAegAAAA0EAAAAIAAAAAAAAAAOAAAAewAAACEAAACGAAAAIAAAAAAAAAANAgAAAA0CAAAADQcAAAAgAAAAAAAAAA4AAAB7AAAADQYAAAAgAAAAAAAAAA4AAAB8AAAAIQAAAIkAAAAgAAAAAAABdAAAAB8AAAAAZgADZjEyADModDw9eENvb3JkNCkqZjEzKHQpKyh0PnhDb29yZDQpKih0PD14Q29vcmQ4KSpmMjUodCkAAAANAAAAAA0CAAAADQYAAAAgAAAAAAAAAA4AAABqAAAAIQAAAHgAAAAgAAAAAAAAAA0CAAAADQIAAAANBQAAACAAAAAAAAAADgAAAGoAAAANBgAAACAAAAAAAAAADgAAAHwAAAAhAAAAigAAACAAAAAAAAF0AAAAGAAAAABmAAd4Q29vcmQ5AAAACgAAAFsAAAAaAAAAAGYAB3lDb29yZDkAAAAKAAAAWwAAABEAAAAAZgACYTQARShtdDcrbXQ4KS8oeENvb3JkOS14Q29vcmQ4KV4yKzIqKHlDb29yZDgteUNvb3JkOSkvKHhDb29yZDkteENvb3JkOCleMwAAAA0AAAAADQMAAAANAAAAAA4AAABjAAAADgAAAGQAAAAeAAAADQEAAAAOAAAAjAAAAA4AAAB8AAAAAUAAAAAAAAAAAAAADQMAAAANAgAAAAFAAAAAAAAAAAAAAA0BAAAADgAAAIAAAAAOAAAAjQAAAB4AAAANAQAAAA4AAACMAAAADgAAAHwAAAABQAgAAAAAAAAAAAARAAAAAGYAAmI0AEUoMiptdDcrbXQ4KS8oeENvb3JkOC14Q29vcmQ5KSszKih5Q29vcmQ5LXlDb29yZDgpLyh4Q29vcmQ5LXhDb29yZDgpXjIAAAANAAAAAA0DAAAADQAAAAANAgAAAAFAAAAAAAAAAAAAAA4AAABjAAAADgAAAGQAAAANAQAAAA4AAAB8AAAADgAAAIwAAAANAwAAAA0CAAAAAUAIAAAAAAAAAAAADQEAAAAOAAAAjQAAAA4AAACAAAAAHgAAAA0BAAAADgAAAIwAAAAOAAAAfAAAAAFAAAAAAAAAAAAAAB8AAAAAZgADZjI2ADlhNCoodC14Q29vcmQ4KV4zK2I0Kih0LXhDb29yZDgpXjIrbXQ3Kih0LXhDb29yZDgpK3lDb29yZDgAAAANAAAAAA0AAAAADQAAAAANAgAAAA4AAACOAAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAfAAAAAFACAAAAAAAAAAAAA0CAAAADgAAAI8AAAAeAAAADQEAAAAgAAAAAAAAAA4AAAB8AAAAAUAAAAAAAAAAAAAADQIAAAAOAAAAYwAAAA0BAAAAIAAAAAAAAAAOAAAAfAAAAA4AAACAAAF0AAAAHwAAAABmAAJmMQAmKHQ8PXhDb29yZDgpKmYxMih0KSsodD54Q29vcmQ4KSpmMjYodCkAAAANAAAAAA0CAAAADQYAAAAgAAAAAAAAAA4AAAB8AAAAIQAAAIsAAAAgAAAAAAAAAA0CAAAADQUAAAAgAAAAAAAAAA4AAAB8AAAAIQAAAJAAAAAgAAAAAAABdAAAABgAAAAAZgAIeENvb3JkMTAAAAAKAAAAXAAAABoAAAAAZgAIeUNvb3JkMTAAAAAKAAAAXAAAABEAAAAAZgACYTUASChtdDgrbXQ5KS8oeENvb3JkMTAteENvb3JkOSleMisyKih5Q29vcmQ5LXlDb29yZDEwKS8oeENvb3JkMTAteENvb3JkOSleMwAAAA0AAAAADQMAAAANAAAAAA4AAABkAAAADgAAAGUAAAAeAAAADQEAAAAOAAAAkgAAAA4AAACMAAAAAUAAAAAAAAAAAAAADQMAAAANAgAAAAFAAAAAAAAAAAAAAA0BAAAADgAAAI0AAAAOAAAAkwAAAB4AAAANAQAAAA4AAACSAAAADgAAAIwAAAABQAgAAAAAAAAAAAARAAAAAGYAAmI1AEgoMiptdDgrbXQ5KS8oeENvb3JkOS14Q29vcmQxMCkrMyooeUNvb3JkMTAteUNvb3JkOSkvKHhDb29yZDEwLXhDb29yZDkpXjIAAAANAAAAAA0DAAAADQAAAAANAgAAAAFAAAAAAAAAAAAAAA4AAABkAAAADgAAAGUAAAANAQAAAA4AAACMAAAADgAAAJIAAAANAwAAAA0CAAAAAUAIAAAAAAAAAAAADQEAAAAOAAAAkwAAAA4AAACNAAAAHgAAAA0BAAAADgAAAJIAAAAOAAAAjAAAAAFAAAAAAAAAAAAAAB8AAAAAZgACZjIAOWE1Kih0LXhDb29yZDkpXjMrYjUqKHQteENvb3JkOSleMittdDgqKHQteENvb3JkOSkreUNvb3JkOQAAAA0AAAAADQAAAAANAAAAAA0CAAAADgAAAJQAAAAeAAAADQEAAAAgAAAAAAAAAA4AAACMAAAAAUAIAAAAAAAAAAAADQIAAAAOAAAAlQAAAB4AAAANAQAAACAAAAAAAAAADgAAAIwAAAABQAAAAAAAAAAAAAANAgAAAA4AAABkAAAADQEAAAAgAAAAAAAAAA4AAACMAAAADgAAAI0AAXQAAAAfAQAAAGYAAWcAJCh0PD14Q29vcmQ5KSpmMSh0KSsodD54Q29vcmQ5KSpmMih0KQAAAA0AAAAADQIAAAANBgAAACAAAAAAAAAADgAAAIwAAAAhAAAAkQAAACAAAAAAAAAADQIAAAANBQAAACAAAAAAAAAADgAAAIwAAAAhAAAAlgAAACAAAAAAAAF0AAAAFwD#####AAAAAAAQAAABAAAAAQAAAFUAAABcAAAABAD#####AQAAAAAQAAJ4MQAAAAAAAAAAAEAIAAAAAAAAAAAFAAEAAAAAAAAAAAAAAJgAAAAYAP####8AAngxAAAACgAAAJkAAAARAP####8AAnkxAAVnKHgxKQAAACEAAACXAAAADgAAAJoAAAAWAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAoAAAAOAAAAmgAAAA4AAACb#####wAAAAIADUNMaWV1RGVQb2ludHMA#####wAAAP8AAAACAAAAnAAAAfQAAQAAAJkAAAAEAAAAmQAAAJoAAACbAAAAnP####8AAAACAAZDTGF0ZXgA#####wEAAAABAAZlbm9uY2X#####EEB#cAAAAAAAQFQ1wo9cKPYAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAOpcYmVnaW57YXJyYXl9e2x9Clx0ZXh0e09uIGNvbnNpZMOocmUgbGEgZm9uY3Rpb24gJGYkIGTDqWZpbmllIHN1ciBbLTY7N10gZG9udCBsYSBjb3VyYmUgcmVwcsOpc2VudGF0aXZlIGVzdCB0cmFjw6llIGNpLWRlc3NvdXMuIAp9ClxcIFx0ZXh0e0NsaXF1ZXIgc3VyIGxlIGJvdXRvbiBPSyBvdSB0YXBlciBzdXIgbGEgdG91Y2hlIEVudHLDqWUgcG91ciB2YWxpZGVyIGxhIHLDqXBvbnNlLn0KXGVuZHthcnJheX0AAAAjAP####8BAAAAAQAKZm9ybXVsYWlyZf####8QQITAAAAAAABAbso9cKPXCgAAAAAAAAAAAAAAAAABAAAAAAAAAAAB7lxJZntmb3JtMX0KewpcdGV4dHtcVmFse2F9IGVzdCBsaXN0MSBkZSBcVmFse2t9IHBhciAkZiR9Cn0KewpcSWZ7Zm9ybTJ9CnsKXHRleHR7VW4gYW50w6ljw6lkZW50IGRlIDAgcGFyICRmJCBlc3QgZWRpdDF9Cn0KewpcSWZ7Zm9ybTN9CnsKXHRleHR7XFZhbHtrfSBlc3QgbGlzdDEgZGUgXFZhbHthfSBwYXIgJGYkfQp9CnsKXElme2Zvcm00fQp7Clx0ZXh0e1xWYWx7a30gYWRtZXQgZWRpdDEgYW50w6ljw6lkZW50cyBwYXIgJGYkfQp9CnsKXElme2Zvcm01fQp7Clx0ZXh0e1VuIG5vbWJyZSBheWFudCBleGFjdGVtZW50IDQgYW50w6ljw6lkZW50cyBwYXIgJGYkIGVzdCBlZGl0MX0KfQp7ClxJZntmb3JtNn0KewpcdGV4dHtVbiBub21icmUgYXlhbnQgZXhhY3RlbWVudCAyIGFudMOpY8OpZGVudHMgcGFyICRmJCBlc3QgZWRpdDF9Cn0KewpcdGV4dHtVbiBub21icmUgYXlhbnQgdW4gc2V1bCBhbnTDqWPDqWRlbnQgcGFyICRmJCBlc3QgZWRpdDF9Cn0KfQp9Cn0KfQp9AAAAEQD#####AARyZXAxAAEwAAAAAQAAAAAAAAAAAAAAEQD#####AAZleGFjdDEAlXNpKGZvcm0yLHJlcDE9LTZ8cmVwMT0tNHxyZXAxPTB8cmVwMT03LHNpKGZvcm00LHJlcDE9MyxzaShmb3JtNSxyZXAxPGsmcmVwMT49MCxzaShmb3JtNixyZXAxPDAmcmVwMT5wfHJlcDE+ayZyZXAxPGsrMSxzaShmb3JtNyxyZXAxPXB8cmVwMT1rKzEsMCkpKSkp#####wAAAAEADUNGb25jdGlvbjNWYXIAAAAADgAAAEYAAAANCwAAAA0LAAAADQsAAAANCAAAAA4AAACgAAAAHQAAAAFAGAAAAAAAAAAAAA0IAAAADgAAAKAAAAAdAAAAAUAQAAAAAAAAAAAADQgAAAAOAAAAoAAAAAEAAAAAAAAAAAAAAA0IAAAADgAAAKAAAAABQBwAAAAAAAAAAAAkAAAAAA4AAABIAAAADQgAAAAOAAAAoAAAAAFACAAAAAAAAAAAACQAAAAADgAAAEkAAAANCgAAAA0EAAAADgAAAKAAAAAOAAAAQAAAAA0HAAAADgAAAKAAAAABAAAAAAAAAAAAAAAkAAAAAA4AAABKAAAADQsAAAANCgAAAA0EAAAADgAAAKAAAAABAAAAAAAAAAAAAAANBQAAAA4AAACgAAAADgAAAEEAAAANCgAAAA0FAAAADgAAAKAAAAAOAAAAQAAAAA0EAAAADgAAAKAAAAANAAAAAA4AAABAAAAAAT#wAAAAAAAAAAAAJAAAAAAOAAAASwAAAA0LAAAADQgAAAAOAAAAoAAAAA4AAABBAAAADQgAAAAOAAAAoAAAAA0AAAAADgAAAEAAAAABP#AAAAAAAAAAAAABAAAAAAAAAAAAAAARAP####8AB3Jlc29sdTEABmV4YWN0MQAAAA4AAAChAAAAEQD#####AAhyZXNsaXN0MQATc2koZm9ybTF8Zm9ybTMsMSwwKQAAACQAAAAADQsAAAAOAAAARQAAAA4AAABHAAAAAT#wAAAAAAAAAAAAAQAAAAAAAAAAAAAAIwD#####AQAAAAEABWxpc3Qx#####xBAhOAAAAAAAEBxNR64UeuFAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAC1XElme2Zvcm0xfQp7ClxiZWdpbnthcnJheX17bH0KXHRleHR7dW4gYW50w6ljw6lkZW50IH0gClxcIFx0ZXh0e2wnaW1hZ2UgfQpcZW5ke2FycmF5fQp9CnsKXElme2Zvcm0zfQp7ClxiZWdpbnthcnJheX17bH0KXHRleHR7bCdpbWFnZX0gClxcIFx0ZXh0e1VuIGFudMOpY8OpZGVudH0KXGVuZHthcnJheX0KfQp7Cn0KfQAAAAQA#####wF#AAABEAABSwAAAAAAAAAAAEAIAAAAAAAAAAABAAG#9xxxxxxxywAAAAX#####AAAAAQAQQ0Ryb2l0ZVBhcmFsbGVsZQD#####AX8AAAAQAAABAAAAAQAAAKUAAAAEAAAAGgD#####AAFtAAAACgAAAKUAAAAfAP####8ABHplcm8ADGFicyh4KTw9MC4wMQAAAA0GAAAAHAAAAAAgAAAAAAAAAAE#hHrhR64UewABeAAAABEA#####wACbScANXNpKHplcm8obS1rKSxrLHNpKHplcm8obS1wKSxwLHNpKHplcm8obS1rLTEpLGsrMSxtKSkpAAAAJAAAAAAhAAAAqAAAAA0BAAAADgAAAKcAAAAOAAAAQAAAAA4AAABAAAAAJAAAAAAhAAAAqAAAAA0BAAAADgAAAKcAAAAOAAAAQQAAAA4AAABBAAAAJAAAAAAhAAAAqAAAAA0BAAAADQEAAAAOAAAApwAAAA4AAABAAAAAAT#wAAAAAAAAAAAADQAAAAAOAAAAQAAAAAE#8AAAAAAAAAAAAA4AAACn#####wAAAAIAEUNTb2x1dGlvbkVxdWF0aW9uAP####8AAnMxAAF4AAAADQgAAAAhAAAAlwAAACAAAAAAAAAADgAAAKkAAAANAQAAACEAAACXAAAAIAAAAAAAAAAOAAAAqQAAAB0AAAABQBgAAAAAAAAAAAAdAAAAAUAUAAAAAAAAAAAAAT561#KavK9IAAAAJgD#####AAJzMgABeAAAAA0IAAAAIQAAAJcAAAAgAAAAAAAAAA4AAACpAAAADQEAAAAhAAAAlwAAACAAAAAAAAAADgAAAKkAAAAdAAAAAUAT#+XJHRTkAAAADgAAAEIAAAABPnrX8pq8r0gAAAAmAP####8AAnMzAAF4AAAADQgAAAAhAAAAlwAAACAAAAAAAAAADgAAAKkAAAANAQAAACEAAACXAAAAIAAAAAAAAAAOAAAAqQAAAA0AAAAADgAAAEIAAAABPxo24uscQy0AAAABQAgAAAAAAAAAAAABPnrX8pq8r0gAAAAmAP####8AAnM0AAF4AAAADQgAAAAhAAAAlwAAACAAAAAAAAAADgAAAKkAAAANAQAAACEAAACXAAAAIAAAAAAAAAAOAAAAqQAAAAFACAA0bcXWOQAAAAFAHAAAAAAAAAAAAAE+etfymryvSAAAABYA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAACgAAAA4AAACqAAAADgAAAKcAAAAWAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAoAAAAOAAAAqwAAAA4AAACnAAAAFgD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAKAAAADgAAAKwAAAAOAAAApwAAABYA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAACgAAAA4AAACtAAAADgAAAKcAAAAWAP####8B#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAABAAAAAAoAAAAOAAAAqgAAAAEAAAAAAAAAAAAAABYA#####wH#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAEAAAAACgAAAA4AAACrAAAAAQAAAAAAAAAAAAAAFgD#####Af8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAAAQAAAAAKAAAADgAAAKwAAAABAAAAAAAAAAAAAAAWAP####8B#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAABAAAAAAoAAAAOAAAArQAAAAEAAAAAAAAAAAAAABcA#####wEAAAAAEAAAAQAAAQEAAACuAAAAsgAAABcA#####wEAAAAAEAAAAQAAAQEAAACvAAAAswAAABcA#####wEAAAAAEAAAAQAAAQEAAACwAAAAtAAAABcA#####wEAAAAAEAAAAQAAAQEAAACxAAAAtf####8AAAABAA9DVmFsZXVyQWZmaWNoZWUA#####wF#AAAAwCIAAAAAAADACAAAAAAAAAAAAAAApRAAAf###wAAAAIAAAACAAAAAQAAAAAAAAAAAAgjSW0jTiA9IAAAAgAAAKn#####AAAAAQAOQ1Rlc3RFeGlzdGVuY2UA#####wACdDEAAACqAAAAKAD#####AAJ0MgAAAKsAAAAoAP####8AAnQzAAAArAAAACgA#####wACdDQAAACtAAAAEQD#####AANuYnMAC3QxK3QyK3QzK3Q0AAAADQAAAAANAAAAAA0AAAAADgAAALsAAAAOAAAAvAAAAA4AAAC9AAAADgAAAL4AAAAjAP####8BfwAAAQAA#####xBAddAAAAAAAEBztR64UeuFAAH###8AAAAAAAAAAAAAAAEAAAAAAAAAAACwXGJlZ2lue2FycmF5fXtsfQpcdGV4dHtMJ8OpcXVhdGlvbiB9Zih4KT1cVmFse20nLDJ9IFx0ZXh0eyBhZG1ldCB9XFZhbHtuYnN9XHRleHR7IHNvbHV0aW9uKHMpfSAKXFwgXFZhbHttJywyfSBcdGV4dHsgYWRtZXQgfVxWYWx7bmJzfSBcdGV4dHsgYW50w6ljw6lkZW50KHMpIHBhciB9Zi4KXGVuZHthcnJheX0AAAAbAP####8BAAD#AQAA#####xBACAAAAAAAAEB2JR64UeuFAQHv7#sAAAAAAAAAAAAAAAEAAAAAAAAAAAAvT24gcGV1dCBjYXB0dXJlciAjSW0jTiBzdXIgbCdheGUgZGVzIG9yZG9ubsOpZXP#####AAAAAQAQQ01hY3JvQXBwYXJpdGlvbgD#####AQAA#wEAAP####8QQH4AAAAAAABANVHrhR64UgIB####AAAAAAAAAAAAAAABAAAAAAAAAAAACHNvbHV0aW9uAAAAAAARAAAApQAAAKYAAAC6AAAArgAAAK8AAACwAAAAsQAAALIAAACzAAAAtAAAALUAAAC2AAAAtwAAALgAAAC5AAAAwAAAAMEA#####wAAAAEAEUNNYWNyb0Rpc3Bhcml0aW9uAP####8BAAD#AQAA#####xBAffAAAAAAAEBJKPXCj1wpAgH###8AAAAAAAAAAAAAAAEAAAAAAAAAAAAQbWFzcXVlciBzb2x1dGlvbgAAAAAAEQAAAKUAAACmAAAAugAAAK4AAACvAAAAsAAAALEAAACyAAAAswAAALQAAAC1AAAAtgAAALcAAAC4AAAAuQAAAMAAAADBAAAADv##########
Sinon :
Pour que notre tutoriel ne soit pas trop long nous allons sauter certaines étapes de la création de la figure.
L'idée est de poser des questions sur une fonction définie sur l'intervalle [-6;7] en apportant de façon aléatoire certaines petites modifications à la courbe lors des répétitions successives.
Utiliser l'icône ![]() puis choisissez Figure par code Base 64.
puis choisissez Figure par code Base 64.
Collez le code Base 64 contenu ci-dessous :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAP5AAAChwAAAQEAAAAAAAAAAQAAAJf#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAKQ1BvaW50QmFzZQD#####AAAAAAAOAAFPAMAoAAAAAAAAAAAAAAAAAAAAAAUAAEBtwAAAAAAAQGkKPXCj1wr#####AAAAAQAUQ0Ryb2l0ZURpcmVjdGlvbkZpeGUA#####wEAAAAAEAAAAQAAAAEAAAABAT#wAAAAAAAA#####wAAAAEAD0NQb2ludExpZURyb2l0ZQD#####AAAAAAEOAAFJAMAYAAAAAAAAAAAAAAAAAAAAAAUAAEBCAAAAAAAAAAAAAv####8AAAABAAlDRHJvaXRlQUIA#####wAAAAAAEAAAAQAAAAEAAAABAAAAA#####8AAAABABZDRHJvaXRlUGVycGVuZGljdWxhaXJlAP####8AAAAAABAAAAEAAAABAAAAAQAAAAT#####AAAAAQAJQ0NlcmNsZU9BAP####8BAAAAAAAAAQAAAAEAAAAD#####wAAAAEAEENJbnREcm9pdGVDZXJjbGUA#####wAAAAUAAAAG#####wAAAAEAEENQb2ludExpZUJpcG9pbnQA#####wEAAAAAEAAAAQAABQABAAAABwAAAAkA#####wAAAAABDgABSgDAKAAAAAAAAMAQAAAAAAAAAAAFAAIAAAAH#####wAAAAIAB0NSZXBlcmUA#####wDm5uYAAAABAAAAAQAAAAMAAAAJAQEAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAA#####wAAAAEACkNVbml0ZXhSZXAA#####wAEdW5pdAAAAAr#####AAAAAQALQ0hvbW90aGV0aWUA#####wAAAAH#####AAAAAQAKQ09wZXJhdGlvbgMAAAABP#AAAAAAAAD#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAAC#####8AAAABAAtDUG9pbnRJbWFnZQD#####AQAAAAAQAAJXIgEAAAEAAAAAAwAAAAz#####AAAAAQAJQ0xvbmd1ZXVyAP####8AAAABAAAADf####8AAAABAAdDQ2FsY3VsAP####8AB25iZ3JhZHgAAjIwAAAAAUA0AAAAAAAAAAAAEQD#####AAduYmdyYWR5AAIyMAAAAAFANAAAAAAAAP####8AAAABABRDSW1wbGVtZW50YXRpb25Qcm90bwD#####ABRHcmFkdWF0aW9uQXhlc1JlcGVyZQAAABsAAAAIAAAAAwAAAAoAAAAPAAAAEP####8AAAABABNDQWJzY2lzc2VPcmlnaW5lUmVwAAAAABEABWFic29yAAAACv####8AAAABABNDT3Jkb25uZWVPcmlnaW5lUmVwAAAAABEABW9yZG9yAAAACgAAAAsAAAAAEQAGdW5pdGV4AAAACv####8AAAABAApDVW5pdGV5UmVwAAAAABEABnVuaXRleQAAAAr#####AAAAAQAQQ1BvaW50RGFuc1JlcGVyZQAAAAARAAAAAAAQAAABAAAFAAAAAAoAAAAOAAAAEgAAAA4AAAATAAAAFgAAAAARAAAAAAAQAAABAAAFAAAAAAoAAAANAAAAAA4AAAASAAAADgAAABQAAAAOAAAAEwAAABYAAAAAEQAAAAAAEAAAAQAABQAAAAAKAAAADgAAABIAAAANAAAAAA4AAAATAAAADgAAABUAAAAMAAAAABEAAAAWAAAADgAAAA8AAAAPAAAAABEAAAAAABAAAAEAAAUAAAAAFwAAABkAAAAMAAAAABEAAAAWAAAADgAAABAAAAAPAAAAABEAAAAAABAAAAEAAAUAAAAAGAAAABv#####AAAAAQAIQ1NlZ21lbnQAAAAAEQEAAAAAEAAAAQAAAAEAAAAXAAAAGgAAABcAAAAAEQEAAAAAEAAAAQAAAAEAAAAYAAAAHAAAAAQAAAAAEQEAAAAACwABVwDAFAAAAAAAAMA0AAAAAAAAAAAFAAE#3FZ4mrzfDgAAAB3#####AAAAAgAIQ01lc3VyZVgAAAAAEQAGeENvb3JkAAAACgAAAB8AAAARAAAAABEABWFic3cxAAZ4Q29vcmQAAAAOAAAAIP####8AAAACABJDTGlldU9iamV0UGFyUHRMaWUBAAAAEQBmZmYAAAAAAB8AAAAOAAAADwAAAB8AAAACAAAAHwAAAB8AAAARAAAAABEABWFic3cyAA0yKmFic29yLWFic3cxAAAADQEAAAANAgAAAAFAAAAAAAAAAAAAAA4AAAASAAAADgAAACEAAAAWAAAAABEBAAAAABAAAAEAAAUAAAAACgAAAA4AAAAjAAAADgAAABMAAAAZAQAAABEAZmZmAAAAAAAkAAAADgAAAA8AAAAfAAAABQAAAB8AAAAgAAAAIQAAACMAAAAkAAAABAAAAAARAQAAAAALAAFSAEAgAAAAAAAAwCAAAAAAAAAAAAUAAT#RG06BtOgfAAAAHv####8AAAACAAhDTWVzdXJlWQAAAAARAAZ5Q29vcmQAAAAKAAAAJgAAABEAAAAAEQAFb3JkcjEABnlDb29yZAAAAA4AAAAnAAAAGQEAAAARAGZmZgAAAAAAJgAAAA4AAAAQAAAAJgAAAAIAAAAmAAAAJgAAABEAAAAAEQAFb3JkcjIADTIqb3Jkb3Itb3JkcjEAAAANAQAAAA0CAAAAAUAAAAAAAAAAAAAADgAAABMAAAAOAAAAKAAAABYAAAAAEQEAAAAAEAAAAQAABQAAAAAKAAAADgAAABIAAAAOAAAAKgAAABkBAAAAEQBmZmYAAAAAACsAAAAOAAAAEAAAACYAAAAFAAAAJgAAACcAAAAoAAAAKgAAACv#####AAAAAgAMQ0NvbW1lbnRhaXJlAAAAABEBZmZmAAAAAAAAAAAAQBgAAAAAAAAAAAAAAB8LAAH###8AAAABAAAAAAAAAAEAAAAAAAAAAAALI1ZhbChhYnN3MSkAAAAZAQAAABEAZmZmAAAAAAAtAAAADgAAAA8AAAAfAAAABAAAAB8AAAAgAAAAIQAAAC0AAAAbAAAAABEBZmZmAAAAAAAAAAAAQBgAAAAAAAAAAAAAACQLAAH###8AAAABAAAAAAAAAAEAAAAAAAAAAAALI1ZhbChhYnN3MikAAAAZAQAAABEAZmZmAAAAAAAvAAAADgAAAA8AAAAfAAAABgAAAB8AAAAgAAAAIQAAACMAAAAkAAAALwAAABsAAAAAEQFmZmYAwCAAAAAAAAA#8AAAAAAAAAAAAAAAJgsAAf###wAAAAIAAAABAAAAAQAAAAAAAAAAAAsjVmFsKG9yZHIxKQAAABkBAAAAEQBmZmYAAAAAADEAAAAOAAAAEAAAACYAAAAEAAAAJgAAACcAAAAoAAAAMQAAABsAAAAAEQFmZmYAwBwAAAAAAAAAAAAAAAAAAAAAAAAAKwsAAf###wAAAAIAAAABAAAAAQAAAAAAAAAAAAsjVmFsKG9yZHIyKQAAABkBAAAAEQBmZmYAAAAAADMAAAAOAAAAEAAAACYAAAAGAAAAJgAAACcAAAAoAAAAKgAAACsAAAAzAAAAEQD#####AAVuYnZhcgABNQAAAAFAFAAAAAAAAAAAABEA#####wAGbmJjYXMxAAEyAAAAAUAAAAAAAAAAAAAAEQD#####AAZuYmNhczIAATIAAAABQAAAAAAAAAAAAAARAP####8ABm5iY2FzMwABMgAAAAFAAAAAAAAAAAAAABEA#####wAGbmJjYXM0AAEzAAAAAUAIAAAAAAAAAAAAEQD#####AAZuYmNhczUAATcAAAABQBwAAAAAAAAAAAARAP####8AAnIxABNpbnQocmFuZCgwKSpuYmNhczEp#####wAAAAIACUNGb25jdGlvbgIAAAANAgAAABwRAAAAAQAAAAAAAAAAP+cuj18DOvgAAAAOAAAANgAAABEA#####wACcjIAE2ludChyYW5kKDApKm5iY2FzMikAAAAcAgAAAA0CAAAAHBEAAAABAAAAAAAAAAA#5Yorcvb51AAAAA4AAAA3AAAAEQD#####AAJyMwATaW50KHJhbmQoMCkqbmJjYXMzKQAAABwCAAAADQIAAAAcEQAAAAEAAAAAAAAAAD#rSmcz3YSSAAAADgAAADgAAAARAP####8AAnI0ABNpbnQocmFuZCgwKSpuYmNhczQpAAAAHAIAAAANAgAAABwRAAAAAQAAAAAAAAAAP8BJYlaQnZAAAAAOAAAAOQAAABEA#####wACcjUAE2ludChyYW5kKDApKm5iY2FzNSkAAAAcAgAAAA0CAAAAHBEAAAABAAAAAAAAAAA#tTeB3+wDAAAAAA4AAAA6AAAAEQD#####AAFrAAQyK3IxAAAADQAAAAABQAAAAAAAAAAAAAAOAAAAOwAAABEA#####wABcAAFLTMtcjIAAAANAf####8AAAABAAxDTW9pbnNVbmFpcmUAAAABQAgAAAAAAAAAAAAOAAAAPAAAABEA#####wABcQAFLTItcjMAAAANAQAAAB0AAAABQAAAAAAAAAAAAAAOAAAAPQAAABEA#####wABYQAbKHI0PTApKigtNSkrKHI0PTEpKyhyND0yKSo1AAAADQAAAAANAAAAAA0CAAAADQgAAAAOAAAAPgAAAAEAAAAAAAAAAAAAAB0AAAABQBQAAAAAAAAAAAANCAAAAA4AAAA+AAAAAT#wAAAAAAAAAAAADQIAAAANCAAAAA4AAAA+AAAAAUAAAAAAAAAAAAAAAUAUAAAAAAAAAAAAEQD#####AAFmAAQxK3I1AAAADQAAAAABP#AAAAAAAAAAAAAOAAAAPwAAABEA#####wACbTEAATMAAAABQAgAAAAAAAAAAAARAP####8AAm0yAAEwAAAAAQAAAAAAAAAAAAAAEQD#####AAJtMwACLTMAAAAdAAAAAUAIAAAAAAAAAAAAEQD#####AAJtNAABMAAAAAEAAAAAAAAAAAAAABEA#####wACbTUAATIAAAABQAAAAAAAAAAAAAARAP####8AAm02AAExAAAAAT#wAAAAAAAAAAAAEQD#####AAJtNwABMAAAAAEAAAAAAAAAAAAAABEA#####wACbTgAAi0xAAAAHQAAAAE#8AAAAAAAAAAAABEA#####wACbTkAAi0xAAAAHQAAAAE#8AAAAAAAAAAAABYA#####wAAAAABEAABQQAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAoAAAAdAAAAAUAYAAAAAAAAAAAAAQAAAAAAAAAAAAAAFgD#####AAAAAAEQAAFCAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAACgAAAB0AAAABQBQAAAAAAAAAAAAOAAAAQAAAABYA#####wAAAAABEAABQwAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAoAAAAdAAAAAUAQAAAAAAAAAAAAAQAAAAAAAAAAAAAAFgD#####AAAAAAEQAAFEAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAACgAAAA4AAABCAAAADgAAAEEAAAAWAP####8AAAAAARAAAUUAAAAAAAAAAABACAAAAAAAAAAABQAAAAAKAAAAAT#wAAAAAAAAAAAADgAAAEAAAAAWAP####8AAAAAARAAAUYAAAAAAAAAAABACAAAAAAAAAAABQAAAAAKAAAAAUAIAAAAAAAAAAAADQAAAAAOAAAAQAAAAAE#8AAAAAAAAAAAABYA#####wAAAAABEAABRwAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAoAAAABQBQAAAAAAAAAAAAOAAAAQAAAABYA#####wAAAAABEAABSAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAAoAAAABQBwAAAAAAAAAAAABAAAAAAAAAAAAAAARAP####8AA210MQACbTEAAAAOAAAARQAAABEA#####wADbXQyAAJtMgAAAA4AAABGAAAAEQD#####AANtdDMAAm0zAAAADgAAAEcAAAARAP####8AA210NAACbTQAAAAOAAAASAAAABEA#####wADbXQ1AAJtNQAAAA4AAABJAAAAEQD#####AANtdDYAAm02AAAADgAAAEoAAAARAP####8AA210NwACbTcAAAAOAAAASwAAABEA#####wADbXQ4AAJtOAAAAA4AAABMAAAAEQD#####AANtdDkAAm05AAAADgAAAE0AAAASAP####8AEkNvdXJiZSBkZSBmb25jdGlvbgAAADAAAAABAAAAEwAAAAoAAABWAAAAVwAAAFgAAABZAAAAWgAAAFsAAABcAAAAXQAAAF4AAABOAAAATwAAAFAAAABRAAAAAQAAAFIAAABTAAAAVAAAAFUAAAAYAAAAAF8AB3hDb29yZDEAAAAKAAAATgAAABgAAAAAXwAHeENvb3JkMgAAAAoAAABPAAAAGAAAAABfAAd4Q29vcmQzAAAACgAAAFAAAAAYAAAAAF8AB3hDb29yZDQAAAAKAAAAUQAAABoAAAAAXwAHeUNvb3JkMQAAAAoAAABOAAAAGgAAAABfAAd5Q29vcmQyAAAACgAAAE8AAAAaAAAAAF8AB3lDb29yZDMAAAAKAAAAUAAAABoAAAAAXwAHeUNvb3JkNAAAAAoAAABRAAAAEQAAAABfAAJhMQBFKG10MSttdDIpLyh4Q29vcmQyLXhDb29yZDEpXjIrMiooeUNvb3JkMS15Q29vcmQyKS8oeENvb3JkMi14Q29vcmQxKV4zAAAADQAAAAANAwAAAA0AAAAADgAAAFYAAAAOAAAAV#####8AAAABAApDUHVpc3NhbmNlAAAADQEAAAAOAAAAYQAAAA4AAABgAAAAAUAAAAAAAAAAAAAADQMAAAANAgAAAAFAAAAAAAAAAAAAAA0BAAAADgAAAGQAAAAOAAAAZQAAAB4AAAANAQAAAA4AAABhAAAADgAAAGAAAAABQAgAAAAAAAAAAAARAAAAAF8AAmIxAEUoMiptdDErbXQyKS8oeENvb3JkMS14Q29vcmQyKSszKih5Q29vcmQyLXlDb29yZDEpLyh4Q29vcmQyLXhDb29yZDEpXjIAAAANAAAAAA0DAAAADQAAAAANAgAAAAFAAAAAAAAAAAAAAA4AAABWAAAADgAAAFcAAAANAQAAAA4AAABgAAAADgAAAGEAAAANAwAAAA0CAAAAAUAIAAAAAAAAAAAADQEAAAAOAAAAZQAAAA4AAABkAAAAHgAAAA0BAAAADgAAAGEAAAAOAAAAYAAAAAFAAAAAAAAAAP####8AAAABAAVDRm9uYwAAAABfAANmMTEAOWExKih0LXhDb29yZDEpXjMrYjEqKHQteENvb3JkMSleMittdDEqKHQteENvb3JkMSkreUNvb3JkMQAAAA0AAAAADQAAAAANAAAAAA0CAAAADgAAAGgAAAAeAAAADQH#####AAAAAgARQ1ZhcmlhYmxlRm9ybWVsbGUAAAAAAAAADgAAAGAAAAABQAgAAAAAAAAAAAANAgAAAA4AAABpAAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAYAAAAAFAAAAAAAAAAAAAAA0CAAAADgAAAFYAAAANAQAAACAAAAAAAAAADgAAAGAAAAAOAAAAZAABdAAAABEAAAAAXwADYTExAEUobXQyK210MykvKHhDb29yZDMteENvb3JkMileMisyKih5Q29vcmQyLXlDb29yZDMpLyh4Q29vcmQzLXhDb29yZDIpXjMAAAANAAAAAA0DAAAADQAAAAAOAAAAVwAAAA4AAABYAAAAHgAAAA0BAAAADgAAAGIAAAAOAAAAYQAAAAFAAAAAAAAAAAAAAA0DAAAADQIAAAABQAAAAAAAAAAAAAANAQAAAA4AAABlAAAADgAAAGYAAAAeAAAADQEAAAAOAAAAYgAAAA4AAABhAAAAAUAIAAAAAAAAAAAAEQAAAABfAANiMTEARSgyKm10MittdDMpLyh4Q29vcmQyLXhDb29yZDMpKzMqKHlDb29yZDMteUNvb3JkMikvKHhDb29yZDMteENvb3JkMileMgAAAA0AAAAADQMAAAANAAAAAA0CAAAAAUAAAAAAAAAAAAAADgAAAFcAAAAOAAAAWAAAAA0BAAAADgAAAGEAAAAOAAAAYgAAAA0DAAAADQIAAAABQAgAAAAAAAAAAAANAQAAAA4AAABmAAAADgAAAGUAAAAeAAAADQEAAAAOAAAAYgAAAA4AAABhAAAAAUAAAAAAAAAAAAAAHwAAAABfAANmMjEAO2ExMSoodC14Q29vcmQyKV4zK2IxMSoodC14Q29vcmQyKV4yK210MioodC14Q29vcmQyKSt5Q29vcmQyAAAADQAAAAANAAAAAA0AAAAADQIAAAAOAAAAawAAAB4AAAANAQAAACAAAAAAAAAADgAAAGEAAAABQAgAAAAAAAAAAAANAgAAAA4AAABsAAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAYQAAAAFAAAAAAAAAAAAAAA0CAAAADgAAAFcAAAANAQAAACAAAAAAAAAADgAAAGEAAAAOAAAAZQABdAAAABEAAAAAXwADYTEyAEUobXQzK210NCkvKHhDb29yZDQteENvb3JkMyleMisyKih5Q29vcmQzLXlDb29yZDQpLyh4Q29vcmQ0LXhDb29yZDMpXjMAAAANAAAAAA0DAAAADQAAAAAOAAAAWAAAAA4AAABZAAAAHgAAAA0BAAAADgAAAGMAAAAOAAAAYgAAAAFAAAAAAAAAAAAAAA0DAAAADQIAAAABQAAAAAAAAAAAAAANAQAAAA4AAABmAAAADgAAAGcAAAAeAAAADQEAAAAOAAAAYwAAAA4AAABiAAAAAUAIAAAAAAAAAAAAEQAAAABfAANiMTIARSgyKm10MyttdDQpLyh4Q29vcmQzLXhDb29yZDQpKzMqKHlDb29yZDQteUNvb3JkMykvKHhDb29yZDQteENvb3JkMyleMgAAAA0AAAAADQMAAAANAAAAAA0CAAAAAUAAAAAAAAAAAAAADgAAAFgAAAAOAAAAWQAAAA0BAAAADgAAAGIAAAAOAAAAYwAAAA0DAAAADQIAAAABQAgAAAAAAAAAAAANAQAAAA4AAABnAAAADgAAAGYAAAAeAAAADQEAAAAOAAAAYwAAAA4AAABiAAAAAUAAAAAAAAAAAAAAHwAAAABfAANmMzEAO2ExMioodC14Q29vcmQzKV4zK2IxMioodC14Q29vcmQzKV4yK210MyoodC14Q29vcmQzKSt5Q29vcmQzAAAADQAAAAANAAAAAA0AAAAADQIAAAAOAAAAbgAAAB4AAAANAQAAACAAAAAAAAAADgAAAGIAAAABQAgAAAAAAAAAAAANAgAAAA4AAABvAAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAYgAAAAFAAAAAAAAAAAAAAA0CAAAADgAAAFgAAAANAQAAACAAAAAAAAAADgAAAGIAAAAOAAAAZgABdAAAAB8AAAAAXwADZjEzAFModDx4Q29vcmQyKSpmMTEodCkrKHQ+PXhDb29yZDIpKih0PHhDb29yZDMpKmYyMSh0KSsodD49eENvb3JkMykqKHQ8PXhDb29yZDQpKmYzMSh0KQAAAA0AAAAADQAAAAANAgAAAA0EAAAAIAAAAAAAAAAOAAAAYf####8AAAABAA5DQXBwZWxGb25jdGlvbgAAAGoAAAAgAAAAAAAAAA0CAAAADQIAAAANBwAAACAAAAAAAAAADgAAAGEAAAANBAAAACAAAAAAAAAADgAAAGIAAAAhAAAAbQAAACAAAAAAAAAADQIAAAANAgAAAA0HAAAAIAAAAAAAAAAOAAAAYgAAAA0GAAAAIAAAAAAAAAAOAAAAYwAAACEAAABwAAAAIAAAAAAAAXQAAAAYAAAAAF8AB3hDb29yZDUAAAAKAAAAUQAAABgAAAAAXwAHeENvb3JkNgAAAAoAAAABAAAAGAAAAABfAAd4Q29vcmQ3AAAACgAAAFIAAAAYAAAAAF8AB3hDb29yZDgAAAAKAAAAUwAAABoAAAAAXwAHeUNvb3JkNQAAAAoAAABRAAAAGgAAAABfAAd5Q29vcmQ2AAAACgAAAAEAAAAaAAAAAF8AB3lDb29yZDcAAAAKAAAAUgAAABoAAAAAXwAHeUNvb3JkOAAAAAoAAABTAAAAEQAAAABfAAJhMQBFKG10NCttdDUpLyh4Q29vcmQ2LXhDb29yZDUpXjIrMiooeUNvb3JkNS15Q29vcmQ2KS8oeENvb3JkNi14Q29vcmQ1KV4zAAAADQAAAAANAwAAAA0AAAAADgAAAFkAAAAOAAAAWgAAAB4AAAANAQAAAA4AAABzAAAADgAAAHIAAAABQAAAAAAAAAAAAAANAwAAAA0CAAAAAUAAAAAAAAAAAAAADQEAAAAOAAAAdgAAAA4AAAB3AAAAHgAAAA0BAAAADgAAAHMAAAAOAAAAcgAAAAFACAAAAAAAAAAAABEAAAAAXwABYgBFKDIqbXQ0K210NSkvKHhDb29yZDUteENvb3JkNikrMyooeUNvb3JkNi15Q29vcmQ1KS8oeENvb3JkNi14Q29vcmQ1KV4yAAAADQAAAAANAwAAAA0AAAAADQIAAAABQAAAAAAAAAAAAAAOAAAAWQAAAA4AAABaAAAADQEAAAAOAAAAcgAAAA4AAABzAAAADQMAAAANAgAAAAFACAAAAAAAAAAAAA0BAAAADgAAAHcAAAAOAAAAdgAAAB4AAAANAQAAAA4AAABzAAAADgAAAHIAAAABQAAAAAAAAAAAAAAfAAAAAF8AA2YyMgA4YTEqKHQteENvb3JkNSleMytiKih0LXhDb29yZDUpXjIrbXQ0Kih0LXhDb29yZDUpK3lDb29yZDUAAAANAAAAAA0AAAAADQAAAAANAgAAAA4AAAB6AAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAcgAAAAFACAAAAAAAAAAAAA0CAAAADgAAAHsAAAAeAAAADQEAAAAgAAAAAAAAAA4AAAByAAAAAUAAAAAAAAAAAAAADQIAAAAOAAAAWQAAAA0BAAAAIAAAAAAAAAAOAAAAcgAAAA4AAAB2AAF0AAAAEQAAAABfAAJhMgBFKG10NSttdDYpLyh4Q29vcmQ3LXhDb29yZDYpXjIrMiooeUNvb3JkNi15Q29vcmQ3KS8oeENvb3JkNy14Q29vcmQ2KV4zAAAADQAAAAANAwAAAA0AAAAADgAAAFoAAAAOAAAAWwAAAB4AAAANAQAAAA4AAAB0AAAADgAAAHMAAAABQAAAAAAAAAAAAAANAwAAAA0CAAAAAUAAAAAAAAAAAAAADQEAAAAOAAAAdwAAAA4AAAB4AAAAHgAAAA0BAAAADgAAAHQAAAAOAAAAcwAAAAFACAAAAAAAAAAAABEAAAAAXwACYjIARSgyKm10NSttdDYpLyh4Q29vcmQ2LXhDb29yZDcpKzMqKHlDb29yZDcteUNvb3JkNikvKHhDb29yZDcteENvb3JkNileMgAAAA0AAAAADQMAAAANAAAAAA0CAAAAAUAAAAAAAAAAAAAADgAAAFoAAAAOAAAAWwAAAA0BAAAADgAAAHMAAAAOAAAAdAAAAA0DAAAADQIAAAABQAgAAAAAAAAAAAANAQAAAA4AAAB4AAAADgAAAHcAAAAeAAAADQEAAAAOAAAAdAAAAA4AAABzAAAAAUAAAAAAAAAAAAAAHwAAAABfAANmMjMAOWEyKih0LXhDb29yZDYpXjMrYjIqKHQteENvb3JkNileMittdDUqKHQteENvb3JkNikreUNvb3JkNgAAAA0AAAAADQAAAAANAAAAAA0CAAAADgAAAH0AAAAeAAAADQEAAAAgAAAAAAAAAA4AAABzAAAAAUAIAAAAAAAAAAAADQIAAAAOAAAAfgAAAB4AAAANAQAAACAAAAAAAAAADgAAAHMAAAABQAAAAAAAAAAAAAANAgAAAA4AAABaAAAADQEAAAAgAAAAAAAAAA4AAABzAAAADgAAAHcAAXQAAAARAAAAAF8AAmEzAEUobXQ2K210NykvKHhDb29yZDgteENvb3JkNyleMisyKih5Q29vcmQ3LXlDb29yZDgpLyh4Q29vcmQ4LXhDb29yZDcpXjMAAAANAAAAAA0DAAAADQAAAAAOAAAAWwAAAA4AAABcAAAAHgAAAA0BAAAADgAAAHUAAAAOAAAAdAAAAAFAAAAAAAAAAAAAAA0DAAAADQIAAAABQAAAAAAAAAAAAAANAQAAAA4AAAB4AAAADgAAAHkAAAAeAAAADQEAAAAOAAAAdQAAAA4AAAB0AAAAAUAIAAAAAAAAAAAAEQAAAABfAAJiMwBFKDIqbXQ2K210NykvKHhDb29yZDcteENvb3JkOCkrMyooeUNvb3JkOC15Q29vcmQ3KS8oeENvb3JkOC14Q29vcmQ3KV4yAAAADQAAAAANAwAAAA0AAAAADQIAAAABQAAAAAAAAAAAAAAOAAAAWwAAAA4AAABcAAAADQEAAAAOAAAAdAAAAA4AAAB1AAAADQMAAAANAgAAAAFACAAAAAAAAAAAAA0BAAAADgAAAHkAAAAOAAAAeAAAAB4AAAANAQAAAA4AAAB1AAAADgAAAHQAAAABQAAAAAAAAAAAAAAfAAAAAF8AA2YyNAA5YTMqKHQteENvb3JkNyleMytiMyoodC14Q29vcmQ3KV4yK210NioodC14Q29vcmQ3KSt5Q29vcmQ3AAAADQAAAAANAAAAAA0AAAAADQIAAAAOAAAAgAAAAB4AAAANAQAAACAAAAAAAAAADgAAAHQAAAABQAgAAAAAAAAAAAANAgAAAA4AAACBAAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAdAAAAAFAAAAAAAAAAAAAAA0CAAAADgAAAFsAAAANAQAAACAAAAAAAAAADgAAAHQAAAAOAAAAeAABdAAAAB8AAAAAXwADZjI1AGAodD49eENvb3JkNSkqKHQ8eENvb3JkNikqZjIyKHQpKyh0Pj14Q29vcmQ2KSoodDx4Q29vcmQ3KSpmMjModCkrKHQ+PXhDb29yZDcpKih0PD14Q29vcmQ4KSpmMjQodCkAAAANAAAAAA0AAAAADQIAAAANAgAAAA0HAAAAIAAAAAAAAAAOAAAAcgAAAA0EAAAAIAAAAAAAAAAOAAAAcwAAACEAAAB8AAAAIAAAAAAAAAANAgAAAA0CAAAADQcAAAAgAAAAAAAAAA4AAABzAAAADQQAAAAgAAAAAAAAAA4AAAB0AAAAIQAAAH8AAAAgAAAAAAAAAA0CAAAADQIAAAANBwAAACAAAAAAAAAADgAAAHQAAAANBgAAACAAAAAAAAAADgAAAHUAAAAhAAAAggAAACAAAAAAAAF0AAAAHwAAAABfAANmMTIAMyh0PD14Q29vcmQ0KSpmMTModCkrKHQ+eENvb3JkNCkqKHQ8PXhDb29yZDgpKmYyNSh0KQAAAA0AAAAADQIAAAANBgAAACAAAAAAAAAADgAAAGMAAAAhAAAAcQAAACAAAAAAAAAADQIAAAANAgAAAA0FAAAAIAAAAAAAAAAOAAAAYwAAAA0GAAAAIAAAAAAAAAAOAAAAdQAAACEAAACDAAAAIAAAAAAAAXQAAAAYAAAAAF8AB3hDb29yZDkAAAAKAAAAVAAAABoAAAAAXwAHeUNvb3JkOQAAAAoAAABUAAAAEQAAAABfAAJhNABFKG10NyttdDgpLyh4Q29vcmQ5LXhDb29yZDgpXjIrMiooeUNvb3JkOC15Q29vcmQ5KS8oeENvb3JkOS14Q29vcmQ4KV4zAAAADQAAAAANAwAAAA0AAAAADgAAAFwAAAAOAAAAXQAAAB4AAAANAQAAAA4AAACFAAAADgAAAHUAAAABQAAAAAAAAAAAAAANAwAAAA0CAAAAAUAAAAAAAAAAAAAADQEAAAAOAAAAeQAAAA4AAACGAAAAHgAAAA0BAAAADgAAAIUAAAAOAAAAdQAAAAFACAAAAAAAAAAAABEAAAAAXwACYjQARSgyKm10NyttdDgpLyh4Q29vcmQ4LXhDb29yZDkpKzMqKHlDb29yZDkteUNvb3JkOCkvKHhDb29yZDkteENvb3JkOCleMgAAAA0AAAAADQMAAAANAAAAAA0CAAAAAUAAAAAAAAAAAAAADgAAAFwAAAAOAAAAXQAAAA0BAAAADgAAAHUAAAAOAAAAhQAAAA0DAAAADQIAAAABQAgAAAAAAAAAAAANAQAAAA4AAACGAAAADgAAAHkAAAAeAAAADQEAAAAOAAAAhQAAAA4AAAB1AAAAAUAAAAAAAAAAAAAAHwAAAABfAANmMjYAOWE0Kih0LXhDb29yZDgpXjMrYjQqKHQteENvb3JkOCleMittdDcqKHQteENvb3JkOCkreUNvb3JkOAAAAA0AAAAADQAAAAANAAAAAA0CAAAADgAAAIcAAAAeAAAADQEAAAAgAAAAAAAAAA4AAAB1AAAAAUAIAAAAAAAAAAAADQIAAAAOAAAAiAAAAB4AAAANAQAAACAAAAAAAAAADgAAAHUAAAABQAAAAAAAAAAAAAANAgAAAA4AAABcAAAADQEAAAAgAAAAAAAAAA4AAAB1AAAADgAAAHkAAXQAAAAfAAAAAF8AAmYxACYodDw9eENvb3JkOCkqZjEyKHQpKyh0PnhDb29yZDgpKmYyNih0KQAAAA0AAAAADQIAAAANBgAAACAAAAAAAAAADgAAAHUAAAAhAAAAhAAAACAAAAAAAAAADQIAAAANBQAAACAAAAAAAAAADgAAAHUAAAAhAAAAiQAAACAAAAAAAAF0AAAAGAAAAABfAAh4Q29vcmQxMAAAAAoAAABVAAAAGgAAAABfAAh5Q29vcmQxMAAAAAoAAABVAAAAEQAAAABfAAJhNQBIKG10OCttdDkpLyh4Q29vcmQxMC14Q29vcmQ5KV4yKzIqKHlDb29yZDkteUNvb3JkMTApLyh4Q29vcmQxMC14Q29vcmQ5KV4zAAAADQAAAAANAwAAAA0AAAAADgAAAF0AAAAOAAAAXgAAAB4AAAANAQAAAA4AAACLAAAADgAAAIUAAAABQAAAAAAAAAAAAAANAwAAAA0CAAAAAUAAAAAAAAAAAAAADQEAAAAOAAAAhgAAAA4AAACMAAAAHgAAAA0BAAAADgAAAIsAAAAOAAAAhQAAAAFACAAAAAAAAAAAABEAAAAAXwACYjUASCgyKm10OCttdDkpLyh4Q29vcmQ5LXhDb29yZDEwKSszKih5Q29vcmQxMC15Q29vcmQ5KS8oeENvb3JkMTAteENvb3JkOSleMgAAAA0AAAAADQMAAAANAAAAAA0CAAAAAUAAAAAAAAAAAAAADgAAAF0AAAAOAAAAXgAAAA0BAAAADgAAAIUAAAAOAAAAiwAAAA0DAAAADQIAAAABQAgAAAAAAAAAAAANAQAAAA4AAACMAAAADgAAAIYAAAAeAAAADQEAAAAOAAAAiwAAAA4AAACFAAAAAUAAAAAAAAAAAAAAHwAAAABfAAJmMgA5YTUqKHQteENvb3JkOSleMytiNSoodC14Q29vcmQ5KV4yK210OCoodC14Q29vcmQ5KSt5Q29vcmQ5AAAADQAAAAANAAAAAA0AAAAADQIAAAAOAAAAjQAAAB4AAAANAQAAACAAAAAAAAAADgAAAIUAAAABQAgAAAAAAAAAAAANAgAAAA4AAACOAAAAHgAAAA0BAAAAIAAAAAAAAAAOAAAAhQAAAAFAAAAAAAAAAAAAAA0CAAAADgAAAF0AAAANAQAAACAAAAAAAAAADgAAAIUAAAAOAAAAhgABdAAAAB8BAAAAXwABZwAkKHQ8PXhDb29yZDkpKmYxKHQpKyh0PnhDb29yZDkpKmYyKHQpAAAADQAAAAANAgAAAA0GAAAAIAAAAAAAAAAOAAAAhQAAACEAAACKAAAAIAAAAAAAAAANAgAAAA0FAAAAIAAAAAAAAAAOAAAAhQAAACEAAACPAAAAIAAAAAAAAXQAAAAXAP####8AAAAAABAAAAEAAAABAAAATgAAAFUAAAAEAP####8BAAAAABAAAngxAAAAAAAAAAAAQAgAAAAAAAAAAAUAAQAAAAAAAAAAAAAAkQAAABgA#####wACeDEAAAAKAAAAkgAAABEA#####wACeTEABWcoeDEpAAAAIQAAAJAAAAAOAAAAkwAAABYA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAACgAAAA4AAACTAAAADgAAAJT#####AAAAAgANQ0xpZXVEZVBvaW50cwD#####AAAA#wAAAAIAAACVAAAB9AABAAAAkgAAAAQAAACSAAAAkwAAAJQAAACVAAAADv##########
Nous allons quand même expliquer comment cette figure a été construite.
On a d'abord utilisé l'icône  de création d'une nouvelle figure et choisi de créer une Figure avec repère.
de création d'une nouvelle figure et choisi de créer une Figure avec repère.
Les calculs suivants ont été créés :
| Nom du calcul | Formule |
|---|---|
| nbvar | 5 |
| nbcas1 | 2 |
| nbcas2 | 2 |
| nbcas3 | 2 |
| nbcas4 | 3 |
| nbcas5 | 7 |
| r1 | int(rand(0)*nbcas1) |
| r2 | int(rand(0)*nbcas2) |
| r3 | int(rand(0)*nbcas3) |
| r4 | int(rand(0)*nbcas4) |
| r5 | int(rand(0)*nbcas5) |
La création de ces calculs est indispensable pour que la ressource j3p associée donne lors des répétitions successives des valeurs à r1, r2, …, r5 toutes distinctes les unes des autres.
Par exemple il sera donné à r1 des valeurs distinctes successives comprises entre 0 et 1 lors des répétitions (car nbcas1 est égal à 2) et à r5 des valeurs distinctes successives comprises entre 0 et 6 (car nbcas5 est égal à 7).
Les formules que nous mettons dans r1, r2, …, r5 ne servent donc qu'à simuler les formules qui seront mises dans ces calculs lors des répétitions successives.
Ensuite les calculs suivants ont été créés :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| k | 2+r1 | k pourra donc prendre deux valeurs : 2 et 3 |
| p | -3-r2 | p pourra prendre les valeurs -3 et -4 |
| q | -2-r3 | q pourra prendre les valeurs -2 et -3 |
| a | (r4=0)*(-5)+(r4=1)+(r4=2)*5 | a pourra prendre les valeurs -5, 1 ou 5 |
| f | 1+r5 | f pourra prendre les valeurs entières de 1 à 7. Les valeurs de f correspondront aux 7 questions différentes qui pourront être posées à l'élève. |
Ensuite, avec l'outil  ont été créés 8 points :
ont été créés 8 points :
| Point n° | Coordonnées |
|---|---|
| 1 | (-6; 0) |
| 2 | (-5; k) |
| 3 | (-4; 0) |
| 4 | (q; p) |
| 6 | (1; k) |
| 7 | (3; k+1) |
| 8 | (5; k) |
| 9 | (7; 0) |
L'outil qui a été utilisé pour créer la courbe est l'outil  qui permet de créer une courbe passant par des points donnés. Ici la courbe est créée à partir de neufs points : les 8 points ci-dessus, l'origine de repère ayant été choisie comme point n°5.
qui permet de créer une courbe passant par des points donnés. Ici la courbe est créée à partir de neufs points : les 8 points ci-dessus, l'origine de repère ayant été choisie comme point n°5.
Lorsqu'on a utilisé cet outil, on a d'abord précisé qu'il y avait neuf points, on a cliqué sur ces points dans l'ordre ci-dessus (l'origine étant le cinquième point) et on a spécifié ensuite les coefficients directeurs des tangentes à ces points dans une boîte de dialogue.
| Point n° | Coordonnées | Coefficient directeur de la tangente |
|---|---|---|
| 1 | (-6; 0) | 3 |
| 2 | (-5; k) | 0 |
| 3 | (-4; 0) | -3 |
| 4 | (q; p) | 0 |
| 5 | (0; 0) | 2 |
| 6 | (1; k) | 1 |
| 7 | (3; k+1) | 0 |
| 8 | (5; k) | -1 |
| 9 | (7; 0) | -1 |
Quand on a fini, la courbe apparaît. Il s'agit en fait du résultat d'une macro-construction.
La fonction créée par la macro construction a ensuite été renommée g.
Cette courbe étant tracée sur R, on l'a détruite, et ensuite, en trait bleu et épais de deux pixels, on a créé la courbe de g restreinte à l'intervalle [-6; 7] avec l'outil  (en cochant courbe à tracer sur ][a;b][ et en entrant -6 comme valeur pour a et 7 pour valeur de b).
(en cochant courbe à tracer sur ][a;b][ et en entrant -6 comme valeur pour a et 7 pour valeur de b).
Ensuite le nom des points servant à définir la courbe a été masqué à l'aide de l'icône ![]() (sauf pour l'origine 0).
(sauf pour l'origine 0).
Maintenant vous allez créer avec l'outil ![]() les 7 calculs réels suivants :
les 7 calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| form1 | f=1 | Vaut 1 si f = 1 et 0 sinon |
| form2 | f=2 | Vaut 1 si f = 2 et 0 sinon |
| form3 | f=3 | Vaut 1 si f = 3 et 0 sinon |
| form4 | f=4 | Vaut 1 si f = 4 et 0 sinon |
| form5 | f=5 | Vaut 1 si f = 5 et 0 sinon |
| form6 | f=6 | Vaut 1 si f = 6 et 0 sinon |
| form7 | f=7 | Vaut 1 si f = 7 et 0 sinon |
Nous allons créer un premier affichage LaTeX dontle contenu sera la consigne initiale.
Utilisez donc l'outil ![]() de création d'un affichage libre (en déroulant la barre d'outils des affichages) et cliquez par exemple en haut et à droite de la figure.
de création d'un affichage libre (en déroulant la barre d'outils des affichages) et cliquez par exemple en haut et à droite de la figure.
Voici le code LaTex que vous devez entre dans la boîte de dialogue :
\begin{array}{l}
\text{On considère la fonction $f$ définie sur [-6;7] dont la courbe représentative est tracée ci-dessous.
}
\\ \text{Cliquer sur le bouton OK ou taper sur la touche Entrée pour valider la réponse.}
\end{array}
Le code LaTeX doit renvoyer un ou plusieurs éléments \text donc le contenu est ce qui sera affiché dans la consigne.
Ici nous avons cliqué sur l'icône pour avoir une matrice colonne et complété pour avoir deux lignes, chacune étant composée d'un champ LaTeX \text{} dont le contenu est chaque ligne qui sera affichée dans la consigne (ici deux lignes). A l'intérieur de chacun de ces champs \text on entoure de deux $ ce qui devra être affiché en mode maths. Ainsi par exemple $f$ affichera la lettre f en italique.
Nous devons maintenant donner un tag à cet affichage LaTeX.
Pour cela utilisez dans la barre d'outils supérieure l'outil ![]() et sélectionnez le dernier élément de la liste des objets (qui est nommé lat1 dans le protocole).
et sélectionnez le dernier élément de la liste des objets (qui est nommé lat1 dans le protocole).
Cliquez sur le bouton Changer le tag et, dans la boîte de dialogue qui s'ouvre, entrez comme tag enonce.
Le formulaire que l'élève devra remplir va dépendre des valeurs prises par f.
Il doit donc être dynamique et sera compris dans un affichage LaTeX que nous allons créer. Cet affichage LaTeX doit avoir pour tag formulaire
Utilisez donc l'outil ![]() de création d'un affichage libre (en déroulant la barre d'outils des affichages) et cliquez par exemple en bas et à droite de la figure.
de création d'un affichage libre (en déroulant la barre d'outils des affichages) et cliquez par exemple en bas et à droite de la figure.
Le code LaTeX doit renvoyer un ou plusieurs éléments \text donc le contenu est ce qui sera affiché dans la consigne.
Ici nous utilisons des affichages LaTeX conditionnels puisque la question dépend des valeurs de f.
Voici ci-dessous le contenu LaTeX de cet affichage que vous pouvez coller dans la boîte de dialogue :
\If{form1}
{
\text{\Val{a} est list1 de \Val{k} par $f$}
}
{
\If{form2}
{
\text{Un antécédent de 0 par $f$ est edit1}
}
{
\If{form3}
{
\text{\Val{k} est list1 de \Val{a} par $f$}
}
{
\If{form4}
{
\text{\Val{k} admet edit1 antécédents par $f$}
}
{
\If{form5}
{
\text{Un nombre ayant exactement 4 antécédents par $f$ est edit1}
}
{
\If{form6}
{
\text{Un nombre ayant exactement 2 antécédents par $f$ est edit1}
}
{
\text{Un nombre ayant un seul antécédent par $f$ est edit1}
}
}
}
}
}
}
Nous devons maintenant donner un tag à cet affichage LaTeX.
Pour cela utilisez dans la barre d'outils supérieure l'outil ![]() et sélectionnez le dernier élément de la liste des objets (qui est nommé lat2 dans le protocole).
et sélectionnez le dernier élément de la liste des objets (qui est nommé lat2 dans le protocole).
Cliquez sur le bouton Changer le tag et, dans la boîte de dialogue qui s'ouvre, entrez comme tag formulaire.
Fermez la boîte de dialogue du protocole.
Un autre affichage LaTeX va contenir, lui, les items que doit proposer la liste déroulante utilisée dans la consigne renvoyée par l'affichage ci-dessus.
Utilisez de nouveau l'outil ![]() de création d'une affichage libre (en déroulant la barre d'outils des affichages) et cliquez au voisinage de l'affichage LaTeX précédent.
de création d'une affichage libre (en déroulant la barre d'outils des affichages) et cliquez au voisinage de l'affichage LaTeX précédent.
Entrez comme code LaTeX le code ci-dessous :
\If{form1}
{
\begin{array}{l}
\text{un antécédent }
\\ \text{l'image }
\end{array}
}
{
\If{form3}
{
\begin{array}{l}
\text{l'image}
\\ \text{un antécédent}
\end{array}
}
{
}
}
Cet affichage LaTeX utilise lui-aussi des affichages conditionnels.
Pour que tout se passe bien, il faut maintenant donner un tag à ce dernier affichage LaTeX.
Utilisez dans la barre d'outils supérieure l'outil ![]() et sélectionnez le dernier élément de la liste des objets (qui est nommé lat2 dans le protocole).
et sélectionnez le dernier élément de la liste des objets (qui est nommé lat2 dans le protocole).
Cliquez sur le bouton Changer le tag et, dans la boîte de dialogue qui s'ouvre, entrez comme tag list1.
Fermez la boîte de dialogue de protocole.
Il est recommandé de sauvegarder votre figure de temps en temps avec l'outil ![]() .
.
Expliquons comment cela marche.
Quand nous allons paramétrer notre ressource, le paramètre formulaire contiendra une chaîne vide, ce qui signifie que le formulaire est rendu dans l'affichage LaTeX de la figure qui a pour tag formulaire.
Imaginons que, par exemple, la valeur de f soit égale à 3.
Avec notre affichage conditionnel, comme form3 vaut 1, notre premier affichage LaTeX renvoie comme code LaTeX :
\text{\Val{k} est list1 de \Val{a} par $f$}
Ce qui sera utilisé pour écrire le formulaire à compléter par l'élève sera alors le contenu du \text :
\Val{k} est list1 de \Val{a} par $f$
où \Val{a} sera remplacé par la valeur actuelle du calcul a.
$f$ provoquera l'affichage de la lettre f en italique (car ce sera un affichage LaTeX).
list1 sera remplacé par une liste déroulante donc le premier élément sera … et les deux éléments suivants seront cherchés dans l'affichage LaTeX de tag list1.
Or, si f=3, cet affichage LaTex rend le code LaTeX suivant :
\begin{array}{l}
\text{L'image}
\\ \text{Un antécédent}
\end{array}
On affectera alors comme deuxièmes et troisièmes items de la liste déroulante les contenus des champs \text contenus dans cet affichage LaTeX, soit : l'image comme deuxième item et un antécédent comme troisième item.
Lorsque l'exercice se déroulera, si f a la valeur 3, la question posée pourra ressembler, une fois la liste déroulée, à ceci :
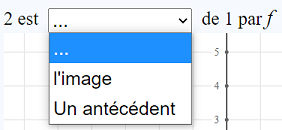 .
.
Vous pouvez maintenant utiliser l'icône ![]() pour masquer ces deux affichages LaTeX.
pour masquer ces deux affichages LaTeX.
Il nous faut maintenant définir deux calculs chargés de donner les réponses attendues dans la liste déroulante et dans les éditeurs numériques.
Créez les calculs numériques suivants :
Un calcul nommé rep1 qui contiendra la réponse de l'élève dans le champ numérique quand il fait partie du formulaire.
Un calcul nommé exact1 avec comme formule :
si(form2,rep1=-6|rep1=-4|rep1=0|rep1=7,si(form4,rep1=3,si(form5,rep1<k&rep1>=0,si(form6,rep1<0&rep1>p|rep1>k&rep1<k+1,si(form7,rep1=p|rep1=k+1,0)))))
</code>
Un calcul nommé resolu1 contenant comme formule exact1
Ce calcul doit contenir 1 si la réponse du champ numérique 1 (il n'y a en fait qu'un champ numérique) est égale à une des valeurs attendues.
Dans cet exercice, une formule contenant la bonne valeur sera considérée comme exacte, même si la formule n'est pas simplifiée.
Si ce n'était pas le cas, resolu1 devrait ne contenir 1 que si la réponse dans rep1 est bien simplifiée.
Créez enfin un calcul nommé reslist1 contenant comme formule :
si(form1|form3,1,0)
Le résultat renvoyé par reslist1 doit le numéro de l'item de la liste qui correspond à la bonne réponse (ici 1 dans le cas où notre formulaire contient une liste car c'est le premier des deux items qui est la bonne réponse).
Pour finir, lors de la correction , nous allons donner à l'élève la possibilité de visualiser la notion d'antécédent.
Nous allons maintenant créer des objets qui seront affichés lors de la correction.
Dans la palette des couleurs, activez la couleur marron et activez dans la palette de style de point le rond de taille moyenne.
Utilisez l'icône ![]() pour créer un point lié à l'axe des ordonnées dont l'ordonnée soit comprise entre 0 et 1 (de façon qu'il y ait 4 antécédents) et nommez ce point m.
pour créer un point lié à l'axe des ordonnées dont l'ordonnée soit comprise entre 0 et 1 (de façon qu'il y ait 4 antécédents) et nommez ce point m.
Utilisez l'icône ![]() pour que le nom de ce point soit masqué.
pour que le nom de ce point soit masqué.
Maintenant à l'aide de l'outil ![]() de mesure d'ordonnée dans un repère, créez la mesure de l'ordonnée de m dans notre repère. Comme nom pour cette mesure choisissez m.
de mesure d'ordonnée dans un repère, créez la mesure de l'ordonnée de m dans notre repère. Comme nom pour cette mesure choisissez m.
Utilisez l'icône ![]() pour créer la parallèle à l'axe des abscisses passant par m.
pour créer la parallèle à l'axe des abscisses passant par m.
Pour gérer les problèmes d'arrondis nous allons créer une fonction réelle nommé zero et un calcul nommé m'.
Utilisez l'icône ![]() pour créer la fonction nommée zero avec comme variable formelle x et comme formule :
pour créer la fonction nommée zero avec comme variable formelle x et comme formule :
abs(x)<=0.01
Prenez garde de décocher la case Tracer courbe dans la boîte de dialogue avant de valider.
Utilisez l'outil ![]() pour créer un calcul nommé m' avec comme formule :
pour créer un calcul nommé m' avec comme formule :
si(zero(m-k),k,si(zero(m-p),p,si(zero(m-k-1),k+1,m)))
Ce calcul m' nous sert à arrondir la valeur de m quand on est proche d'un maximum ou d'un minimum de la fonction.
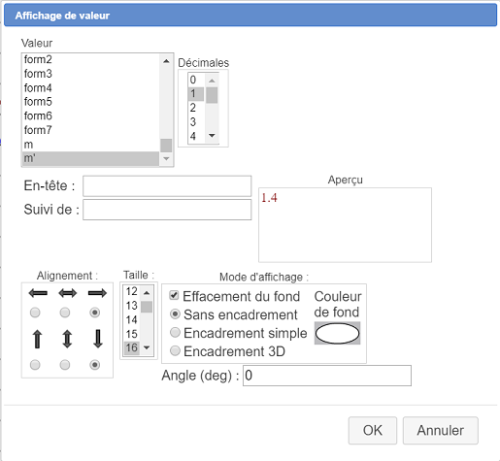
Nous allons maintenant créer un affichage de la valeur de m' lié au point m .
Pour cela, en déroulant la barre des outils d'affichage, cliquez sur l'outil ![]() (affichage de valeur lié à un point).
(affichage de valeur lié à un point).
Cliquez sur le point m.
Puis remplissez la boîte de dialogue comme ci-dessous :
Vous pouvez ensuite décaler légèrement cet affichage à l'aide de l'outil de capture.
Nous désirons maintenant visualiser les antécédents de m par la fonction f.
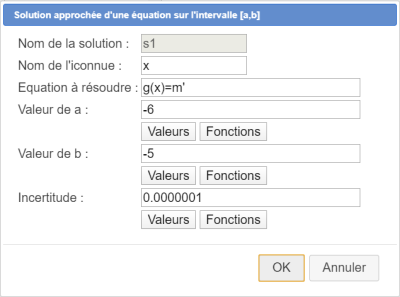
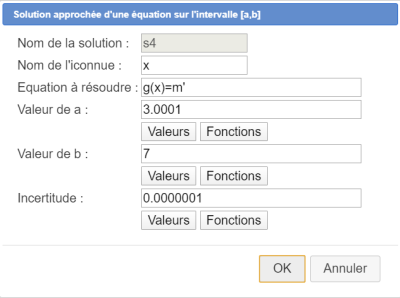
En déroulant la barre des outils de calcul, utilisez l'icône ![]() de création de solution approchée d'équation et remplissez la boîte de dialogue comme ci-dessous :
de création de solution approchée d'équation et remplissez la boîte de dialogue comme ci-dessous :
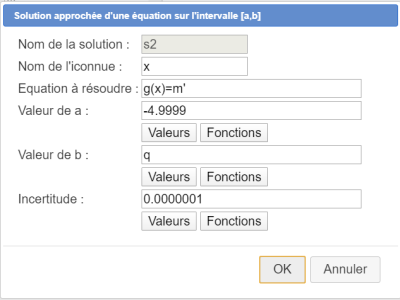
A l'aide de ce même outil, créez une deuxième valeur approchée de solution d'équation nommée s2:
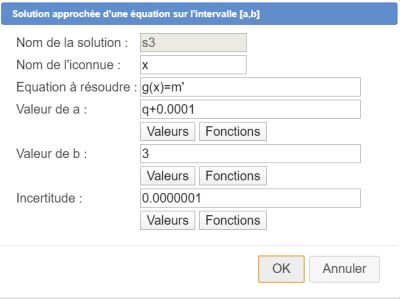
De même une autre nommé s3 :
Et une dernière nommé s4 :
Maintenant activez la couleur rouge et utilisez l'icône ![]() pour créer les points de coordonnées (s1, m), (s2, m), (s3,m), (s4, m), (s1, 0), (s2, 0), (s3,0), (s4, 0).
pour créer les points de coordonnées (s1, m), (s2, m), (s3,m), (s4, m), (s1, 0), (s2, 0), (s3,0), (s4, 0).
Dans la palette de style de trait, utilisez le style de trait pointillé et activez la couleur noire.
Utilisez l'icône ![]() pour joindre deux à deux ces derniers points en joignant les points de la courbe avec leurs projetés orthogonaux sur l'axe des abscisses.
pour joindre deux à deux ces derniers points en joignant les points de la courbe avec leurs projetés orthogonaux sur l'axe des abscisses.
Nous voulons maintenant pouvoir afficher le nombre d'antécédents de m par la fonction f.
Pour cela nous allons créer quatre tests d'existence en cliquant sur l'icône ![]() à droite de la barre d'outils de calculs puis en choisissant dans la liste proposée Test d'existence.
à droite de la barre d'outils de calculs puis en choisissant dans la liste proposée Test d'existence.
Créez les test suivants :
| Nom du test | Test d'existence de |
|---|---|
| t1 | s1 |
| t2 | s2 |
| t3 | s3 |
| t4 | s4 |
Par exemple t1 vaut 1 si s1 existe et 0 sinon.
Puis, avec l'outil ![]() créez un calcul nommé nbs avec comme formule :
créez un calcul nommé nbs avec comme formule :
t1+t2+t3+t4
Maintenant, activez la couleur marron et activez l'icône ![]() pour créer en bas et à droite de la figure un affichage LaTeX dont le code LaTeX soit le suivant (cochez la case Effacement du fond) :
pour créer en bas et à droite de la figure un affichage LaTeX dont le code LaTeX soit le suivant (cochez la case Effacement du fond) :
\begin{array}{l}
\text{L'équation }f(x)=\Val{m',2} \text{ admet }\Val{nbs}\text{ solution(s)}
\\ \Val{m',2} \text{ admet }\Val{nbs} \text{ antécédent(s) par }f.
\end{array}
Maintenant nous allons créer une macro dont l'objet sera de faire apparaître tous nos éléments de correction. Son intitulé doit être solution.
Pour cela, déroulez la barre d'outils des affichages, cliquez sur l'icône ![]() et choisissez Macro d'apparition.
et choisissez Macro d'apparition.
Cliquez à un endroit libre de la figure. Une boîte de dialogue s'ouvre.
Entrez comme intitulé solution et validez.
Il vous est demandé de cliquer sur les objets que la macro doit faire apparaître.
Cliquez sur :
Le point m, l'affichage de valeur de m' qui lui est lié, la droite horizontale, les quatre points d'intersection avec la courbe, leurs quatre projetés orthogonaux, les segments verticaux pointillés et le dernier affichage LaTeX que nous venons de créer.
Pour finir déroulez de nouveau la barre d'outils des affichages, cliquez sur l'icône ![]() et choisissez Macro de masquage à partir d'une autre macro.
et choisissez Macro de masquage à partir d'une autre macro.
Cliquez au-dessous de la macro précédente.
Dans la boîte de dialogue qui s'ouvre entrez comme intitulé masquer la solution (la macro solution est déjà sélectionnée car c'est la seule) et validez.
Maintenant, dans la barre d'outil du haut, activez l'outil ![]() d'exécution de macro et cliquez sur la macro masquer solution. Nos éléments de solution sont maintenant masqués.
d'exécution de macro et cliquez sur la macro masquer solution. Nos éléments de solution sont maintenant masqués.
Il reste à masquer les deux macros avec l'outil ![]() .
.
Notre figure est prête. Enregistrez-là sous le nom de votre choix et à l'emplacement de votre choix.
Nous allons maintenant créer une autre figure plus simple qui sera chargée, elle, d'afficher des éléments de correction au-dessous de la figure principale.
Utiliser l'icône ![]() puis choisissez Figure sans repère et sans longueur unité.
puis choisissez Figure sans repère et sans longueur unité.
Utilisez l'icône ![]() de choix des options de la figure, cliquez sur le lien Couleur de fond de la figure et choisissez comme couleur de fond #f6fafe qui est la couleur de fond pour LaboMep.
de choix des options de la figure, cliquez sur le lien Couleur de fond de la figure et choisissez comme couleur de fond #f6fafe qui est la couleur de fond pour LaboMep.
Utilisez l'outil ![]() pour créer les calculs numériques suivants :
pour créer les calculs numériques suivants :
| Nom du calcul | Formule |
|---|---|
| a | -5 |
| k | 2 |
| p | -3 |
| q | -2 |
| f | 7 |
| form1 | form=1 |
| form2 | form=2 |
| form3 | form=3 |
| form4 | form=4 |
| form5 | form=5 |
| form6 | form=6 |
| form7 | form=7 |
| maxi | k+1 |
Maintenant activez la couleur noire et utilisez l'outil ![]() pour créer un affichage LaTeX libre dont le code LaTeX est le suivant :
pour créer un affichage LaTeX libre dont le code LaTeX est le suivant :
\If{form1}
{
\begin{array}{l}
\text{\Val{a} est un antécédent de \Val{k} par }f\text{ car }f(\Val{a})=\Val{k}.
\\ \Val{k}<f(\Val{k})<\Val{maxi} \text{ donc l'image de \Val{k} par }f\text{ ne peut pas être égale à }\Val{a}.
\end{array}}
{
\If{form2}
{
\begin{array}{l}
0 \text{ est l'image par }f\text{ des nombres } -6, -4, 0\text{ et }7.
\\ -6, -4, 0\text{ et }7 \text{ sont les quatre antécédents de 0 par }f.
\end{array}
}
{
\If{form3}
{
\begin{array}{l}
\Val{k}\text{ est l'image de }\Val{a} \text{ par }f.
\\ \Val{k} \text{ ne peut pas être un antécédent de }\Val{a} \text{ puisque }f(\Val{k})\ne \Val{a}.
\end{array}
}
{
\If{form4}
{
\Val{k} \text{ admet exactement 3 antécédents par }f\text{ qui sont -5, 1 et 5.}
}
{
\If{form5}
{
\begin{array}{l}
\text{Les nombres ayant exactement 4 antécédents par }f
\\ \text{sont les nombres }k \text{ tels que }0\le k < \Val{k}\text{ car la droite}
\\ \text{d'équation }y=k\text{ rencontre alors la courbe quatre fois.}
\end{array}
}
{
\If{form6}
{
\begin{array}{l}
\text{Les nombres ayant exactement 2 antécédents par }f
\\ \text{sont les nombres }k \text{ tels que }\Val{p} < k < 0 \text{ ou } \Val{k}<k<\Val{maxi}
\\ \text{car la droite d'équation }y=k\text{ rencontre alors la courbe deux fois.}
\end{array}
}
{
\begin{array}{l}
\text{Les deux seuls nombres ayant exactement un antécédent par }f
\\ \text{sont les nombres } \Val{p} \text{ et }\Val{maxi}\text{ car les deux seules droites horizontales}
\\\text{ne rencontrant la courbe qu'en un point sont les droites d'équations}
\\y=\Val{p} \text{ et }y=\Val{maxi}.
\end{array}
}
}
}
}
}
}
Il faut comprendre que, lorsque cette figure sera affichée au-dessous de la figure principale, il sera donné aux calculs a, k, p, q et f les valeurs qu'ils avaient dans la figure principale car, dans les paramètres de la ressource, nous mettrons dans le paramètre nommé param la chaîne de caractères akpqf.
Pour tester cette figure, vous pouvez changer à votre guise les valeurs de a, k, p, q et f mais f doit rester un entier compris entre 1 et 7.
Enregistrez cette figure de correction sous le nom de votre choix.
Etape 2 : Création de notre ressource dans LaboMep
Connectez vous à LaboMep avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).
Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez par exemple Maîtriser la notion d'image et d'antécédent.
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez les cases seconde et première.
Dans les champs Résumé et Description, entrez Pose des questions sur la notion d'image et d'antécédent..
En bas de la page, cliquez sur Créer la ressource.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour J3P.
Ensuite faites glisser Exercice de calcul multi-éditeurs dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ Titre entrez ce qui suit :
Maîtriser la notion d'image et d'antécédent
Dans le champ *nbrepetitions entrez la valeur 7.
Ouvrez la figure principale depuis l'endroit où vous l'aviez sauvegardée et utilisez l'icône ![]() d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
Collez ce code Base 64 dans le champ fig.
Dans le champ width entrez 750 (Largeur en pixels de la figure principale).
Dans le champ height entrez 400 (Hauteur en pixels de la figure principale).
Dans le champ param entrez afkpq ( ce sont les noms des calculs qui devront être récupérés de la figure principale pour les affecter à la figure de correction).
Dans le champ nbLatex entrez 0.
Dans le champ charset entrez 0123456789+-. (Ce sont les caractères autorisés dans les champs d'éditions numériques.
Mettez à false tous les boutons de btnPuis à btnLn.
Ouvrez la figure de correction, récupérez son code Base 64 et collez-le dans le champ figSol
Au besoin vous pouvez le récupérer ci-dessous :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcvb6#gEA#wEAAAAAAAAAAAP5AAAChwAAAQEAAAAAAAAAAQAAAA######AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AAFhAAItNf####8AAAABAAxDTW9pbnNVbmFpcmUAAAABQBQAAAAAAAAAAAACAP####8AAWsAATIAAAABQAAAAAAAAAAAAAACAP####8AAXAAAi0zAAAAAwAAAAFACAAAAAAAAAAAAAIA#####wABcQACLTIAAAADAAAAAUAAAAAAAAAAAAAAAgD#####AAFmAAE3AAAAAUAcAAAAAAAAAAAAAgD#####AAVmb3JtMQADZj0x#####wAAAAEACkNPcGVyYXRpb24I#####wAAAAEAD0NSZXN1bHRhdFZhbGV1cgAAAAUAAAABP#AAAAAAAAAAAAACAP####8ABWZvcm0yAANmPTIAAAAECAAAAAUAAAAFAAAAAUAAAAAAAAAAAAAAAgD#####AAVmb3JtMwADZj0zAAAABAgAAAAFAAAABQAAAAFACAAAAAAAAAAAAAIA#####wAFZm9ybTQAA2Y9NAAAAAQIAAAABQAAAAUAAAABQBAAAAAAAAAAAAACAP####8ABWZvcm01AANmPTUAAAAECAAAAAUAAAAFAAAAAUAUAAAAAAAAAAAAAgD#####AAVmb3JtNgADZj02AAAABAgAAAAFAAAABQAAAAFAGAAAAAAAAAAAAAIA#####wAFZm9ybTcAA2Y9NwAAAAQIAAAABQAAAAUAAAABQBwAAAAAAAAAAAACAP####8ABG1heGkAA2srMQAAAAQAAAAABQAAAAIAAAABP#AAAAAAAAD#####AAAAAgAGQ0xhdGV4AP####8AAAAAAQAA#####xJAGAAAAAAAAEAgo9cKPXCkAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAZPXElme2Zvcm0xfQp7ClxiZWdpbnthcnJheX17bH0KXHRleHR7XFZhbHthfSBlc3QgdW4gYW50w6ljw6lkZW50IGRlIFxWYWx7a30gcGFyIH1mXHRleHR7IGNhciB9ZihcVmFse2F9KT1cVmFse2t9LgpcXCBcVmFse2t9PGYoXFZhbHtrfSk8XFZhbHttYXhpfSBcdGV4dHsgZG9uYyBsJ2ltYWdlIGRlIFxWYWx7a30gcGFyIH1mXHRleHR7IG5lIHBldXQgcGFzIMOqdHJlIMOpZ2FsZSDDoCB9XFZhbHthfS4KXGVuZHthcnJheX19CnsKXElme2Zvcm0yfQp7ClxiZWdpbnthcnJheX17bH0KMCBcdGV4dHsgZXN0IGwnaW1hZ2UgcGFyIH1mXHRleHR7IGRlcyBub21icmVzIH0gLTYsIC00LCAwXHRleHR7IGV0IH03LgpcXCAtNiwgLTQsIDBcdGV4dHsgZXQgfTcgXHRleHR7IHNvbnQgbGVzIHF1YXRyZSBhbnTDqWPDqWRlbnRzIGRlIDAgcGFyIH1mLgpcZW5ke2FycmF5fQp9CnsKXElme2Zvcm0zfQp7ClxiZWdpbnthcnJheX17bH0KXFZhbHtrfVx0ZXh0eyBlc3QgbCdpbWFnZSBkZSB9XFZhbHthfSBcdGV4dHsgcGFyIH1mLgpcXCBcVmFse2t9IFx0ZXh0eyBuZSBwZXV0IHBhcyDDqnRyZSB1biBhbnTDqWPDqWRlbnQgZGUgfVxWYWx7YX0gXHRleHR7IHB1aXNxdWUgfWYoXFZhbHtrfSlcbmUgXFZhbHthfS4KXGVuZHthcnJheX0KfQp7ClxJZntmb3JtNH0KewpcVmFse2t9IFx0ZXh0eyBhZG1ldCBleGFjdGVtZW50IDMgYW50w6ljw6lkZW50cyBwYXIgfWZcdGV4dHsgcXVpIHNvbnQgLTUsIDEgZXQgNS59Cn0KewpcSWZ7Zm9ybTV9CnsKXGJlZ2lue2FycmF5fXtsfQpcdGV4dHtMZXMgbm9tYnJlcyBheWFudCBleGFjdGVtZW50IDQgYW50w6ljw6lkZW50cyBwYXIgfWYgClxcIFx0ZXh0e3NvbnQgbGVzIG5vbWJyZXMgfWsgXHRleHR7IHRlbHMgcXVlIH0wXGxlIGsgPCBcVmFse2t9XHRleHR7IGNhciBsYSBkcm9pdGV9ClxcIFx0ZXh0e2Qnw6lxdWF0aW9uIH15PWtcdGV4dHsgcmVuY29udHJlIGFsb3JzIGxhIGNvdXJiZSBxdWF0cmUgZm9pcy59ClxlbmR7YXJyYXl9Cn0KewpcSWZ7Zm9ybTZ9CnsKXGJlZ2lue2FycmF5fXtsfQpcdGV4dHtMZXMgbm9tYnJlcyBheWFudCBleGFjdGVtZW50IDIgYW50w6ljw6lkZW50cyBwYXIgfWYgClxcIFx0ZXh0e3NvbnQgbGVzIG5vbWJyZXMgfWsgXHRleHR7IHRlbHMgcXVlIH1cVmFse3B9IDwgayA8IDAgXHRleHR7IG91IH0gXFZhbHtrfTxrPFxWYWx7bWF4aX0gClxcIFx0ZXh0e2NhciBsYSBkcm9pdGUgZCfDqXF1YXRpb24gfXk9a1x0ZXh0eyByZW5jb250cmUgYWxvcnMgbGEgY291cmJlIGRldXggZm9pcy59ClxlbmR7YXJyYXl9Cn0KewpcYmVnaW57YXJyYXl9e2x9Clx0ZXh0e0xlcyBkZXV4IHNldWxzIG5vbWJyZXMgYXlhbnQgZXhhY3RlbWVudCB1biBhbnTDqWPDqWRlbnQgcGFyIH1mIApcXCBcdGV4dHtzb250IGxlcyBub21icmVzIH0gXFZhbHtwfSBcdGV4dHsgZXQgfVxWYWx7bWF4aX1cdGV4dHsgY2FyIGxlcyBkZXV4IHNldWxlcyBkcm9pdGVzIGhvcml6b250YWxlc30KXFxcdGV4dHtuZSByZW5jb250cmFudCBsYSBjb3VyYmUgcXUnZW4gdW4gcG9pbnQgc29udCBsZXMgZHJvaXRlcyBkJ8OpcXVhdGlvbnN9ClxceT1cVmFse3B9IFx0ZXh0eyBldCB9eT1cVmFse21heGl9LgpcZW5ke2FycmF5fQp9Cn0KfQp9Cn0Kff###############w==
Dans le champ widthSol entrez 750.
Dans le champ heightSol entrez 200.
Laissez 0 dans le champ nbLatexSol
Le champ infoParam sert à indiquer quels sont les paramètres qui peuvent être imposés par l'utilisateur.
Entrez dans ce champ de code suivant :
Cet exercice n'est pas paramétrable par l'utilisateur.
Vous pouvez maintenant valider la boîte de dialogue de choix des paramètres.
Ensuite cliquez en bas sur le bouton Enregistrer pour enregistrer votre ressource.
Si vous voulez maintenant tester votre ressource, fermez d’abord l’onglet Maîtriser la notion d'image et d'antécédent puis, dans Mes Ressources, faites un clic droit sur la ressource.
Vous pouvez maintenant tester la ressource.
Quelques compléments
Dans notre exemple, notre formulaire ne contenait au maximum qu'un éditeur de formule (repéré par edit1 dans le \text rendu par l'affichage LaTeX de tag formulaire) et qu'une liste de choix (repérée par list1 dans le \text rendu par l'affichage LaTeX de tag formulaire).
Il est tout à fait possible, dans un même formulaire, d'avoir plusieurs éditeurs de formule et plusieurs choix à liste déroulante.
Si, par exemple, vous utilisez deux listes déroulantes en insérant list1 et list2 dans le formulaire, vous devrez alors avoir deux affichages LaTeX de tags list1 et list2 qui renverront les items disponibles dans chacune des listes.
Si vous avez un deuxième éditeur de formule dans votre formulaire obtenu en insérant edit2 dans celui-ci, alors votre figure devra aussi contenir trois calculs nommés rep2, exact2 et resolu2.
rep2 contiendra la réponse de l'élève dans l'éditeur repéré par edit2 dans le formulaire (la formule que vous mettez dans rep2 ne sert donc pas) et exact2 doit renvoyer 1 si la valeur contenue dans rep2 est bonne (mais non nécessairement simplifiée) et 0, sinon alors que resolu2 doit renvoyer 1 si rep2 contient une des réponses finales attendues pour le champ d'édition n°2.
Il est même possible de créer une formulaire s'étendant sur plusieurs lignes dans le cas d'un formulaire dynamique.
Voici un exemple de code LaTeX d'un affichage LaTeX auquel vous devrez affecter le tag formulaire comme expliqué ci-dessus :
\begin{array}{l}
\text{Heure "exacte" suivant \Val{a}h\If{t1}{0}{}\Val{b} : edit1 h}
\\ \text{Nombre de minutes entre \Val{a}h\If{t1}{0}{}\Val{b} et \Val{a'}h : edit2 min}
\\ \text{Nombre d'heures entre \Val{a'}h et \Val{c}h : edit3 h}
\\ \text{Nombre de minutes entre \Val{c}h et \Val{c}h\If{t2}{0}{}\Val{d} : edit4}
\\ \text{Total de minutes : edit5 min}
\\ \text{Comme edit10 > 60 donc edit11 min = edit8 h edit9 min}
\\ \text{Durée totale : edit6 h edit7 min}
\end{array}
Cette affichage LaTeX est un array donc chaque ligne est formée d'un seul affichage de texte qui contient ce qui doit être affiché dans chacune des lignes de correction. Chacun de ces affichages de texte peut d'ailleurs contenir des formules LaTeX, il suffit pour cela de les entourer de caractères $.
Il y a aussi des possibilités supplémentaires sur les listes déroulantes.
Si vous désirez par exemple que les items de la liste déroulante list1 soient mélangés au hasard quand ils sont présentés à l'élève, il suffit que votre figure contienne un calcul nommé listaleat1 valant 1.
Si vous désirez que plusieurs items de la liste list1 puissent être acceptés comme bons, votre figure doit contenir un calcul nommé repList1 qui doit être initialisé à une autre valeur que -1 (1 par exemple). C'est dans repList1 que le modèle mettra l'index de l'item qu'a choisi l'élève comme réponse.
Votre figure doit alors contenir un autre calcul nommé exactList1 qui vaut 1 si la réponse qu'a choisie l'élève (que le modèle a mis dans repList1) est une des réponses acceptés comme exactes et 0 sinon.