Table des matières
Exercice de calcul vectoriel (2)
Notre but est créer dans LaboMep un exercice analogue à cet exercice.
Une figure étant donnée à l'élève on lui demande d'exprimer en vecteur donné en fonction de deux vecteurs nommés i et j.
Pour créer cette ressource vous devez utiliser la version JavaScript de MathGraph32, version 6.6.0 ou ultérieure, ou utiliser la version en ligne sur le site de MathGraph32.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé avec prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé avec prise en charge des nombres complexes.
La mise en place de cette ressource étant un peu compliquée, ik est conseillé d'avoir au préalable lu ce tutoriel
Etape 1 : Création de la figure MathGraph
Dans ce tutoriel nous allons fournir la figure ci-dessous en Base 64 et expliquer les grandes lignes de sa création sans expliquer tous les détails.
Voici donc ci-dessous le code Base 64 de cette figure :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcvb6#gEA#wEAAAAAAAAAAAPZAAACpQAAAQEAAAAAAAAAAAAAAS7#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAPQ1ZhcmlhYmxlQm9ybmVlAP####8AA2NvcgAAAAAAAAAAAAAAAAAAAAA#8AAAAAAAAD#wAAAAAAAAAAABMAABMQABMf####8AAAABAA9DQ2FsY3VsQ29tcGxleGUA#####wAFdmVjdDAAATAAAAABAAAAAAAAAAD#####AAAAAQAHQ0NhbGN1bAD#####AAVuYnZhcgABMQAAAAE#8AAAAAAAAAAAAAQA#####wAGbmJjYXMxAAIxMgAAAAFAKAAAAAAAAAAAAAQA#####wACcjEAE2ludChyYW5kKDApKm5iY2FzMSn#####AAAAAgAJQ0ZvbmN0aW9uAv####8AAAABAApDT3BlcmF0aW9uAgAAAAURAAAAAQAAAAAAAAAAP6SkcYhvBmD#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAABAAAAAQA#####wABZgAEMStyMQAAAAYAAAAAAT#wAAAAAAAAAAAABwAAAAUAAAAEAP####8AAmYxAANmPTEAAAAGCAAAAAcAAAAGAAAAAT#wAAAAAAAAAAAABAD#####AAJmMgADZj0yAAAABggAAAAHAAAABgAAAAFAAAAAAAAAAAAAAAQA#####wACZjMAA2Y9MwAAAAYIAAAABwAAAAYAAAABQAgAAAAAAAAAAAAEAP####8AAmY0AANmPTQAAAAGCAAAAAcAAAAGAAAAAUAQAAAAAAAAAAAABAD#####AAJmNQADZj01AAAABggAAAAHAAAABgAAAAFAFAAAAAAAAAAAAAQA#####wACZjYAA2Y9NgAAAAYIAAAABwAAAAYAAAABQBgAAAAAAAAAAAAEAP####8AAmY3AANmPTcAAAAGCAAAAAcAAAAGAAAAAUAcAAAAAAAAAAAABAD#####AAJmOAADZj04AAAABggAAAAHAAAABgAAAAFAIAAAAAAAAAAAAAQA#####wACZjkAA2Y9OQAAAAYIAAAABwAAAAYAAAABQCIAAAAAAAAAAAAEAP####8AA2YxMAAEZj0xMAAAAAYIAAAABwAAAAYAAAABQCQAAAAAAAAAAAAEAP####8AA2YxMQAEZj0xMQAAAAYIAAAABwAAAAYAAAABQCYAAAAAAAAAAAAEAP####8AA2YxMgAEZj0xMgAAAAYIAAAABwAAAAYAAAABQCgAAAAAAAD#####AAAAAgAGQ0xhdGV4AP####8BAAAAAQAA#####xBAc8AAAAAAAMAEzMzMzM0AAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAIbXElme2YxfQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtBRn19Cn0KewpcSWZ7ZjJ9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JEfX0KfQp7ClxJZntmM30Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17RkJ9fQp9CnsKXElme2Y0fQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtFQn19Cn0KewpcSWZ7ZjV9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0FFfX0KfQp7ClxJZntmNn0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0d9fQp9CnsKXElme2Y3fQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtJQX19Cn0KewpcSWZ7Zjh9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0dDfX0KfQp7ClxJZntmOX0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17REd9fQp9CnsKXElme2YxMH0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17SEV9fQp9CnsKXElme2YxMX0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17SUh9fQp9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JcLEl9fQp9Cn0KfQp9Cn0KfQp9Cn0KfQp9Cn3#####AAAAAQAKQ1BvaW50QmFzZQD#####AQAAAAAOAAJPJwDAKAAAAAAAAAAAAAAAAAAAAAAFAAFAT4AAAAAAAEB0NmZmZmZm#####wAAAAEAFENEcm9pdGVEaXJlY3Rpb25GaXhlAP####8BAAAAABAAAAEAAAABAAAAFAE#8AAAAAAAAP####8AAAABAA9DUG9pbnRMaWVEcm9pdGUA#####wEAAAAADgACSScAwBgAAAAAAAAAAAAAAAAAAAAABQABQEDvXCj1wo8AAAAV#####wAAAAEACUNEcm9pdGVBQgD#####AQAAAAAQAAABAAAAAQAAABQAAAAW#####wAAAAEAFkNEcm9pdGVQZXJwZW5kaWN1bGFpcmUA#####wEAAAAAEAAAAQAAAAEAAAAUAAAAF#####8AAAABAAlDQ2VyY2xlT0EA#####wEAAAAAAAABAAAAFAAAABb#####AAAAAQAQQ0ludERyb2l0ZUNlcmNsZQD#####AAAAGAAAABn#####AAAAAQAQQ1BvaW50TGllQmlwb2ludAD#####AQAAAAAQAAABAAAFAAEAAAAaAAAAEAD#####AQAAAAAOAAJKJwDAKAAAAAAAAMAQAAAAAAAAAAAFAAIAAAAa#####wAAAAIAB0NSZXBlcmUA#####wDm5uYAAAABAAAAFAAAABYAAAAcAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAA#####wAAAAEACkNVbml0ZXhSZXAA#####wAEdW5pdAAAAB3#####AAAAAQALQ0hvbW90aGV0aWUA#####wAAABQAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAAe#####wAAAAEAC0NQb2ludEltYWdlAP####8BAAAAABAAAlciAQAAAQAAAAAWAAAAH#####8AAAABAAlDTG9uZ3VldXIA#####wAAABQAAAAgAAAACQD#####AAAAAAAQAAFBAMAcAAAAAAAAQAgAAAAAAAAAAAUAAUBZwAAAAAAAQHFGZmZmZmYAAAAKAP####8BAAAAARAAAAEAAAABAAAAIgE#8AAAAAAAAAAAAAsA#####wAAAAAAEAABQgAAAAAAAAAAAEAIAAAAAAAAAAAFAAFAV8AAAAAAAAAAACMAAAAOAP####8BAAAAAAAAAQAAACIAAAAkAAAADgD#####AQAAAAAAAAEAAAAkAAAAIv####8AAAABABBDSW50Q2VyY2xlQ2VyY2xlAP####8AAAAlAAAAJgAAABAA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAQAAACcAAAAQAP####8AAAAAABAAAU8AwBgAAAAAAABAGAAAAAAAAAAABQACAAAAJ#####8AAAABAAlDUm90YXRpb24A#####wAAACkAAAAGAwAAAAcAAAAAAAAAAUAIAAAAAAAAAAAAFAD#####AAAAAAAOAAFDAEAgAAAAAAAAwCgAAAAAAAAAAAUAAAAAJAAAACoAAAAUAP####8AAAAAAA4AAUQAwBAAAAAAAADANwAAAAAAAAAABQAAAAArAAAAKgAAABQA#####wAAAAAADgABRQDAIAAAAAAAAMA1AAAAAAAAAAAFAAAAACwAAAAqAAAAFAD#####AAAAAAAOAAFGAMAzAAAAAAAAwCIAAAAAAAAAAAUAAAAALQAAACr#####AAAAAQAIQ1NlZ21lbnQA#####wAAAAAAEAAAAQAAAAEAAAAiAAAAJAAAABgA#####wAAAAAAEAAAAQAAAAEAAAAkAAAAKwAAABgA#####wAAAAAAEAAAAQAAAAEAAAArAAAALAAAABgA#####wAAAAAAEAAAAQAAAAEAAAAsAAAALQAAABgA#####wAAAAAAEAAAAQAAAAEAAAAtAAAALgAAABgA#####wAAAAAAEAAAAQAAAAEAAAAuAAAAIgAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAAIgAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAAJAAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAAKwAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAALAAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAALQAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAALv####8AAAABAA5DTWFycXVlU2VnbWVudAD#####AAAA#wAAAAIAAAAAMwAAABkA#####wAAAP8AAAACAAAAADQAAAAZAP####8AAAD#AAAAAgAAAAAvAAAAGQD#####AAAA#wAAAAIAAAAAMAAAABkA#####wAAAP8AAAACAAAAADEAAAAZAP####8AAAD#AAAAAgAAAAAyAAAAGQD#####AAAA#wAAAAIAAAAANQAAABkA#####wAAAP8AAAACAAAAADYAAAAZAP####8AAAD#AAAAAgAAAAA3AAAAGQD#####AAAA#wAAAAIAAAAAOAAAABkA#####wAAAP8AAAACAAAAADkAAAAZAP####8AAAD#AAAAAgAAAAA6#####wAAAAEAEUNTeW1ldHJpZUNlbnRyYWxlAP####8AAAArAAAAFAD#####AAAAAAAQAAFIAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALAAAAEcAAAAaAP####8AAAAuAAAAFAD#####AAAAAAAQAAFHAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALQAAAEkAAAAYAP####8AAAAAABAAAAEAAAABAAAALgAAAEoAAAAYAP####8AAAAAABAAAAEAAAABAAAASgAAACIAAAAYAP####8AAAAAABAAAAEAAAABAAAAJAAAAEgAAAAYAP####8AAAAAABAAAAEAAAABAAAASAAAACsAAAAaAP####8AAAAsAAAAFAD#####AAAAAAAQAAFJAMAIAAAAAAAAwDgAAAAAAAAAAAUAAAAAKwAAAE8AAAAYAP####8AAAAAABAAAAEAAAABAAAALQAAAFAAAAAYAP####8AAAAAABAAAAEAAAABAAAAUAAAACwAAAAZAP####8AAAD#AAAAAgAAAABLAAAAGQD#####AAAA#wAAAAIAAAAATAAAABkA#####wAAAP8AAAACAAAAAE0AAAAZAP####8AAAD#AAAAAgAAAABOAAAAGQD#####AAAA#wAAAAIAAAAAUgAAABkA#####wAAAP8AAAACAAAAAFH#####AAAAAQAIQ1ZlY3RldXIA#####wD#AAAAEAAAAQAAAAIAAAApAAAAKwD#####AAAAAQAHQ01pbGlldQD#####Af8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAApAAAAKwAAAAgA#####wD#AAAAQBwAAAAAAAA#8AAAAAAAAAAAAAAAWhQAAAAAAAEAAAAAAAAAAQAAAAAAAAAAAAdcdmVje2l9AAAAGwD#####AAB#AAAQAAABAAAAAgAAACkAAAAsAAAAABwA#####wEAfwAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAKQAAACwAAAAIAP####8AAH8AAMAiAAAAAAAAP#AAAAAAAAAAAAAAAF0UAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAHXHZlY3tqff####8AAAACAA1DTWVzdXJlQWZmaXhlAP####8AAU8AAAAdAAAAKQAAAB0A#####wABQQAAAB0AAAAiAAAAHQD#####AAFCAAAAHQAAACQAAAAdAP####8AAUMAAAAdAAAAKwAAAB0A#####wABRAAAAB0AAAAsAAAAHQD#####AAFFAAAAHQAAAC0AAAAdAP####8AAUYAAAAdAAAALgAAAB0A#####wABRwAAAB0AAABKAAAAHQD#####AAFIAAAAHQAAAEgAAAAdAP####8AAUkAAAAdAAAAUAAAAAMA#####wACaScAA0MtTwAAAAYB#####wAAAAEAF0NSZXN1bHRhdFZhbGV1ckNvbXBsZXhlAAAAYgAAAB4AAABfAAAAAwD#####AAFqAANELU8AAAAGAQAAAB4AAABjAAAAHgAAAF8AAAADAP####8AA3JlcAABMAAAAAEAAAAAAAAAAAAAAAMA#####wAEc29sMQAFLWknK2oAAAAGAP####8AAAABAAxDTW9pbnNVbmFpcmUAAAAeAAAAaQAAAB4AAABqAAAAAwD#####AARzb2wyAActaScrMipqAAAABgAAAAAfAAAAHgAAAGkAAAAGAgAAAAFAAAAAAAAAAAAAAB4AAABqAAAAAwD#####AARzb2wzAAYyKmknLWoAAAAGAQAAAAYCAAAAAUAAAAAAAAAAAAAAHgAAAGkAAAAeAAAAagAAAAMA#####wAEc29sNAAIMippJy0yKmoAAAAGAQAAAAYCAAAAAUAAAAAAAAAAAAAAHgAAAGkAAAAGAgAAAAFAAAAAAAAAAAAAAB4AAABqAAAAAwD#####AARzb2w1AActaScrMipqAAAABgAAAAAfAAAAHgAAAGkAAAAGAgAAAAFAAAAAAAAAAAAAAB4AAABqAAAAAwD#####AARzb2w2AAUtaSctagAAAAYBAAAAHwAAAB4AAABpAAAAHgAAAGoAAAADAP####8ABHNvbDcABmknLTMqagAAAAYBAAAAHgAAAGkAAAAGAgAAAAFACAAAAAAAAAAAAB4AAABqAAAAAwD#####AARzb2w4AAYyKmknK2oAAAAGAAAAAAYCAAAAAUAAAAAAAAAAAAAAHgAAAGkAAAAeAAAAagAAAAMA#####wAEc29sOQAHLWknLTIqagAAAAYBAAAAHwAAAB4AAABpAAAABgIAAAABQAAAAAAAAAAAAAAeAAAAagAAAAMA#####wAFc29sMTAACS0zKmknKzIqagAAAAYAAAAAHwAAAAYCAAAAAUAIAAAAAAAAAAAAHgAAAGkAAAAGAgAAAAFAAAAAAAAAAAAAAB4AAABqAAAAAwD#####AAVzb2wxMQAIMyppJy0zKmoAAAAGAQAAAAYCAAAAAUAIAAAAAAAAAAAAHgAAAGkAAAAGAgAAAAFACAAAAAAAAAAAAB4AAABqAAAAAwD#####AAVzb2wxMgAJLTIqaScrMypqAAAABgAAAAAfAAAABgIAAAABQAAAAAAAAAAAAAAeAAAAaQAAAAYCAAAAAUAIAAAAAAAAAAAAHgAAAGr#####AAAAAwAQQ1Rlc3RFcXVpdmFsZW5jZQD#####AAR0ZXExAAAAbAAAAGsBAQAAAAE#8AAAAAAAAAEAAAAgAP####8ABHRlcTIAAABtAAAAawEBAAAAAT#wAAAAAAAAAQAAACAA#####wAEdGVxMwAAAG4AAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAR0ZXE0AAAAbwAAAGsBAQAAAAE#8AAAAAAAAAEAAAAgAP####8ABHRlcTUAAABwAAAAawEBAAAAAT#wAAAAAAAAAQAAACAA#####wAEdGVxNgAAAHEAAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAR0ZXE3AAAAcgAAAGsBAQAAAAE#8AAAAAAAAAEAAAAgAP####8ABHRlcTgAAABzAAAAawEBAAAAAT#wAAAAAAAAAQAAACAA#####wAEdGVxOQAAAHQAAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAV0ZXExMAAAAHUAAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAV0ZXExMQAAAHYAAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAV0ZXExMgAAAHcAAABrAQEAAAABP#AAAAAAAAABAAAABAD#####AAZyZXNvbHUAjXNpKGYxLHRlcTEsc2koZjIsdGVxMixzaShmMyx0ZXEzLHNpKGY0LHRlcTQsc2koZjUsdGVxNSxzaShmNix0ZXE2LHNpKGY3LHRlcTcsc2koZjgsdGVxOCxzaShmOSx0ZXE5LHNpKGYxMCx0ZXExMCxzaShmMTEsdGVxMTEsdGVxMTIpKSkpKSkpKSkpKf####8AAAABAA1DRm9uY3Rpb24zVmFyAAAAAAcAAAAHAAAABwAAAHgAAAAhAAAAAAcAAAAIAAAABwAAAHkAAAAhAAAAAAcAAAAJAAAABwAAAHoAAAAhAAAAAAcAAAAKAAAABwAAAHsAAAAhAAAAAAcAAAALAAAABwAAAHwAAAAhAAAAAAcAAAAMAAAABwAAAH0AAAAhAAAAAAcAAAANAAAABwAAAH4AAAAhAAAAAAcAAAAOAAAABwAAAH8AAAAhAAAAAAcAAAAPAAAABwAAAIAAAAAhAAAAAAcAAAAQAAAABwAAAIEAAAAhAAAAAAcAAAARAAAABwAAAIIAAAAHAAAAg#####8AAAABAA1DRm9uY0NvbXBsZXhlAP####8ABHplcm8AEmFicyh6KTwwLjAwMDAwMDAwMQAAAAYEAAAABUD#####AAAAAgARQ1ZhcmlhYmxlRm9ybWVsbGUAAAAAAAAAAT4RLgvoJtaVAAF6AAAAAwD#####AAV0ZXN0MQAOemVybyhyZXAtc29sMSn#####AAAAAQAWQ0FwcGVsRm9uY3Rpb25Db21wbGV4ZQAAAIUAAAAGAQAAAB4AAABrAAAAHgAAAGwAAAADAP####8ABXRlc3QyAA56ZXJvKHJlcC1zb2wyKQAAACQAAACFAAAABgEAAAAeAAAAawAAAB4AAABtAAAAAwD#####AAV0ZXN0MwAOemVybyhyZXAtc29sMykAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAbgAAAAMA#####wAFdGVzdDQADnplcm8ocmVwLXNvbDQpAAAAJAAAAIUAAAAGAQAAAB4AAABrAAAAHgAAAG8AAAADAP####8ABXRlc3Q1AA56ZXJvKHJlcC1zb2w1KQAAACQAAACFAAAABgEAAAAeAAAAawAAAB4AAABwAAAAAwD#####AAV0ZXN0NgAOemVybyhyZXAtc29sNikAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAcQAAAAMA#####wAFdGVzdDcADnplcm8ocmVwLXNvbDcpAAAAJAAAAIUAAAAGAQAAAB4AAABrAAAAHgAAAHIAAAADAP####8ABXRlc3Q4AA56ZXJvKHJlcC1zb2w4KQAAACQAAACFAAAABgEAAAAeAAAAawAAAB4AAABzAAAAAwD#####AAV0ZXN0OQAOemVybyhyZXAtc29sOSkAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAdAAAAAMA#####wAGdGVzdDEwAA96ZXJvKHJlcC1zb2wxMCkAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAdQAAAAMA#####wAGdGVzdDExAA96ZXJvKHJlcC1zb2wxMSkAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAdgAAAAMA#####wAGdGVzdDEyAA96ZXJvKHJlcC1zb2wxMikAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAd#####8AAAABAA1DUGFydGllUmVlbGxlAP####8ABmV4YWN0MQAAAIYAAAAlAP####8ABmV4YWN0MgAAAIcAAAAlAP####8ABmV4YWN0MwAAAIgAAAAlAP####8ABmV4YWN0NAAAAIkAAAAlAP####8ABmV4YWN0NQAAAIoAAAAlAP####8ABmV4YWN0NgAAAIsAAAAlAP####8ABmV4YWN0NwAAAIwAAAAlAP####8ABmV4YWN0OAAAAI0AAAAlAP####8ABmV4YWN0OQAAAI4AAAAlAP####8AB2V4YWN0MTAAAACPAAAAJQD#####AAdleGFjdDExAAAAkAAAACUA#####wAHZXhhY3QxMgAAAJEAAAAEAP####8ABWV4YWN0AKVzaShmMSxleGFjdDEsc2koZjIsZXhhY3QyLHNpKGYzLGV4YWN0MyxzaShmNCxleGFjdDQsc2koZjUsZXhhY3Q1LHNpKGY2LGV4YWN0NixzaShmNyxleGFjdDcsc2koZjgsZXhhY3Q4LHNpKGY5LGV4YWN0OSxzaShmMTAsZXhhY3QxMCxzaShmMTEsZXhhY3QxMSxleGFjdDEyKSkpKSkpKSkpKSkAAAAhAAAAAAcAAAAHAAAABwAAAJIAAAAhAAAAAAcAAAAIAAAABwAAAJMAAAAhAAAAAAcAAAAJAAAABwAAAJQAAAAhAAAAAAcAAAAKAAAABwAAAJUAAAAhAAAAAAcAAAALAAAABwAAAJYAAAAhAAAAAAcAAAAMAAAABwAAAJcAAAAhAAAAAAcAAAANAAAABwAAAJgAAAAhAAAAAAcAAAAOAAAABwAAAJkAAAAhAAAAAAcAAAAPAAAABwAAAJoAAAAhAAAAAAcAAAAQAAAABwAAAJsAAAAhAAAAAAcAAAARAAAABwAAAJwAAAAHAAAAnQAAAAQA#####wAHcmVwb25zZQAac2kocmVzb2x1LDEsc2koZXhhY3QsMiwwKSkAAAAhAAAAAAcAAACEAAAAAT#wAAAAAAAAAAAAIQAAAAAHAAAAngAAAAFAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAgA#####wEAAAABAAVwb2ludP####8QQHPgAAAAAABAcEZmZmZmZgAAAAAAAAAAAAAAAAABAAAAAAAAAAAAI1x0ZXh0e08vL0EvL0IvL0MvL0QvL0UvL0YvL0cvL0gvL0l9AAAACAD#####AQAAAAEABHZlY3T#####EEB0EAAAAAAAQHHmZmZmZmYAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAtcdGV4dHtpLy9qfQAAAAgA#####wEAAP8BAAD#####EkBz8AAAAAAAQEUzMzMzMzMBAe#v+wAAAAAAAAAAAAAAAQAAAAAAAAAACuJcYmVnaW57YXJyYXl9e2x9ClxJZntmMX0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QUZ9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QUd9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17R0Z9fT0tXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QUZ9fT0tXHZlY3tpfStcdmVje2p9Cn0KewpcSWZ7ZjJ9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JEfX09XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JBfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0FEfX09LVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPQ319K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPRH19ClxcXHRleHR7ZG9uYyB9XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JEfX09LVx2ZWN7aX0rMlx2ZWN7an0KfQp7ClxJZntmM30Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17RkJ9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17Rkd9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17R0J9fT0tXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0rMlxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPQ319ClxcXHRleHR7ZG9uYyB9XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0ZCfX09Mlx2ZWN7aX0tXHZlY3tqfQp9CnsKXElme2Y0fQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtFQn19PVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtFR319K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHQn19PS0yXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0rMlxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPQ319ClxcXHRleHR7ZG9uYyB9XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0VCfX09Mlx2ZWN7aX0tMlx2ZWN7an0KfQp7ClxJZntmNX0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QUV9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QUd9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17R0V9fT0tXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0rMlxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPRH19ClxcXHRleHR7ZG9uYyB9XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0VCfX09LVx2ZWN7aX0rMlx2ZWN7an0KfQp7ClxJZntmNn0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0d9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0F9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QUd9fT0tXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0tXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0d9fT0tXHZlY3tpfS1cdmVje2p9Cn0KewpcSWZ7Zjd9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0lBfX09XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0lHfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0dBfX09LTNcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0N9fQpcXFx0ZXh0e2RvbmMgfVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPR319PVx2ZWN7aX0tM1x2ZWN7an0KfQp7ClxJZntmOH0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17R0N9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17R0J9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QkN9fT0yXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17R0N9fT0yXHZlY3tpfStcdmVje2p9Cn0KewpcSWZ7Zjl9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0RHfX09XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0RFfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0VHfX09LVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPQ319LTJcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fQpcXFx0ZXh0e2RvbmMgfVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPR319PS1cdmVje2l9LTJcdmVje2p9Cn0KewpcSWZ7ZjEwfQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtIRX19PVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtIR319K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHRX19PS0zXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0rMlxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPRH19ClxcXHRleHR7ZG9uYyB9XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0hFfX09LTNcdmVje2l9KzJcdmVje2p9Cn0KewpcSWZ7ZjExfQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtJSH19PVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtJR319K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHSH19PS0zXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0rM1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPQ319ClxcXHRleHR7ZG9uYyB9XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0lIfX09M1x2ZWN7aX0tM1x2ZWN7an0KfQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtCXCxJfX09XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JHfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0dJfX09LTJcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fSszXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QlwsSX19PS0yXHZlY3tpfSszXHZlY3tqfQp9IAp9IAp9IAp9IAp9IAp9IAp9IAp9IAp9IAp9IAp9IApcZW5ke2FycmF5fQAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAAIAAAAFAD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAkAAAAowAAABsA#####wD#AP8AEAAAAQAAAAIAAACkAAAALAAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAHAAAACQAAABQA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALgAAAKYAAAAbAP####8A#wD#ABAAAAEAAAACAAAApwAAACQAAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAAAoAAAAUAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAC0AAACpAAAAGwD#####AP8A#wAQAAABAAAAAgAAAKoAAAAkAAAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAALAAAAFAD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAtAAAArAAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAAMAAAAFAD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABKAAAArgAAABsA#####wD#AP8AEAAAAQAAAAIAAAApAAAArwAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAHAAAADQAAABQA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAUAAAALEAAAAbAP####8A#wD#ABAAAAEAAAACAAAAsgAAACIAAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAAA4AAAAUAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEoAAAC0AAAAGwD#####AP8A#wAQAAABAAAAAgAAALUAAAArAAAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAAPAAAAFAD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAsAAAAtwAAABsA#####wD#AP8AEAAAAQAAAAIAAAC4AAAASgAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAHAAAAEAAAABQA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAASAAAALoAAAAbAP####8A#wD#ABAAAAEAAAACAAAAuwAAAC0AAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAABEAAAAUAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEgAAAC9AAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAABIAAAAUAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACQAAAC#AAAAGwD#####AP8A#wAQAAABAAAAAgAAAMAAAABQAAAAABsA#####wD#AP8AEAAAAQAAAAIAAAAiAAAArQAAAAAbAP####8A#wD#ABAAAAEAAAACAAAAUAAAAL4AAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAAAcAAAAUAP####8A#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACIAAADEAAAAGwD#####AP8A#wAQAAABAAAAAgAAAMUAAAAuAAAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAYKAAAABwAAAAEAAAAHAAAABwAAABQA#####wB#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAASgAAAMcAAAAbAP####8AfwAAABAAAAEAAAACAAAAxQAAAMgAAAAAGwD#####AAB#fwAQAAABAAAAAgAAAMgAAAAuAAAAABwA#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAxQAAAMgAAAAIAP####8AfwAAAQAAAAAAyxIAAAAAAAEAAAAAAAAAAQAAAAAAAAAAAAgtXHZlY3tpfQAAABwA#####wAAf38AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAyAAAAC4AAAAIAP####8AAH9#AMAgAAAAAAAAQAgAAAAAAAAAAAAAAM0SAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAHXHZlY3tqfQAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAYKAAAABwAAAAEAAAAHAAAACAAAABQA#####wB#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAIgAAAM8AAAAcAP####8AfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACQAAADQAAAACAD#####AH8AAAEAAAAAANESAAAAAAABAAAAAAAAAAEAAAAAAAAAAAAILVx2ZWN7aX0AAAANAP####8BAH8AABAAAAEAAAACAAAA0AAAADUAAAALAP####8BAH8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAE#sQ7a0wIluwAAANP#####AAAAAQAMQ1RyYW5zbGF0aW9uAP####8AAADQAAAALAAAABQA#####wEAfwAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAA1AAAANUAAAAbAP####8AAP8AABAAAAEAAAACAAAA1AAAANYAAAAAHAD#####AAD##wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAADUAAAA1gAAAAgA#####wAA#wAAwBgAAAAAAAA#8AAAAAAAAAAAAAAA2BAAAAAAAAIAAAACAAAAAQAAAAAAAAAAAAgyXHZlY3tqfQAAABsA#####wB#AAAAEAAAAQAAAAIAAAAkAAAA0AAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAAkAAAAUAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEoAAADbAAAAHAD#####AQB#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAuAAAA3AAAABsA#####wAA#wAAEAAAAQAAAAIAAAAuAAAA3AAAAAAIAP####8AAP8AAMAUAAAAAAAAwBAAAAAAAAAAAAAAAN0QAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAILVx2ZWN7an0AAAAbAP####8AfwAAABAAAAEAAAACAAAA3AAAACQAAAAAHAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAADcAAAAJAAAAAgA#####wB#AAAAQCQAAAAAAADAGAAAAAAAAAAAAAAA4RIAAfb6#gAAAAEAAAACAAAAAQAAAAAAAAAAAAgyXHZlY3tpfQAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAYKAAAABwAAAAEAAAAHAAAACgAAABQA#####wF#AH8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAASgAAAOMAAAAcAP####8BfwB#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACQAAADkAAAACAD#####AH8AfwBAMwAAAAAAAL#wAAAAAAAAAAAAAADlEgAAAAAAAQAAAAAAAAABAAAAAAAAAAAACDJcdmVje2l9AAAAGwD#####AH8AfwAQAAABAAAAAgAAAOQAAAAkAAAAABwA#####wEA#wAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALQAAAOQAAAAbAP####8AAP8AABAAAAEAAAACAAAALQAAAOQAAAAACAD#####AAD#AABAAAAAAAAAAMAQAAAAAAAAAAAAAADoEgAAAAAAAgAAAAIAAAABAAAAAAAAAAAACS0yXHZlY3tqfQAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAYKAAAABwAAAAEAAAAHAAAACwAAABQA#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAASgAAAOsAAAAcAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACIAAADsAAAAGwD#####AH8AAAAQAAABAAAAAgAAACIAAADsAAAAAAgA#####wB#AAABAAAAAADtEgAAAAAAAQAAAAAAAAABAAAAAAAAAAAACC1cdmVje2l9AAAAHAD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAADsAAAALQAAABsA#####wAA#wAAEAAAAQAAAAIAAADsAAAALQAAAAAIAP####8AAP8AAL#wAAAAAAAAwBgAAAAAAAAAAAAAAPAQAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAIMlx2ZWN7an0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAAwAAAAUAP####8BAP8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACIAAADzAAAAHAD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAApAAAA9AAAABsA#####wAA#wAAEAAAAQAAAAIAAAApAAAA9AAAAAAIAP####8AAP8AAQAAAAAA9RIAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAgtXHZlY3tqfQAAABwA#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAA9AAAAEoAAAAbAP####8AfwAAABAAAAEAAAACAAAA9AAAAEoAAAAACAD#####AH8AAAEAAAAAAPgSAAAAAAABAAAAAAAAAAEAAAAAAAAAAAAILVx2ZWN7aX0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAA0AAAAUAP####8BAP8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEoAAAD7AAAAHAD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABQAAAA#AAAABsA#####wAA#wAAEAAAAQAAAAIAAABQAAAA#AAAAAAIAP####8AAP8AAMAAAAAAAAAAwBAAAAAAAAAAAAAAAP0SAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAJLTNcdmVje2p9AAAAHAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAD8AAAAIgAAABsA#####wB#AAAAEAAAAQAAAAIAAAD8AAAAIgAAAAAIAP####8AfwAAAMAIAAAAAAAAQAgAAAAAAAAAAAAAAQASAAAAAAABAAAAAAAAAAEAAAAAAAAAAAAHXHZlY3tpfQAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAYKAAAABwAAAAEAAAAHAAAADgAAABQA#####wB#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAJAAAAQMAAAAcAP####8AfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEoAAAEEAAAAGwD#####AH8AAAAQAAABAAAAAgAAAEoAAAEEAAAAAAgA#####wB#AAAAQBgAAAAAAAAAAAAAAAAAAAAAAAABBRIAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAgyXHZlY3tpfQAAABwA#####wAAfwAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAABBAAAACsAAAAbAP####8AAH8AABAAAAEAAAACAAABBAAAACsAAAAACAD#####AAB#AABAFAAAAAAAAMAIAAAAAAAAAAAAAAEIEAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAB1x2ZWN7an0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAA8AAAAUAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAC0AAAELAAAAHAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAsAAABDAAAABsA#####wB#AAAAEAAAAQAAAAIAAAAsAAABDAAAAAAIAP####8AfwAAAMAQAAAAAAAAwBAAAAAAAAAAAAAAAQ0SAAAAAAABAAAAAgAAAAEAAAAAAAAAAAAILVx2ZWN7aX0AAAAcAP####8BAP8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAQwAAABKAAAAGwD#####AAD#AAAQAAABAAAAAgAAAQwAAABKAAAAAAgA#####wAA#wAAAAAAAAAAAADAGAAAAAAAAAAAAAABEBIAAAAAAAIAAAACAAAAAQAAAAAAAAAAAAktMlx2ZWN7an0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAABAAAAAUAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEoAAAETAAAAHAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABIAAABFAAAABsA#####wB#AAAAEAAAAQAAAAIAAABIAAABFAAAAAAIAP####8AfwAAAAAAAAAAAAAAP#AAAAAAAAAAAAAAARUQAAAAAAABAAAAAAAAAAEAAAAAAAAAAAAJLTNcdmVje2l9AAAAHAD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAEUAAAALQAAAAgA#####wAA#wAAwAAAAAAAAADAGAAAAAAAAAAAAAABGBIAAAAAAAIAAAACAAAAAQAAAAAAAAAAAAgyXHZlY3tqfQAAABsA#####wAA#wAAEAAAAQAAAAIAAAEUAAAALQAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAABEAAAAUAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEoAAAEbAAAAHAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAEcAAAASAAAAAgA#####wB#AAAAv#AAAAAAAABAAAAAAAAAAAAAAAABHRIAAAAAAAEAAAAAAAAAAQAAAAAAAAAAAAgzXHZlY3tpfQAAABsA#####wB#AAAAEAAAAQAAAAIAAAEcAAAASAAAAAAcAP####8BAP8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFAAAAEcAAAAGwD#####AAD#AAAQAAABAAAAAgAAAFAAAAEcAAAAAAgA#####wAA#wAAwBQAAAAAAADACAAAAAAAAAAAAAABIBIAAAAAAAIAAAACAAAAAQAAAAAAAAAAAAktM1x2ZWN7an0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAABIAAAAUAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEoAAAEjAAAAHAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAkAAABJAAAABsA#####wB#AAAAEAAAAQAAAAIAAAAkAAABJAAAAAAIAP####8AfwAAAMBFgAAAAAAAwAAAAAAAAAAAAAAAASUSAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAJLTNcdmVje2l9AAAAHAD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAEkAAAAUAAAABsA#####wAA#wAAEAAAAQAAAAIAAAEkAAAAUAAAAAAIAP####8AAP8AAMAIAAAAAAAAwAgAAAAAAAAAAAAAASgSAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAIM1x2ZWN7an3#####AAAAAQAQQ01hY3JvQXBwYXJpdGlvbgD#####AQAA#wEAAP####8QQHPwAAAAAABAZUzMzMzMzQIB9vr+AAAAAAAAAAAAAAABAAAAAAAAAAAADXZvaXIgc29sdXRpb24AAAAAAAEAAACiAP####8AAAABAB9DTWFjcm9BZmZlY3RhdGlvblZhbGV1clZhcmlhYmxlAP####8BAAD#AQAA#####xBAc#AAAAAAAEBrTMzMzMzNAgH2+v4AAAAAAAAAAAAAAAEAAAAAAAAAAAAHY29yID0gMQAAAAAAAT#wAAAAAAAAAAAAAf####8AAAABABFDTWFjcm9TdWl0ZU1hY3JvcwD#####AQAA#wEAAP####8QQHyQAAAAAABAZWzMzMzMzQIB9vr+AAAAAAAAAAAAAAABAAAAAAAAAAAACHNvbHV0aW9uAAAAAAACAAABLAAAASsAAAAh##########8=
Pour l'ouvrir dans MathGraph32, utilisez l'icône ![]() de création d'une figure et choisissez Figure par code Base 64 et, dans la boîte de dialogue qui s'ouvre, collez le code Base 64 ci-dessus.
de création d'une figure et choisissez Figure par code Base 64 et, dans la boîte de dialogue qui s'ouvre, collez le code Base 64 ci-dessus.
A part la figure elle-même, certains éléments nt été cachés ou ne sont pas visibles.
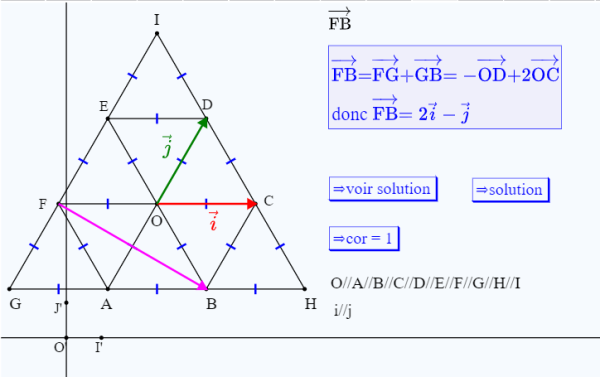
Voici ci-dessous un aperçu de la figure dans laquelle certains éléments ont été démasqués :
Pour créer les éléments géométriques de base de cette figure, on a d'abord utilisé l'icône ![]() puis choisi de créer une figure munie d'un repère en décochant les cases Quadrillage vertical et Quadrillage horizontal et en sélectionnant la case Sans graduation.
puis choisi de créer une figure munie d'un repère en décochant les cases Quadrillage vertical et Quadrillage horizontal et en sélectionnant la case Sans graduation.
Les points O, I et J définissant le repère ont ensuite été renommés en O', I' et J' puis avec l'outil on a masqué le point O', le point I', le point J' et les droites (O'I') et (O'J').
Le point A a ensuite été créé comme un point libre. Nous ne détaillerons pas la façon de créer les points B, C, D, E, F, G, H, I et O assez classique. La figure a ensuite été enrichie de segments et de marques de segments (que l'on crée avec l'outil ![]() et en cliquant sur le segment après avoir choisi une épaisseur de trait et une couleur).
et en cliquant sur le segment après avoir choisi une épaisseur de trait et une couleur).
Vous pouvez maintenant examiner comment a été créée cette figure en utilisant dans la barre supérieure l'outil ![]() protocole. En utilisant les touches haut et bas vous pouvez naviguer dans la figure pour voir les différents éléments de celle-ci.
protocole. En utilisant les touches haut et bas vous pouvez naviguer dans la figure pour voir les différents éléments de celle-ci.
Nous détaillerons ci-dessous les éléments de cette figure, à l'exception de ceux qui ont servi à la création de des éléments géométriques de base. Le calcul pi fait partie de toutes les figures et n'est pas modifiable (il ne s'agit bien sûr que d'une valeur approchée).
Suivent ensuite 12 calculs réels f1 à f12 qui servent plus tard dans les affichages LaTeX conditionnels.
Par exemple, le calcul f1 est défini par la formule f = 1 et prend comme valeur 1 si f est égal à 1 et 0 sinon.
Ensuite arrivent dans le protocole un affichage LaTeX libre indiqué dans le protocole par lat1: Affichage LaTeX
Cet affichage LaTeX a été crée avec l'outil ![]() et est récupéré par la ressource pour compléter la consigne (voir plus loin dans la paramétrage de la ressource).
et est récupéré par la ressource pour compléter la consigne (voir plus loin dans la paramétrage de la ressource).
Il est important que cet affichage LaTeX soit le premier affichage LaTeX de la figure. Si ce n'était pas le cas il faudrait le reclasser.
Voici le code LaTeX de cet affichage qui utilise des affichages LaTeX conditionnels :
\If{f1}
{
\overrightarrow {\mathrm{AF}}
}
{
\If{f2}
{
\overrightarrow {\mathrm{BD}}
}
{
\If{f3}
{
\overrightarrow {\mathrm{FB}}
}
{
\If{f4}
{
\overrightarrow {\mathrm{EB}}
}
{
\If{f5}
{
\overrightarrow {\mathrm{AE}}
}
{
\If{f6}
{
\overrightarrow {\mathrm{OG}}
}
{
\If{f7}
{
\overrightarrow {\mathrm{IA}}
}
{
\If{f8}
{
\overrightarrow {\mathrm{GC}}
}
{
\If{f9}
{
\overrightarrow {\mathrm{DG}}
}
{
\If{f10}
{
\overrightarrow {\mathrm{HE}}
}
{
\If{f11}
{
\overrightarrow {\mathrm{IH}}
}
{
\overrightarrow {\mathrm{B\,I}}
}
}
}
}
}
}
}
}
}
}
}
Ainsi si, par exemple, f est égal à 1, le code LaTeX renvoyé sera : \overrightarrow {\mathrm{AF}}.
Dans la consigne, les caractères $£a£ seront alors remplacés par ce code LaTeX.
Détaillons la nature et l'objet de certains des éléments suivants de la igure visibles dans le protocole.
Ont ensuite été créés 10 mesures d'affixes des points O, A, B, C, D, E, F, G, H, I des points ayant les mêmes noms.
Pour créer par exemple la première on a utilisé l'outil ![]() situé dans la barre d'outils de créations de calculs, on a ensuite cliqué sur le point O. Une boîte de dialogue s'est ouverte. Le seul repère de la figure étant sélectionné par défaut, il suffit ensuite d'entre le nom de la mesure, ici O, et de valider la boîte de dialogue.
situé dans la barre d'outils de créations de calculs, on a ensuite cliqué sur le point O. Une boîte de dialogue s'est ouverte. Le seul repère de la figure étant sélectionné par défaut, il suffit ensuite d'entre le nom de la mesure, ici O, et de valider la boîte de dialogue.
Cas mesures complexes nous serviront pas la suite à valider la réponse de l'élève.
Ensuite ont été crées les calculs complexes suivants avec l'outil ![]() de création d'un calcul complexe.
de création d'un calcul complexe.
| Nom du calcul complexe | Formule | Commentaire |
|---|---|---|
| i' | C-O | Les résultats finaux de l'élève devront être exprimés en fonction de i' et de j. A noter que ce calcul est nommé i' mais que dans sa réponse l'élève utilisera la lettre i pour le vecteur correspondant |
| j | D-O | |
| rep | 0 | Ce calcul contiendra la réponse entrée par l'élève |
| sol1 | -i'+j | Contient la réponse finale attendue de l'élève si f = 1 |
| sol2 | -i'+2*j | Contient la réponse finale attendue de l'élève si f = 2 |
| sol3 | 2*i'-j | Contient la réponse finale attendue de l'élève si f = 3 |
| sol4 | 2*i'-2*j | Contient la réponse finale attendue de l'élève si f = 4 |
| sol5 | -i'+2*j | Contient la réponse finale attendue de l'élève si f = 5 |
| sol6 | -i'-j | Contient la réponse finale attendue de l'élève si f = 6 |
| sol7 | i'-3*j | Contient la réponse finale attendue de l'élève si f = 7 |
| sol8 | 2*i'+j | Contient la réponse finale attendue de l'élève si f = 8 |
| sol9 | -i'-2*j | Contient la réponse finale attendue de l'élève si f = 9 |
| sol10 | -3*i'+2*j | Contient la réponse finale attendue de l'élève si f = 10 |
| sol11 | 3*i'-3*j | Contient la réponse finale attendue de l'élève si f = 11 |
| sol12 | -2*i'+3*j | Contient la réponse finale attendue de l'élève si f = 12 |
Ensuite ont été créés 12 tests d'équivalences entre les calculs précédents et le calcul complexe rep. Ces tests ont pour nom teq1, teq2, …, teq12.
Pour cela il faut utiliser l'icône ![]() situé à droite de la barre de création de calculs quand elle est déroulée et choisir dans la liste Test d'équivalence.
situé à droite de la barre de création de calculs quand elle est déroulée et choisir dans la liste Test d'équivalence.
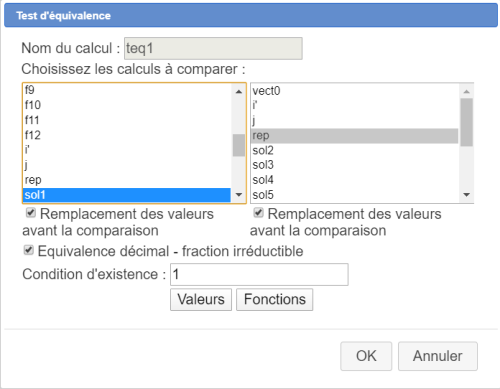
Voici par exemple comment a été crée le test d'équivalence nommé teq1 :
A noter qu'il faut cocher la case Remplacement des valeurs avant la comparaison à gauche et à droite. (Ainsi les valeurs des complexes A, B, C, D, E, F, G, H, I, O, i' et j seront remplacées avant de regarder si la réponse de l'élève contenue dans rep et le calcul solution sol1 sont des calculs équivalents.
Ensuite ont été créés les calculs ou fonctions suivants :
| Nom de l'objet | Nature | Formule | Commentaire |
|---|---|---|---|
| resolu | Calcul réel | si(f1,teq1,si(f2,teq2,si(f3,teq3,si(f4,teq4, si(f5,teq5,si(f6,teq6,si(f7,teq7,si(f8,teq8,si(f9,teq9, si(f10,teq10,si(f11,teq11,teq12))))))))))) | Renvoie 1 si la réponse de l'élève est équivalente à la réponse finale attendue et 0 sinon |
| zero | Fonction complexe de la variable z | abs(z)<0.000000001 | Renvoie le complexe 1 si le module de z est inférieur à 0.000000001 et 0 sinon |
| test1 | Calcul complexe | zero(rep-sol1) | Renvoie le complexe 1 si le module de la différence entre rep et sol1 est inférieur à 0.000000001 |
| … | |||
| test12 | Calcul complexe | zero(rep-sol12) | Renvoie le complexe 1 si le module de la différence entre rep et sol3 est inférieur à 0.000000001 |
Ensuite ont été créées 12 parties réelles de complexes nommées exact1 à exact12.
Pour créer une partie réelle de complexe, il faut utiliser l'icône ![]() situé à droite de la barre de création de calculs quand elle est déroulée et choisir dans la liste Partie réelle.
situé à droite de la barre de création de calculs quand elle est déroulée et choisir dans la liste Partie réelle.
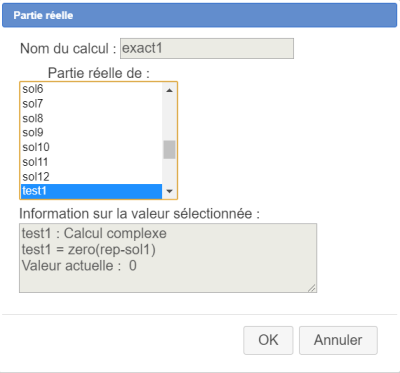
Voici par exemple la boîte de dialogue pour la création de exact1 :
Ensuite ont été créé les deux calculs réels suivants. Ce sont ces calculs qui vont indiquer sir la réponse de l'élève est bonne ou non, est bien la réponse finale attendue ou non.
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| exact | si(f1,exact1,si(f2,exact2,si(f3,exact3,si(f4,exact4, si(f5,exact5,si(f6,exact6,si(f7,exact7,si(f8,exact8, si(f9,exact9,si(f10,exact10,si(f11,exact11,exact12))))))))))) | Vaut 1 si la réponse de l'élève est exacte (à epsilon près |
| reponse | si(resolu,1,si(exact,2,0)) | C'est ce calcul valide la réponse de l'élève. Ce calcul renvoie 1 si la réponse de l'élève contenue dans rep est la réponse finale attendue, 2 si la réponse n'est pas finale mais est exacte et 0 sinon |
Ensuite ont été créés deux affichages LaTeX libres (lat4 et lat5 dans le protocole).
Le rôle du premier affichage LaTeX (lat4) est d'indiquer quels sont les noms des points que l'élève a le droit d'utiliser dans sa réponse.
Voici son code laTeX :
\text{O//A//B//C//D//E//F//G//H//I}
Le contenu du \text{} est le nom des points autorisés séparés les uns des autres par des doubles slash. Cet affichage LaTeX doit avoir pour tag point. Pour affecter ce tag à cet affichage LaTeX, on utilise l'outil protocole, on sélectionne l'affichage LaTeX et on clique sur le bouton Changer le tag.
Le rôle du second affichage LaTeX (lat5) est d'indiquer quels sont les noms des vecteurs que l'élève a le droit d'utiliser dans sa réponse.
Voici son code laTeX :
\text{i//j}
Le contenu du \text{} est le nom des vecteurs autorisés séparés les uns des autres par des doubles slash. Cet affichage LaTeX doit avoir pour tag vect. Pour affecter ce tag à cet affichage LaTeX, on utilise l'outil protocole, on sélectionne l'affichage LaTeX et on clique sur le bouton Changer le tag.
Attention : Si vous n'affectez pas les tag indiqués à ces deux affichages LaTeX la ressource ne fonctionnera pas.
Dans cette ressource nous avons choisi d'afficher la solution directement sur la figure dans un affichage LaTeX libre.
Dans le protocole de la figure, cet affichage LaTeX est lat6 et a le code LaTeX suivant :
\begin{array}{l}
\If{f1}
{
\overrightarrow {\mathrm{AF}}=\overrightarrow {\mathrm{AG}}+\overrightarrow {\mathrm{GF}}=-\overrightarrow {\mathrm{OC}}+\overrightarrow {\mathrm{OD}}
\\\text{donc }\overrightarrow {\mathrm{AF}}=-\vec{i}+\vec{j}
}
{
\If{f2}
{
\overrightarrow {\mathrm{BD}}=\overrightarrow {\mathrm{BA}}+\overrightarrow {\mathrm{AD}}=-\overrightarrow {\mathrm{OC}}+\overrightarrow {\mathrm{OD}}
\\\text{donc }\overrightarrow {\mathrm{BD}}=-\vec{i}+2\vec{j}
}
{
\If{f3}
{
\overrightarrow {\mathrm{FB}}=\overrightarrow {\mathrm{FG}}+\overrightarrow {\mathrm{GB}}=-\overrightarrow {\mathrm{OD}}+2\overrightarrow {\mathrm{OC}}
\\\text{donc }\overrightarrow {\mathrm{FB}}=2\vec{i}-\vec{j}
}
{
\If{f4}
{
\overrightarrow {\mathrm{EB}}=\overrightarrow {\mathrm{EG}}+\overrightarrow {\mathrm{GB}}=-2\overrightarrow {\mathrm{OD}}+2\overrightarrow {\mathrm{OC}}
\\\text{donc }\overrightarrow {\mathrm{EB}}=2\vec{i}-2\vec{j}
}
{
\If{f5}
{
\overrightarrow {\mathrm{AE}}=\overrightarrow {\mathrm{AG}}+\overrightarrow {\mathrm{GE}}=-\overrightarrow {\mathrm{OC}}+2\overrightarrow {\mathrm{OD}}
\\\text{donc }\overrightarrow {\mathrm{EB}}=-\vec{i}+2\vec{j}
}
{
\If{f6}
{
\overrightarrow {\mathrm{OG}}=\overrightarrow {\mathrm{OA}}+\overrightarrow {\mathrm{AG}}=-\overrightarrow {\mathrm{OD}}-\overrightarrow {\mathrm{OC}}
\\\text{donc }\overrightarrow {\mathrm{OG}}=-\vec{i}-\vec{j}
}
{
\If{f7}
{
\overrightarrow {\mathrm{IA}}=\overrightarrow {\mathrm{IG}}+\overrightarrow {\mathrm{GA}}=-3\overrightarrow {\mathrm{OD}}+\overrightarrow {\mathrm{OC}}
\\\text{donc }\overrightarrow {\mathrm{OG}}=\vec{i}-3\vec{j}
}
{
\If{f8}
{
\overrightarrow {\mathrm{GC}}=\overrightarrow {\mathrm{GB}}+\overrightarrow {\mathrm{BC}}=2\overrightarrow {\mathrm{OC}}+\overrightarrow {\mathrm{OD}}
\\\text{donc }\overrightarrow {\mathrm{GC}}=2\vec{i}+\vec{j}
}
{
\If{f9}
{
\overrightarrow {\mathrm{DG}}=\overrightarrow {\mathrm{DE}}+\overrightarrow {\mathrm{EG}}=-\overrightarrow {\mathrm{OC}}-2\overrightarrow {\mathrm{OD}}
\\\text{donc }\overrightarrow {\mathrm{OG}}=-\vec{i}-2\vec{j}
}
{
\If{f10}
{
\overrightarrow {\mathrm{HE}}=\overrightarrow {\mathrm{HG}}+\overrightarrow {\mathrm{GE}}=-3\overrightarrow {\mathrm{OC}}+2\overrightarrow {\mathrm{OD}}
\\\text{donc }\overrightarrow {\mathrm{HE}}=-3\vec{i}+2\vec{j}
}
{
\If{f11}
{
\overrightarrow {\mathrm{IH}}=\overrightarrow {\mathrm{IG}}+\overrightarrow {\mathrm{GH}}=-3\overrightarrow {\mathrm{OD}}+3\overrightarrow {\mathrm{OC}}
\\\text{donc }\overrightarrow {\mathrm{IH}}=3\vec{i}-3\vec{j}
}
{
\overrightarrow {\mathrm{B\,I}}=\overrightarrow {\mathrm{BG}}+\overrightarrow {\mathrm{GI}}=-2\overrightarrow {\mathrm{OD}}+3\overrightarrow {\mathrm{OD}}
\\\text{donc }\overrightarrow {\mathrm{B\,I}}=-2\vec{i}+3\vec{j}
}
}
}
}
}
}
}
}
}
}
}
\end{array}
Il a été choisi de représenter en rose le vecteur à décomposer (suivant la valeur de f).
Nous allons expliquer sur un exemple comment cela a été fait pour le cas où f a pour valeur 1.
Dans la palette des couleurs on active la couleur magenta et une épaisseur de trait de 2 pixels.
On change provisoirement la formule du calcul f en lui donnant la formule 1 (au lieu de 1+r1). Ceci se fait en utilisant par exemple l'outil protocole ![]() ou l'outil de modification d'objet numérique
ou l'outil de modification d'objet numérique ![]() .
.
On utilise ensuite l'outil homothétie ![]() . On clique sur le point O (centre de l'homthétie).
. On clique sur le point O (centre de l'homthétie).
Une boîte de dialogue demande le rapport de l'homothétie. On entre comme rapport 1/f1 (ce rapport existe et vaut 1 car f = 1 donc f1 = 1) puis on clique sur le point A pour créer son image.
On active ensuite l'outil ![]() de création d'un vecteur puis on clique sur A (en fait sur le point image qu'on vient de créer en spécifiant qu'on voulait cliquer sur un point construit) puis sur F.
de création d'un vecteur puis on clique sur A (en fait sur le point image qu'on vient de créer en spécifiant qu'on voulait cliquer sur un point construit) puis sur F.
On procède ainsi pour le cas suivant en donnant à f la formule 2 (ce qui fait disparaître notre vecteur précédent) et ainsi de suite.
Quand tous les cas ont été traités on redonne à f la formule 1+r1.
Nous allons maintenant expliquer comment faire apparaître lors de la correction l'affichage LaTeX contenant la solution et des éléments visuels supplémentaires.
Au tout début de la figure nous avons créé une variable nommée cor avec comme valeur mini 0, comme valeur maxi 1 et comme pas 1. Elle ne peut donc rendre que les valeurs 0 ou 1.
Nous lui faisons prendre la valeur 1 uniquement lors de la correction.
On utilise l'outil ![]() pour modifier la valeur actuelle de cor et lui donner la valeur 1 et donner provisoirement à f la formule 1 (au lieu de 1+r1).
pour modifier la valeur actuelle de cor et lui donner la valeur 1 et donner provisoirement à f la formule 1 (au lieu de 1+r1).
On utilise ensuite l'outil homothétie ![]() . On clique sur le point O (centre de l'homthétie).
. On clique sur le point O (centre de l'homthétie).
Une boîte de dialogue demande le rapport de l'homothétie. On entre comme rapport on entre 1/(cor&f1) (ce rapport existe et vaut 1 car f = 1 donc f1 = 1) puis on clique sur le point G pour créer son image.
On crée ensuite en marron le vecteur joignant A et de dernier point que nous avons créé (confondu avec G et il faut choisir dernier objet quand il est demandé de choisir).
On crée ensuite un milieu en cliquant sur A puis sur le dernier point créé confondu avec G (là aussi il faut choisir dernier objet quand il est demandé de choisir).
On crée ensuite avec l'outil ![]() un affichage LaTeX lié à ce milieu avec un alignement centré horizontalement et au-dessous verticalement) avec comme code LaTeX :
un affichage LaTeX lié à ce milieu avec un alignement centré horizontalement et au-dessous verticalement) avec comme code LaTeX :
-\vec{i}
On masque ensuite le milieu avec l'outil ![]() .
.
On procède de même ensuite pour créer en vert le vecteur joignant notre dernier point confondu avec G avec le point F, le milieu du segment joignant ces deux points et un affichage LaTeX lié à ce milieu avec comme code LaTeX :
\vec{j}
On procède ensuite de même pour les 11 autres cas en donnant successivement à f les valeurs 2, 3, …, 12.
Quand cela est fini :
On redonne à f la formule 1+r1.
On donne à la variable cor la valeur actuelle 0 (les éléments de correction disparaissent).
Notre figure doit ici comporter une macro d'intitulé solution chargée de faire apparaître les éléments de correction.
Avant de créer cette macro nous créons deux autres macros.
Pour créer ces macros on déroule la barre d'outils des affichages et on clique à sa droite sur l'outil ![]() . ON choisir ensuite le type de macro à créer.
. ON choisir ensuite le type de macro à créer.
On crée d'abord une macro d'apparition d'objets.
On clique à un endroit libre de la figure, on entre dans la boîte de dialogue qui s'ouvre son intitulé (ici voir solution), on clique à un endroit de la figure où sera affiché l'intitulé.
Il est ensuite demandé de cliquer sur les objets que notre macro doit faire apparaître : On clique sur l'affichage LaTeX donnant la correction puis on clique en bas et à droite sur le bouton ![]() pour indiquer que l'on a fini. La macro apparaît.
pour indiquer que l'on a fini. La macro apparaît.
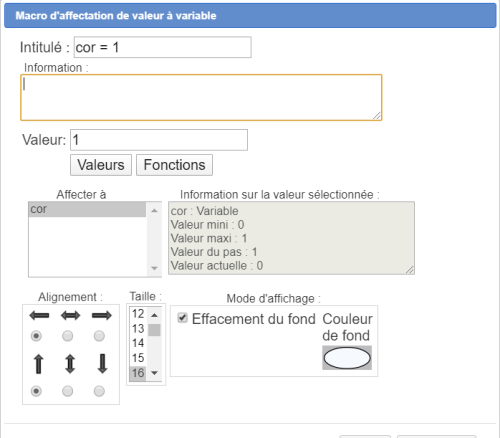
On crée ensuite une macro de type Macro d'affectation de valeur à variable, on clique sur la figure à l'endroit où sera affiché l'intitulé puis on rempli la boîte de dialogue comme ci-dessous :
Cette macro affectera donc la valeur 1 à la variable cor lorsqu'elle sera executée.
Il reste à créer une macro qui va enchaîner l'exécution des deux macros précédentes.
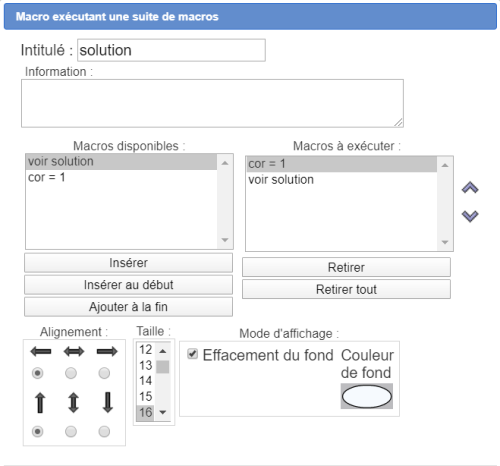
On choisit pour cela de créer une Macro exécutant une suite de macro, on clique à l'endroit où sera affiché son intitulé et on remplit la boîte de dialogue comme ci-dessous :
Attention :Il est impératif que cette dernière macro ait bien pour intitulé solution.
Pour finir :
Il nous reste à donner à la variable cor la valeur 0, à masquer avec l'outil ![]() les trois macros et l'affichage LaTeX de la solution.
les trois macros et l'affichage LaTeX de la solution.
Notre figure est alors prête pour créer la ressource.
Etape 2 : Création de notre ressource dans LaboMep V2.
Connectez vous à LaboMep V2 avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).
Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez par exemple Décomposer un vecteur.
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez les cases seconde et première.
Dans les champs Résumé et Description, entrez Demande de décomposer un vecteur en fonction de deux autres..
En bas de la page, cliquez sur Créer la ressource.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour J3P.
Ensuite faites glisser Exercice de calcul vectoriel dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ nbrepetitions entrez par exemple la valeur 6.
Dans le champ Titre entrez ce qui suit :
Décomposer un vecteur
Laissez le champ validation auto à true
Dans le champ nbEssais entrez la valeur 3. Le paramètre nbchances n'est pas utilisé car validation auto est à true. L'élève pourra donc écrire au maximum trois lignes de calcul pour donner sa réponse en appuyant sur la touche Entrée ou en cliquant sur OK.
Ouvrez la figure que vous avez préparée depuis l'endroit où vous l'aviez sauvegardée et utilisez l'icône ![]() d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure (ou copiez dans le presse papier le code Base 64 donné au début de cet article) .
d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure (ou copiez dans le presse papier le code Base 64 donné au début de cet article) .
Collez ce code Base 64 dans le champ fig.
Laissez les valeur par défaut pour les champs width et height (800 et 600 qui sont les largeurs et hauteurs maxi de la figure en pixels).
Dans le champ entete entrez :
$a
Cela fournit ce qui doit être affiché devant le signe = de l'éditeur. Ici nous demandons que soit récupéré le contenu du premier affichage LaTeX de la figure.
Dans le champ nbLatex entrez la valeur 1 : il n'y a qu'un seul affichage LaTeX récupéré dans la figure, c'est le premier de la figure et il contient le vecteur à décomposer).
Dans le champ charset entrez :
\(\)OABCDEFGHIij0123456789+\-\/
Il s'agit d'une expression régulière donnant les caractères autorisés à la frappe dans l'éditeur.
Dans le champ enonceLigne1 entrez :
On considère la figure ci-dessous formée de triangles équilatéraux. On pose $\\vecteur{\\mathrm{OC}} = \\vecteur{i}$ et $\\vecteur{\\mathrm{OD}} = \\vecteur{j}.$<br>Il faut écrire le vecteur $£a$ sous la forme $a\\vecteur{i}+b\\vecteur{j}$ (écriture la plus simple possible).
Les <br> servent à obtenir un saut à la ligne.
Cochez true pour btnFrac pour autoriser le bouton permettant d'écrire une fraction et false pour tous les autres boutons.
Supprimez le contenu du champ param. Cet exercice n'est pas paramétrable.
Vous pouvez maintenant valider la boîte de dialogue de choix des paramètres.
Ensuite cliquez en bas sur le bouton Enregistrer pour enregistrer votre ressource.
Si vous voulez maintenant tester votre ressource, fermez d’abord l’onglet Décomposer un vecteur puis, dans Mes Ressources, faites un clic droit sur la ressource.
Vous pouvez maintenant tester la ressource.
Rappel des objets que doit absolument contenir votre figure pour une résolution d'inéquation
La figure doit contenir un affichage LaTeX de tag point dont le contenu est \text{Noms des points que l'élève peut utiliser dans les calculs séparés pas des //}.
La figure doit contenir des calculs complexes dont les noms sont les noms des points contenus dans l'affichage LaTeX ci-dessus.
La figure peut contenir un affichage LaTeX de tag vect dont le contenu est \text{Noms des vecteurs sous forme de lettre que l'élève peut utiliser dans sa réponse}.
Si nous désirons que l'élève puisse écrire des vecteurs avec une lettre minuscule sous la flèche elle doit contenir un affichage LaTeX de tag vect dont le contenu est \text{Noms des vecteurs séparés par des //} . La figure doit contenir un calcul complexe (ou une mesure d'affixe) ayant pour nom chacun des noms autorisés pour les vecteurs. Si on autorise un vecteur i à être utilisé, il doit être représenté dans la figure par un calcul complexe nommé i'.
Dans notre exemple, A, B et C étaient choisis de façon aléatoire mais on peut par exemple imaginer un autre type d'exercice où on présente à l'élève un triangle équilatéral ABC. Dans ce cas A, B et C pourraient être les affixes de ces trois points mesurées dans un repère orthonormal.
La figure doit contenir un calcul complexe nommé rep auquel sera affectée la réponse de l'élève.
La figure doit contenir un calcul nommé reponse qui doit valoir 1 si la réponse contenue dans rep correspond à une des formes finales attendues, 2 si la réponse est exacte mais n'est pas finale et 0 si elle est fausse.
Elle doit contenir un affichage LaTeX donnant la solution :
Soit cet affichage LaTeX est affiché par la figure (ce qui est le cas dans notre exemple) auquel cas la figure doit contenir une macro d'intitulé solution faisant paraître cet affichage LaTeX (et éventuellement d'autres objets graphiques nécessaires pour expliquer la correction).
Soit cet affichage LaTeX est affiché à l'extérieur de la figure (au-dessus). Dans ce cas il doit avoir pout tag solution et être formé d'un tableau dont les lignes sont des \text dont le contenu est les lignes à afficher (ce qui est en mode maths étant entouré de caractères $).
Comment se passe l'évaluation de la réponse de l'élève ?
Imaginons que la valeur de f tirée au hasard par la figure est égale à 5. On demande dans ce cas à décomposer le vecteur AE et la bonne réponse est -i+2j.
Si l'élève entre comme réponse 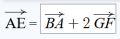 , la ressource va affecter comme formule au calcul complexe rep la formule suivante :
, la ressource va affecter comme formule au calcul complexe rep la formule suivante :
(A-B)+2*(G-F)
Ce calcul n'est pas équivalent au calcul sol5 (qui contient comme formule -i'+2*j) mais, une fois les lettres A, B, G et F remplacées par leur valeur (ici les affixes mesurées), le module de la différence entre rep et sol5 sera considéré comme nul (à epsilon près) et donc le calcul reponse va renvoyer comme valeur 2. la réponse sera acceptée comme exacte mais pas comme finale.
Si la réponse suivante de l'élève est la suivante : 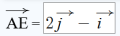 , la ressource va affecter au calcul complexe rep la formule suivante :
, la ressource va affecter au calcul complexe rep la formule suivante :
2*j-i'
i' et j vont être remplacés par leurs valeurs numériques et on va comparer la formule obtenue dans rep avec la formule de sol5 (une fois les valeurs de i' et j remplacées dans sol5).
Les deux calculs étant équivalents, reponse va renvoyer la valeur 1 et la réponse sera acceptée comme finale et exacte.