Table des matières
Produit matriciel
Nous désirons créer une ressource de calcul proposant un calcul matriciel d'une matrice 3 x 3 par une matrice ligne ou colonne (littérale) demandant dans une première étape si le calcul existe et, si, oui demandant dans une deuxième étape les dimensions du produit en enfin le résultat dans une troisième étape.
Pour créer cette ressource vous pouvez utiliser MathGraph32 dans sa version en ligne.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
Etape 1 : Création de la figure MathGraph
Commencez par créer la figure mathgraph.
Si vous désirez sauter ce qui suit vous pouvez utiliser le code Base 64 de la figure ci-dessous et, dans MathGraph32, utiliser l'icône ![]() puis choisir Figure par code Base 64.
puis choisir Figure par code Base 64.
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAUeAAACygAAAQEAAAACAAAABgANSW5pdFJhbmQxMFZhbACISW5pdGllIGxlcyBjYWxjdWxzIGFsw6lhdG9pcmVzIG7DqWNlc3NhaXJlcyDDoCB1bmUgcmVzc291cmNlICBNYXRoR3JhcGgzMiBwb3VyIExhYm9NZXAgdXRpbGlzYW50IE1hdGhHcmFwaDMyIGF2ZWMgMTAgdmFsZXVycyBhbMOpYXRvaXJlcwAAAAEAAAAVAgAAABb#####AAAAAQARQ0VsZW1lbnRHZW5lcmlxdWUACGluaXRyYW5k#####wAAAAH#####AAAAAQAHQ0NhbGN1bAH#####AAVuYnZhcgANMTAraW5pdHJhbmQqMP####8AAAABAApDT3BlcmF0aW9uAP####8AAAABAApDQ29uc3RhbnRlQCQAAAAAAAAAAAACAv####8AAAABAA9DUmVzdWx0YXRWYWxldXIAAAAAAAAAAwAAAAAAAAAAAAAAAQH#####AAZuYmNhczEACGluaXRyYW5kAAAABAAAAAAAAAABAf####8ABm5iY2FzMgAIaW5pdHJhbmQAAAAEAAAAAAAAAAEB#####wAGbmJjYXMzAAhpbml0cmFuZAAAAAQAAAAAAAAAAQH#####AAZuYmNhczQACGluaXRyYW5kAAAABAAAAAAAAAABAf####8ABm5iY2FzNQAIaW5pdHJhbmQAAAAEAAAAAAAAAAEB#####wAGbmJjYXM2AAhpbml0cmFuZAAAAAQAAAAAAAAAAQH#####AAZuYmNhczcACGluaXRyYW5kAAAABAAAAAAAAAABAf####8ABm5iY2FzOAAIaW5pdHJhbmQAAAAEAAAAAAAAAAEB#####wAGbmJjYXM5AAhpbml0cmFuZAAAAAQAAAAAAAAAAQH#####AAduYmNhczEwAAhpbml0cmFuZAAAAAQAAAAAAAAAAQH#####AAJyMQATaW50KHJhbmQoMCkqbmJjYXMxKf####8AAAACAAlDRm9uY3Rpb24CAAAAAgIAAAAFEQAAAAMAAAAAAAAAAD#pZixxZ8soAAAABAAAAAIAAAABAf####8AAnIyABNpbnQocmFuZCgwKSpuYmNhczIpAAAABQIAAAACAgAAAAURAAAAAwAAAAAAAAAAP7b6wqqemYAAAAAEAAAAAwAAAAEB#####wACcjMAE2ludChyYW5kKDApKm5iY2FzMykAAAAFAgAAAAICAAAABREAAAADAAAAAAAAAAA#5PwR5KE0GgAAAAQAAAAEAAAAAQH#####AAJyNAATaW50KHJhbmQoMCkqbmJjYXM0KQAAAAUCAAAAAgIAAAAFEQAAAAMAAAAAAAAAAD#hE7LWkchKAAAABAAAAAUAAAABAf####8AAnI1ABNpbnQocmFuZCgwKSpuYmNhczUpAAAABQIAAAACAgAAAAURAAAAAwAAAAAAAAAAP7dPbPinMAAAAAAEAAAABgAAAAEB#####wACcjYAE2ludChyYW5kKDApKm5iY2FzNikAAAAFAgAAAAICAAAABREAAAADAAAAAAAAAAA#p+BMTI9GAAAAAAQAAAAHAAAAAQH#####AAJyNwATaW50KHJhbmQoMCkqbmJjYXM3KQAAAAUCAAAAAgIAAAAFEQAAAAMAAAAAAAAAAD+pKO4DvBJgAAAABAAAAAgAAAABAf####8AAnI4ABNpbnQocmFuZCgwKSpuYmNhczgpAAAABQIAAAACAgAAAAURAAAAAwAAAAAAAAAAP+Tn2FK#CZgAAAAEAAAACQAAAAEB#####wACcjkAE2ludChyYW5kKDApKm5iY2FzOSkAAAAFAgAAAAICAAAABREAAAADAAAAAAAAAAA#xzp8X9fQQAAAAAQAAAAKAAAAAQH#####AANyMTAAFGludChyYW5kKDApKm5iY2FzMTApAAAABQIAAAACAgAAAAURAAAAAwAAAAAAAAAAP+W#wxQ7VhwAAAAEAAAACwAAAAYAElByZXBhcmF0aW9uM0V0YXBlcwBRQ29uc3RydWl0IGRlcyBvYmpldHMgdXRpbGlzZSDDoCB1bmUgcmVzc291cmNlIGVuIDMgw6l0YXBlcyBiYXPDqWUgc3VyIE1hdGhHcmFwaDMyAAAAAAAAAAQAAAAAB#####8AAAABAA9DVmFyaWFibGVCb3JuZWUB#####wAFZXRhcGU#8AAAAAAAAD#wAAAAAAAAQAgAAAAAAAA#8AAAAAAAAAAAATEAATMAATH#####AAAAAQAfQ01hY3JvQWZmZWN0YXRpb25WYWxldXJWYXJpYWJsZQD#####AQAAAAEAAP####8QQIYIAAAAAABAOdcKPXCj2AIAAAAAAAAAAAAAAAADAAAAAAAAAAAABmV0YXBlMQAAAAAAAz#wAAAAAAAAAAAAAAAAAAcA#####wEAAAABAAD#####EECGCAAAAAAAQExrhR64UewCAAAAAAAAAAAAAAAAAwAAAAAAAAAAAAZldGFwZTIAAAAAAANAAAAAAAAAAAAAAAAAAAAHAP####8BAAAAAQAA#####xBAhggAAAAAAEBV9cKPXCj2AgAAAAAAAAAAAAAAAAMAAAAAAAAAAAAGZXRhcGUzAAAAAAADQAgAAAAAAAAAAAAA#####wAAAAEAEUNNYWNyb1N1aXRlTWFjcm9zAf####8AAAD#AQAA#####xBAiKgAAAAAAEA51wo9cKPYAgAAAAAAAAAAAAAAAAMAAAAAAAAAAAALbWFjcm9FdGFwZTEAAAAAAAEAAAABAAAACAH#####AAAA#wEAAP####8QQIioAAAAAABAS2uFHrhR7AIAAAAAAAAAAAAAAAADAAAAAAAAAAAAC21hY3JvRXRhcGUyAAAAAAABAAAAAgAAAAgB#####wAAAP8BAAD#####EECIqAAAAAAAQFV1wo9cKPYCAAAAAAAAAAAAAAAAAwAAAAAAAAAAAAttYWNyb0V0YXBlMwAAAAAAAQAAAAMAAAABAAAAWP####8AAAABAApDQ2FsY0NvbnN0AP####8AAnBpABYzLjE0MTU5MjY1MzU4OTc5MzIzODQ2AAAAA0AJIftURC0YAAAAAQD#####AAVuYnZhcgACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzMQACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzMgACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzMwACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzNAACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzNQACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzNgACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzNwACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzOAACMTAAAAADQCQAAAAAAAAAAAABAP####8ABm5iY2FzOQACMTAAAAADQCQAAAAAAAAAAAABAP####8AB25iY2FzMTAAATQAAAADQBAAAAAAAAAAAAABAP####8AAnIxABNpbnQocmFuZCgwKSpuYmNhczEpAAAABQIAAAACAgAAAAURAAAAAwAAAAAAAAAAP+qaq2Y0VNgAAAAEAAAAAgAAAAEA#####wACcjIAE2ludChyYW5kKDApKm5iY2FzMikAAAAFAgAAAAICAAAABREAAAADAAAAAAAAAAA#ze+ldD#MWAAAAAQAAAADAAAAAQD#####AAJyMwATaW50KHJhbmQoMCkqbmJjYXMzKQAAAAUCAAAAAgIAAAAFEQAAAAMAAAAAAAAAAD#mzvCWX3i4AAAABAAAAAQAAAABAP####8AAnI0ABNpbnQocmFuZCgwKSpuYmNhczQpAAAABQIAAAACAgAAAAURAAAAAwAAAAAAAAAAP+Ryf8uO3b4AAAAEAAAABQAAAAEA#####wACcjUAE2ludChyYW5kKDApKm5iY2FzNSkAAAAFAgAAAAICAAAABREAAAADAAAAAAAAAAA#2#W1vRlTYAAAAAQAAAAGAAAAAQD#####AAJyNgATaW50KHJhbmQoMCkqbmJjYXM2KQAAAAUCAAAAAgIAAAAFEQAAAAMAAAAAAAAAAD#rgPwEEKusAAAABAAAAAcAAAABAP####8AAnI3ABNpbnQocmFuZCgwKSpuYmNhczcpAAAABQIAAAACAgAAAAURAAAAAwAAAAAAAAAAP9mR9mrLW1AAAAAEAAAACAAAAAEA#####wACcjgAE2ludChyYW5kKDApKm5iY2FzOCkAAAAFAgAAAAICAAAABREAAAADAAAAAAAAAAA#yC2VihtPoAAAAAQAAAAJAAAAAQD#####AAJyOQATaW50KHJhbmQoMCkqbmJjYXM5KQAAAAUCAAAAAgIAAAAFEQAAAAMAAAAAAAAAAD+28KqB2OZwAAAABAAAAAoAAAABAP####8AA3IxMAAUaW50KHJhbmQoMCkqbmJjYXMxMCkAAAAFAgAAAAICAAAABREAAAADAAAAAAAAAAA#sl+KaegxUAAAAAQAAAALAAAAAQD#####AAFhAAJyMQAAAAQAAAAMAAAAAQD#####AAFiAAJyMgAAAAQAAAANAAAAAQD#####AAFjAAJyMwAAAAQAAAAOAAAAAQD#####AAFkAAJyNAAAAAQAAAAPAAAAAQD#####AAFlAAJyNQAAAAQAAAAQAAAAAQD#####AAFmAAJyNgAAAAQAAAARAAAAAQD#####AAFnAAJyNwAAAAQAAAASAAAAAQD#####AAFoAAJyOAAAAAQAAAATAAAAAQD#####AAFqAAJyOQAAAAQAAAAUAAAAAQD#####AANjYXMABTErcjEwAAAAAgAAAAADP#AAAAAAAAAAAAAEAAAAFQAAAAEA#####wAEY2FzMQAFY2FzPTEAAAACCAAAAAQAAAAfAAAAAz#wAAAAAAAAAAAAAQD#####AARjYXMyAAVjYXM9MgAAAAIIAAAABAAAAB8AAAADQAAAAAAAAAAAAAABAP####8ABGNhczMABWNhcz0zAAAAAggAAAAEAAAAHwAAAANACAAAAAAAAAAAAAEA#####wAEY2FzNAAFY2FzPTQAAAACCAAAAAQAAAAfAAAAA0AQAAAAAAAA#####wAAAAEAFENJbXBsZW1lbnRhdGlvblByb3RvAP####8AElByZXBhcmF0aW9uM0V0YXBlcwAAAAMAAAAEAAAAAAAAAAYBAAAAJAAFZXRhcGVAAAAAAAAAAD#wAAAAAAAAQAgAAAAAAAA#8AAAAAAAAAAAATEAATMAATEAAAAHAAAAACQBAAAAAQAA#####xBAhggAAAAAAEA51wo9cKPYAgAAAAAAAAAAAAAAAAMAAAAAAAAAAAAGZXRhcGUxAAAAAAADP#AAAAAAAAAAAAAlAAAABwAAAAAkAQAAAAEAAP####8QQIYIAAAAAABATGuFHrhR7AIAAAAAAAAAAAAAAAADAAAAAAAAAAAABmV0YXBlMgAAAAAAA0AAAAAAAAAAAAAAJQAAAAcAAAAAJAEAAAABAAD#####EECGCAAAAAAAQFX1wo9cKPYCAAAAAAAAAAAAAAAAAwAAAAAAAAAAAAZldGFwZTMAAAAAAANACAAAAAAAAAAAACUAAAAIAQAAACQAAAD#AQAA#####xBAiKgAAAAAAEA51wo9cKPYAgAAAAAAAAAAAAAAAAMAAAAAAAAAAAALbWFjcm9FdGFwZTEAAAAAAAEAAAAmAAAACAEAAAAkAAAA#wEAAP####8QQIioAAAAAABAS2uFHrhR7AIAAAAAAAAAAAAAAAADAAAAAAAAAAAAC21hY3JvRXRhcGUyAAAAAAABAAAAJwAAAAgBAAAAJAAAAP8BAAD#####EECIqAAAAAAAQFV1wo9cKPYCAAAAAAAAAAAAAAAAAwAAAAAAAAAAAAttYWNyb0V0YXBlMwAAAAAAAQAAACgAAAABAP####8ABWNhczIzAAljYXMyfGNhczMAAAACCwAAAAQAAAAhAAAABAAAACIAAAABAP####8ABWNhczM0AAljYXMzfGNhczQAAAACCwAAAAQAAAAiAAAABAAAACMAAAABAP####8ACG5iRXRhcGVzABFzaShjYXMzfGNhczQsMSwzKf####8AAAABAA1DRm9uY3Rpb24zVmFyAAAAAAILAAAABAAAACIAAAAEAAAAIwAAAAM#8AAAAAAAAAAAAANACAAAAAAAAP####8AAAACAAZDTGF0ZXgA#####wAAAAABAAdlbm9uY2Ux#####xBAOAAAAAAAAEA11wo9cKPYAAAAAAAAAAAAAAAAAAIDAAAAAwAAAAAAAAAAAAAAAggAAAAEAAAAJQAAAAM#8AAAAAAAAAIUXGJlZ2lue2FycmF5fXtsfQpcdGV4dHtMZSBjYWxjdWwgbWF0cmljaWVsIHN1aXZhbnQgZXN0LWlsIHZhbGlkZSA#fSAKXFwgXHRleHR7JApcSWZ7Y2FzMjN9CnsKXElme2NhczJ9CnsKXGxlZnQoIFxiZWdpbnttYXRyaXh9eCAmIHkgJiB6IFxlbmR7bWF0cml4fSBccmlnaHQpCn0KewpcbGVmdCggXGJlZ2lue21hdHJpeH14IFxcIHkgXFwgeiBcZW5ke21hdHJpeH0gXHJpZ2h0KQp9Clx0aW1lcwp9CnsKfQpcbGVmdCgKXGJlZ2lue21hdHJpeH0KClxWYWx7YX0gJiBcVmFse2J9ICYgXFZhbHtjfQpcXCBcVmFse2R9ICYgXFZhbHtlfSAmIFxWYWx7Zn0KXFwgXFZhbHtnfSAmIFxWYWx7aH0gJiBcVmFse2p9ClxlbmR7bWF0cml4fQpccmlnaHQpClxJZntjYXMyM30Kewp9CnsKXHRpbWVzIApcSWZ7Y2FzMX0KewpcbGVmdCggXGJlZ2lue21hdHJpeH0geCBcXCB5IFxcIHogXGVuZHttYXRyaXh9IFxyaWdodCkKfQp7ClxsZWZ0KCBcYmVnaW57YXJyYXl9e2x9IHggJiB5ICYgeiBcZW5ke2FycmF5fSBccmlnaHQpCn0KfQokfQpcZW5ke2FycmF5fQAAAAwA#####wAAAAABAAtmb3JtdWxhaXJlMf####8QQD8AAAAAAABAYzrhR64UewAAAAAAAAAAAAAAAAACAwAAAAMAAAAAAAAAAAAAAAIIAAAABAAAACUAAAADP#AAAAAAAAAAF1x0ZXh0e1LDqXBvbnNlIDogbGlzdDF9AAAADAD#####AAAAAAEABmxpc3QxMf####8QQGUgAAAAAABAY3rhR64UewAAAAAAAAAAAAAAAAACAwAAAAMAAAAAAAAAAAAAAAIIAAAABAAAACUAAAADP#AAAAAAAAAANlxiZWdpbnthcnJheX17bH0KXHRleHR7T1VJfSAKXFwgXHRleHR7Tk9OfQpcZW5ke2FycmF5fQAAAAEA#####wAJcmVzTGlzdDExABFzaShjYXMxfGNhczIsMSwyKQAAAAsAAAAAAgsAAAAEAAAAIAAAAAQAAAAhAAAAAz#wAAAAAAAAAAAAA0AAAAAAAAAAAAAADAD#####AAAAAAEAB2Vub25jZTL#####EEA+AAAAAAAAQDfXCj1wo9gAAAAAAAAAAAAAAAAAAgMAAAADAAAAAAAAAAAAAAACCAAAAAQAAAAlAAAAA0AAAAAAAAAAAjBcYmVnaW57YXJyYXl9e2x9Clx0ZXh0e1F1ZWxsZXMgc29udCBsZXMgZGltZW5zaW9ucyBkZSBsYSBtYXRyaWNlIHLDqXN1bHRhdCBkdSBjYWxjdWwgc3VpdmFudCA#fSAKXFwgXHRleHR7JApcSWZ7Y2FzMjN9CnsKXElme2NhczJ9CnsKXGxlZnQoIFxiZWdpbnttYXRyaXh9eCAmIHkgJiB6IFxlbmR7bWF0cml4fSBccmlnaHQpCn0KewpcbGVmdCggXGJlZ2lue21hdHJpeH14IFxcIHkgXFwgeiBcZW5ke21hdHJpeH0gXHJpZ2h0KQp9Clx0aW1lcwp9CnsKfQpcbGVmdCgKXGJlZ2lue21hdHJpeH0KClxWYWx7YX0gJiBcVmFse2J9ICYgXFZhbHtjfQpcXCBcVmFse2R9ICYgXFZhbHtlfSAmIFxWYWx7Zn0KXFwgXFZhbHtnfSAmIFxWYWx7aH0gJiBcVmFse2p9ClxlbmR7bWF0cml4fQpccmlnaHQpClxJZntjYXMyM30Kewp9CnsKXHRpbWVzIApcSWZ7Y2FzMX0KewpcbGVmdCggXGJlZ2lue2FycmF5fXtsfSB4IFxcIHkgXFwgeiBcZW5ke2FycmF5fSBccmlnaHQpCn0KewpcbGVmdCggXGJlZ2lue21hdHJpeH0geCAmIHkgJiB6IFxlbmR7bWF0cml4fSBccmlnaHQpCn0KfQokfQpcZW5ke2FycmF5fQAAAAwA#####wAAAAABAAtmb3JtdWxhaXJlMv####8QQEOAAAAAAABAYhrhR64UewAAAAAAAAAAAAAAAAACAwAAAAMAAAAAAAAAAAAAAAIIAAAABAAAACUAAAADQAAAAAAAAAAARVx0ZXh0e0xlIHLDqXN1bHRhdCBlc3QgdW5lIG1hdHJpY2Ugw6AgZWRpdDEgbGlnbmVzIGV0IGVkaXQyIGNvbG9ubmVzfQAAAAEA#####wAFcmVwMjEAATAAAAADAAAAAAAAAAAAAAABAP####8ABXJlcDIyAAEwAAAAAwAAAAAAAAAAAAAAAQD#####AAhyZXNvbHUyMQAYc2koY2FzMSxyZXAyMT0zLHJlcDIxPTEpAAAACwAAAAAEAAAAIAAAAAIIAAAABAAAADUAAAADQAgAAAAAAAAAAAACCAAAAAQAAAA1AAAAAz#wAAAAAAAAAAAAAQD#####AAhyZXNvbHUyMgAYc2koY2FzMSxyZXAyMj0xLHJlcDIyPTMpAAAACwAAAAAEAAAAIAAAAAIIAAAABAAAADYAAAADP#AAAAAAAAAAAAACCAAAAAQAAAA2AAAAA0AIAAAAAAAAAAAADAD#####AAAAAAEAB2Vub25jZTP#####EEAzAAAAAAAAQEJrhR64UewAAAAAAAAAAAAAAAAAAgMAAAADAAAAAAAAAAAAAAACCAAAAAQAAAAlAAAAA0AIAAAAAAAAAYJcYmVnaW57YXJyYXl9e2x9Clx0ZXh0e0xlIHByb2R1aXQgZCd1bmUgbWF0cmljZSAkXElme2NhczF9ezNcdGltZXMzfXsxXHRpbWVzM30kIHBhciB1bmUgbWF0cmljZSAkXElme2NhczF9ezNcdGltZXMxfXszXHRpbWVzM30kIGVzdCB1bmUgbWF0cmljZSAkXElme2NhczF9ezNcdGltZXMxfXsxXHRpbWVzM30kfSAKXFwgXHRleHR7Yydlc3Qgw6AgZGlyZSB1bmUgbWF0cmljZSDDoCBcSWZ7Y2FzMX17dHJvaXMgbGlnbmVzIGV0IHVuZSBjb2xvbm5lfXt1bmUgbGlnbmUgZXQgdHJvaXMgY29sb25uZXN9Ln0KXFwgXHRleHR7RG9ubmVyIGNpLWRlc3NvdXMgbGEgbWF0cmljZSByw6lzdWx0YXQgc291cyBsYSBmb3JtZSBsYSBwbHVzIHNpbXBsZSBwb3NzaWJsZSA6fQpcZW5ke2FycmF5fQAAAAwA#####wAAAAABAAtmb3JtdWxhaXJlM#####8QQESAAAAAAABAYRrhR64UewAAAAAAAAAAAAAAAAACAwAAAAMAAAAAAAAAAAAAAAIIAAAABAAAACUAAAADQAgAAAAAAAACmFxiZWdpbnthcnJheX17bH0KXHRleHR7JApcSWZ7Y2FzMjN9CnsKXElme2NhczJ9CnsKXGxlZnQoIFxiZWdpbnttYXRyaXh9eCAmIHkgJiB6IFxlbmR7bWF0cml4fSBccmlnaHQpCn0KewpcbGVmdCggXGJlZ2lue21hdHJpeH14IFxcIHkgXFwgeiBcZW5ke21hdHJpeH0gXHJpZ2h0KQp9Clx0aW1lcwp9CnsKfQpcbGVmdCgKXGJlZ2lue21hdHJpeH0KXFZhbHthfSAmIFxWYWx7Yn0gJiBcVmFse2N9ClxcIFxWYWx7ZH0gJiBcVmFse2V9ICYgXFZhbHtmfQpcXCBcVmFse2d9ICYgXFZhbHtofSAmIFxWYWx7an0KXGVuZHttYXRyaXh9ClxyaWdodCkKXElme2NhczIzfQp7Cn0KewpcdGltZXMgClxJZntjYXMxfQp7ClxsZWZ0KCBcYmVnaW57bWF0cml4fSB4IFxcIHkgXFwgeiBcZW5ke21hdHJpeH0gXHJpZ2h0KQp9CnsKXGxlZnQoIFxiZWdpbnttYXRyaXh9IHggJiB5ICYgeiBcZW5ke21hdHJpeH0gXHJpZ2h0KQp9Cn0KPQpcSWZ7Y2FzMX0KewpcbGVmdCgKXGJlZ2lue21hdHJpeH0KXGVkaXRhYmxle30gClxcIFxlZGl0YWJsZXt9ClxcIFxlZGl0YWJsZXt9ClxlbmR7bWF0cml4fQpccmlnaHQpCn0KewpcbGVmdCgKXGJlZ2lue21hdHJpeH0KXGVkaXRhYmxle30gJiBcZWRpdGFibGV7fSAmIFxlZGl0YWJsZXt9ClxlbmR7bWF0cml4fQpccmlnaHQpCn0KJH0KXGVuZHthcnJheX3#####AAAAAQAFQ0ZvbmMA#####wAEemVybwASYWJzKHgpPDAuMDAwMDAwMDAxAAAAAgQAAAAFAP####8AAAACABFDVmFyaWFibGVGb3JtZWxsZQAAAAAAAAADPhEuC+gm1pUAAXgAAAABAP####8AAngxAAwxK3JhbmQoMCkvMTAAAAACAAAAAAM#8AAAAAAAAAAAAAIDAAAABREAAAADAAAAAAAAAAA#1EClqtbaCAAAAANAJAAAAAAAAAAAAAEA#####wACeTEADDErcmFuZCgwKS8xMAAAAAIAAAAAAz#wAAAAAAAAAAAAAgMAAAAFEQAAAAMAAAAAAAAAAD#ozyOhSQgcAAAAA0AkAAAAAAAAAAAAAQD#####AAJ6MQAMMStyYW5kKDApLzEwAAAAAgAAAAADP#AAAAAAAAAAAAACAwAAAAURAAAAAwAAAAAAAAAAP+m8X5amTyYAAAADQCQAAAAAAAAAAAABAP####8AAngyAA4xLjErcmFuZCgwKS8xMAAAAAIAAAAAAz#xmZmZmZmaAAAAAgMAAAAFEQAAAAMAAAAAAAAAAD#lYy7oIKTAAAAAA0AkAAAAAAAAAAAAAQD#####AAJ5MgAOMS4xK3JhbmQoMCkvMTAAAAACAAAAAAM#8ZmZmZmZmgAAAAIDAAAABREAAAADAAAAAAAAAAA#7VBKIx56bgAAAANAJAAAAAAAAAAAAAEA#####wACejIADjEuMStyYW5kKDApLzEwAAAAAgAAAAADP#GZmZmZmZoAAAACAwAAAAURAAAAAwAAAAAAAAAAP+AJu7B1tsoAAAADQCQAAAAAAAD#####AAAAAQAJQ0ZvbmNOVmFyAP####8ADXJlcEVkaXRhYmxlMzEAATAAAAADAAAAAAAAAAAAAAADAAF4AAF5AAF6AAAADwD#####AA1yZXBFZGl0YWJsZTMyAAEwAAAAAwAAAAAAAAAAAAAAAwABeAABeQABegAAAA8A#####wANcmVwRWRpdGFibGUzMwABMAAAAAMAAAAAAAAAAAAAAAMAAXgAAXkAAXoAAAAPAP####8AAmYxAAthKngrYip5K2MqegAAAAIAAAAAAgAAAAACAgAAAAQAAAAWAAAADgAAAAAAAAACAgAAAAQAAAAXAAAADgAAAAEAAAACAgAAAAQAAAAYAAAADgAAAAIAAAADAAF4AAF5AAF6AAAADwD#####AAJmMgALZCp4K2UqeStmKnoAAAACAAAAAAIAAAAAAgIAAAAEAAAAGQAAAA4AAAAAAAAAAgIAAAAEAAAAGgAAAA4AAAABAAAAAgIAAAAEAAAAGwAAAA4AAAACAAAAAwABeAABeQABegAAAA8A#####wACZjMAC2cqeCtoKnkraip6AAAAAgAAAAACAAAAAAICAAAABAAAABwAAAAOAAAAAAAAAAICAAAABAAAAB0AAAAOAAAAAQAAAAICAAAABAAAAB4AAAAOAAAAAgAAAAMAAXgAAXkAAXoAAAAPAP####8AAmcxAAthKngrZCp5K2cqegAAAAIAAAAAAgAAAAACAgAAAAQAAAAWAAAADgAAAAAAAAACAgAAAAQAAAAZAAAADgAAAAEAAAACAgAAAAQAAAAcAAAADgAAAAIAAAADAAF4AAF5AAF6AAAADwD#####AAJnMgALYip4K2UqeStoKnoAAAACAAAAAAIAAAAAAgIAAAAEAAAAFwAAAA4AAAAAAAAAAgIAAAAEAAAAGgAAAA4AAAABAAAAAgIAAAAEAAAAHQAAAA4AAAACAAAAAwABeAABeQABegAAAA8A#####wACZzMAC2MqeCtmKnkraip6AAAAAgAAAAACAAAAAAICAAAABAAAABgAAAAOAAAAAAAAAAICAAAABAAAABsAAAAOAAAAAQAAAAICAAAABAAAAB4AAAAOAAAAAgAAAAMAAXgAAXkAAXoAAAABAP####8AD2V4YWN0RWRpdGFibGUzMQC0c2koY2FzMSx6ZXJvKHJlcEVkaXRhYmxlMzEoeDEseTEsejEpLWYxKHgxLHkxLHoxKSkmemVybyhyZXBFZGl0YWJsZTMxKHgyLHkyLHoyKS1mMSh4Mix5Mix6MikpLHplcm8ocmVwRWRpdGFibGUzMSh4MSx5MSx6MSktZzEoeDEseTEsejEpKSZ6ZXJvKHJlcEVkaXRhYmxlMzEoeDIseTIsejIpLWcxKHgyLHkyLHoyKSkpAAAACwAAAAAEAAAAIAAAAAIK#####wAAAAEADkNBcHBlbEZvbmN0aW9uAAAAOwAAAAIB#####wAAAAEAEkNBcHBlbEZvbmN0aW9uTlZhcgAAAAMAAABCAAAABAAAADwAAAAEAAAAPQAAAAQAAAA+AAAAEQAAAAMAAABFAAAABAAAADwAAAAEAAAAPQAAAAQAAAA+AAAAEAAAADsAAAACAQAAABEAAAADAAAAQgAAAAQAAAA#AAAABAAAAEAAAAAEAAAAQQAAABEAAAADAAAARQAAAAQAAAA#AAAABAAAAEAAAAAEAAAAQQAAAAIKAAAAEAAAADsAAAACAQAAABEAAAADAAAAQgAAAAQAAAA8AAAABAAAAD0AAAAEAAAAPgAAABEAAAADAAAASAAAAAQAAAA8AAAABAAAAD0AAAAEAAAAPgAAABAAAAA7AAAAAgEAAAARAAAAAwAAAEIAAAAEAAAAPwAAAAQAAABAAAAABAAAAEEAAAARAAAAAwAAAEgAAAAEAAAAPwAAAAQAAABAAAAABAAAAEEAAAABAP####8AD2V4YWN0RWRpdGFibGUzMgC0c2koY2FzMSx6ZXJvKHJlcEVkaXRhYmxlMzIoeDEseTEsejEpLWYyKHgxLHkxLHoxKSkmemVybyhyZXBFZGl0YWJsZTMyKHgyLHkyLHoyKS1mMih4Mix5Mix6MikpLHplcm8ocmVwRWRpdGFibGUzMih4MSx5MSx6MSktZzIoeDEseTEsejEpKSZ6ZXJvKHJlcEVkaXRhYmxlMzIoeDIseTIsejIpLWcyKHgyLHkyLHoyKSkpAAAACwAAAAAEAAAAIAAAAAIKAAAAEAAAADsAAAACAQAAABEAAAADAAAAQwAAAAQAAAA8AAAABAAAAD0AAAAEAAAAPgAAABEAAAADAAAARgAAAAQAAAA8AAAABAAAAD0AAAAEAAAAPgAAABAAAAA7AAAAAgEAAAARAAAAAwAAAEMAAAAEAAAAPwAAAAQAAABAAAAABAAAAEEAAAARAAAAAwAAAEYAAAAEAAAAPwAAAAQAAABAAAAABAAAAEEAAAACCgAAABAAAAA7AAAAAgEAAAARAAAAAwAAAEMAAAAEAAAAPAAAAAQAAAA9AAAABAAAAD4AAAARAAAAAwAAAEkAAAAEAAAAPAAAAAQAAAA9AAAABAAAAD4AAAAQAAAAOwAAAAIBAAAAEQAAAAMAAABDAAAABAAAAD8AAAAEAAAAQAAAAAQAAABBAAAAEQAAAAMAAABJAAAABAAAAD8AAAAEAAAAQAAAAAQAAABBAAAAAQD#####AA9leGFjdEVkaXRhYmxlMzMAtHNpKGNhczEsemVybyhyZXBFZGl0YWJsZTMzKHgxLHkxLHoxKS1mMyh4MSx5MSx6MSkpJnplcm8ocmVwRWRpdGFibGUzMyh4Mix5Mix6MiktZjMoeDIseTIsejIpKSx6ZXJvKHJlcEVkaXRhYmxlMzMoeDEseTEsejEpLWczKHgxLHkxLHoxKSkmemVybyhyZXBFZGl0YWJsZTMzKHgyLHkyLHoyKS1nMyh4Mix5Mix6MikpKQAAAAsAAAAABAAAACAAAAACCgAAABAAAAA7AAAAAgEAAAARAAAAAwAAAEQAAAAEAAAAPAAAAAQAAAA9AAAABAAAAD4AAAARAAAAAwAAAEcAAAAEAAAAPAAAAAQAAAA9AAAABAAAAD4AAAAQAAAAOwAAAAIBAAAAEQAAAAMAAABEAAAABAAAAD8AAAAEAAAAQAAAAAQAAABBAAAAEQAAAAMAAABHAAAABAAAAD8AAAAEAAAAQAAAAAQAAABBAAAAAgoAAAAQAAAAOwAAAAIBAAAAEQAAAAMAAABEAAAABAAAADwAAAAEAAAAPQAAAAQAAAA+AAAAEQAAAAMAAABKAAAABAAAADwAAAAEAAAAPQAAAAQAAAA+AAAAEAAAADsAAAACAQAAABEAAAADAAAARAAAAAQAAAA#AAAABAAAAEAAAAAEAAAAQQAAABEAAAADAAAASgAAAAQAAAA#AAAABAAAAEAAAAAEAAAAQf####8AAAAEABBDVGVzdEVxdWl2YWxlbmNlAP####8ABHRlcTEAAABFAAAAQgEAAAAAAz#wAAAAAAAAAQEAAAAAEgD#####AAR0ZXEyAAAARgAAAEMBAAAAAAM#8AAAAAAAAAEBAAAAABIA#####wAEdGVxMwAAAEcAAABEAQAAAAADP#AAAAAAAAABAQAAAAASAP####8ABXRlcScxAAAASAAAAEIBAAAAAAM#8AAAAAAAAAEBAAAAABIA#####wAFdGVxJzIAAABJAAAAQwEAAAAAAz#wAAAAAAAAAQEAAAAAEgD#####AAV0ZXEnMwAAAEoAAABEAQAAAAADP#AAAAAAAAABAQAAAAABAP####8AEHJlc29sdUVkaXRhYmxlMzEAE3NpKGNhczEsdGVxMSx0ZXEnMSkAAAALAAAAAAQAAAAgAAAABAAAAE4AAAAEAAAAUQAAAAEA#####wAQcmVzb2x1RWRpdGFibGUzMgATc2koY2FzMSx0ZXEyLHRlcScyKQAAAAsAAAAABAAAACAAAAAEAAAATwAAAAQAAABSAAAAAQD#####ABByZXNvbHVFZGl0YWJsZTMzABNzaShjYXMxLHRlcTMsdGVxJzMpAAAACwAAAAAEAAAAIAAAAAQAAABQAAAABAAAAFMAAAAMAP####8AAAAAAQAIc29sdXRpb27#####EEA5AAAAAAAAQGz64UeuFHoAAAAAAAAAAAAAAAAAAwAAAAAAAAAAC#dcYmVnaW57YXJyYXl9e2x9ClxJZntjYXMxfQp7Clx0ZXh0e0xlIHByb2R1aXQgZCd1bmUgbWF0cmljZSAkM1x0aW1lczMkIHBhciB1bmUgbWF0cmljZSAkM1x0aW1lczEkfQpcXCBcdGV4dHtlc3QgdW5lIG1hdHJpY2UgJDNcdGltZXMxJCBkb25jIGljaSB1bmUgbWF0cmljZSBjb2xvbm5lIGRlICQzJCDDqWzDqW1lbnRzLn0KXFwgXHRleHR7JApNPVxsZWZ0KCBcYmVnaW57bWF0cml4fQpcdGV4dGNvbG9ye2JsYWNrfXtcVmFse2F9fSAmXHRleHRjb2xvcntibGFja317XFZhbHtifX0gJlx0ZXh0Y29sb3J7YmxhY2t9e1xWYWx7Y319ClxcXHRleHRjb2xvcnttYXJvb259e1xWYWx7ZH19ICZcdGV4dGNvbG9ye21hcm9vbn17XFZhbHtlfX0gJlx0ZXh0Y29sb3J7bWFyb29ufXtcVmFse2Z9fQpcXFx0ZXh0Y29sb3J7Z3JlZW59e1xWYWx7Z319ICAmXHRleHRjb2xvcntncmVlbn17XFZhbHtofX0gJlx0ZXh0Y29sb3J7Z3JlZW59e1xWYWx7an19ClxlbmR7bWF0cml4fSBccmlnaHQpClx0aW1lcwpcbGVmdCggXGJlZ2lue2FycmF5fXtsfQpcdGV4dGNvbG9ye21hZ2VudGF9IHt4fQpcXCBcdGV4dGNvbG9ye21hZ2VudGF9IHt5fQpcXCBcdGV4dGNvbG9ye21hZ2VudGF9IHt6fQpcZW5ke2FycmF5fSBccmlnaHQpCiR9ClxcIFx0ZXh0eyQKTT1cbGVmdCggXGJlZ2lue21hdHJpeH0KXHRleHRjb2xvcntibGFja317XFZhbHthfX1cdGltZXNcdGV4dGNvbG9ye21hZ2VudGF9e3h9K1x0ZXh0Y29sb3J7YmxhY2t9e1xWYWx7Yn19XHRpbWVzXHRleHRjb2xvcnttYWdlbnRhfXt5fStcdGV4dGNvbG9ye2JsYWNrfXtcVmFse2N9fVx0aW1lc1x0ZXh0Y29sb3J7bWFnZW50YX17en0KXFwgXHRleHRjb2xvcnttYXJvb259e1xWYWx7ZH19XHRpbWVzXHRleHRjb2xvcnttYWdlbnRhfXt4fStcdGV4dGNvbG9ye21hcm9vbn17XFZhbHtlfX1cdGltZXNcdGV4dGNvbG9ye21hZ2VudGF9e3l9K1x0ZXh0Y29sb3J7bWFyb29ufXtcVmFse2Z9fVx0aW1lc1x0ZXh0Y29sb3J7bWFnZW50YX17en0KXFwgXHRleHRjb2xvcntncmVlbn17XFZhbHtnfX1cdGltZXNcdGV4dGNvbG9ye21hZ2VudGF9e3h9K1x0ZXh0Y29sb3J7Z3JlZW59e1xWYWx7aH19XHRpbWVzXHRleHRjb2xvcnttYWdlbnRhfXt5fStcdGV4dGNvbG9ye2dyZWVufXtcVmFse2p9fVx0aW1lc1x0ZXh0Y29sb3J7bWFnZW50YX17en0KXGVuZHttYXRyaXh9IFxyaWdodCkKJH0KXFwgXHRleHR7JApNPVxsZWZ0KCBcYmVnaW57bWF0cml4fQpcRm9yU2ltcHtmMX0KXFwgXEZvclNpbXB7ZjJ9ClxcIFxGb3JTaW1we2YzfQpcZW5ke21hdHJpeH0gXHJpZ2h0KQokfQp9CnsKXElme2NhczJ9CnsKXHRleHR7TGUgcHJvZHVpdCBkJ3VuZSBtYXRyaWNlICQxXHRpbWVzMyQgcGFyIHVuZSBtYXRyaWNlICQzXHRpbWVzMyR9ClxcIFx0ZXh0e2VzdCB1bmUgbWF0cmljZSAkMVx0aW1lczMkICBkb25jIGljaSB1bmUgbWF0cmljZSBsaWduZSBkZSAkMyQgw6lsw6ltZW50cy59ClxcIFx0ZXh0eyQKTT1cbGVmdCggXGJlZ2lue21hdHJpeH0KXHRleHRjb2xvcnttYWdlbnRhfXt4fSAmIFx0ZXh0Y29sb3J7bWFnZW50YX17eX0gJiBcdGV4dGNvbG9ye21hZ2VudGF9e3p9ClxlbmR7bWF0cml4fSBccmlnaHQpClx0aW1lcwpcbGVmdCggXGJlZ2lue21hdHJpeH0KXHRleHRjb2xvcntibGFja317XFZhbHthfX0gJlx0ZXh0Y29sb3J7bWFyb29ufXtcVmFse2J9fSAmXHRleHRjb2xvcntncmVlbn17XFZhbHtjfX0KXFxcdGV4dGNvbG9ye2JsYWNrfXtcVmFse2R9fSAmXHRleHRjb2xvcnttYXJvb259e1xWYWx7ZX19ICZcdGV4dGNvbG9ye2dyZWVufXtcVmFse2Z9fQpcXFx0ZXh0Y29sb3J7YmxhY2t9e1xWYWx7Z319ICZcdGV4dGNvbG9ye21hcm9vbn17XFZhbHtofX0gJlx0ZXh0Y29sb3J7Z3JlZW59e1xWYWx7an19ClxlbmR7bWF0cml4fSBccmlnaHQpCiR9ClxcIFx0ZXh0eyQKTT1cbGVmdCggXGJlZ2lue21hdHJpeH0KXHRleHRjb2xvcnttYWdlbnRhfXt4fVx0aW1lc1x0ZXh0Y29sb3J7YmxhY2t9e1xWYWx7YX19K1x0ZXh0Y29sb3J7bWFnZW50YX17eX1cdGltZXNcdGV4dGNvbG9ye2JsYWNrfXtcVmFse2R9fStcdGV4dGNvbG9ye21hZ2VudGF9e3p9XHRpbWVzXHRleHRjb2xvcntibGFja317XFZhbHtnfX0KJiAgXHRleHRjb2xvcnttYWdlbnRhfXt4fVx0aW1lc1x0ZXh0Y29sb3J7bWFyb29ufXtcVmFse2J9fStcdGV4dGNvbG9ye21hZ2VudGF9e3l9XHRpbWVzXHRleHRjb2xvcnttYXJvb259e1xWYWx7ZX19K1x0ZXh0Y29sb3J7bWFnZW50YX17en1cdGltZXNcdGV4dGNvbG9ye21hcm9vbn17XFZhbHtofX0KJiAgXHRleHRjb2xvcnttYWdlbnRhfXt4fVx0aW1lc1x0ZXh0Y29sb3J7Z3JlZW59e1xWYWx7Y319K1x0ZXh0Y29sb3J7bWFnZW50YX17eX1cdGltZXNcdGV4dGNvbG9ye2dyZWVufXtcVmFse2Z9fStcdGV4dGNvbG9ye21hZ2VudGF9e3p9XHRpbWVzXHRleHRjb2xvcntncmVlbn17XFZhbHtqfX0KXGVuZHttYXRyaXh9IFxyaWdodCkKJH0KXFwgXHRleHR7JApNPVxsZWZ0KCBcYmVnaW57bWF0cml4fQpcRm9yU2ltcHtnMX0KJiBcRm9yU2ltcHtnMn0KJiBcRm9yU2ltcHtnM30KXGVuZHttYXRyaXh9IFxyaWdodCkKJH0KfQp7Clx0ZXh0e0xlIHByb2R1aXQgZGUgbWF0cmljZXMgY2ktZGVzc291cyBuJ2V4aXN0ZSBwYXMgY2FyIGxlIG5vbWJyZSBkZSBjb2xvbm5lc30KXFwgXHRleHR7ZGUgbGEgcHJlbWnDqHJlIG1hdHJpY2Ugbidlc3QgcGFzIMOpZ2FsZSBhdSBub21icmUgZGUgbGlnbmVzIGRlIGxhIGRldXhpw6htZS59ClxcIFx0ZXh0eyQKXElme2NhczN9CnsKXGxlZnQoIFxiZWdpbnttYXRyaXh9eCBcXCB5IFxcIHogXGVuZHttYXRyaXh9IFxyaWdodCkKXHRpbWVzCn0Kewp9ClxsZWZ0KApcYmVnaW57bWF0cml4fQoKXFZhbHthfSAmIFxWYWx7Yn0gJiBcVmFse2N9ClxcIFxWYWx7ZH0gJiBcVmFse2V9ICYgXFZhbHtmfQpcXCBcVmFse2d9ICYgXFZhbHtofSAmIFxWYWx7an0KXGVuZHttYXRyaXh9ClxyaWdodCkKXElme2NhczN9CnsKfQp7Clx0aW1lcyAKXGxlZnQoIFxiZWdpbnttYXRyaXh9IHggJiB5ICYgeiBcZW5ke21hdHJpeH0gXHJpZ2h0KQp9CiR9Cn0KfSAKXGVuZHthcnJheX3###############8=
Nous vous proposons de télécharger ci-dessous une bibliothèque de macro constructions qui vont nous simplifier un peu la tâche. Cliquez sur le lien ci-dessous pour télécharger le fichier zip, et décompressez le dans le dossier de votre choix. Les fichiers contenant des macro constructions MathGraph32 ont le suffixe mgc.
Une fois le logiciel démarré, cliquez sur l'icône ![]() et choisissez de créer une figure sans repère et sans longueur unité.
et choisissez de créer une figure sans repère et sans longueur unité.
Incorporons dans notre figure deux macro constructions de façon à pouvoir l'utiliser par la suite.
Pour pouvoir utiliser ces macro construction dans MathGraph32, cliquez d'abord sur l'icône ![]() qui fait apparaître des icônes supplémentaires.
qui fait apparaître des icônes supplémentaires.
Cliquez ensuite sur l'icône ![]() (gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
(gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
Allez dans le dossier où vous avez décompressé le fichier zip contenant les constructions et cliquez sur le fichier nommé InitRand10Val.mgc puis validez.
Procédez de même pour incorporer dans la figure la macro construction du fichier nommé Preparation3Etapes.
Ces deux constructions font maintenant partie de votre figure.
Pour implémenter notre première construction, nous avons besoin de créer un calcul provisoire. Sa valeur importe peu.
Déroulez la barre des calculs et utilisez l'icône ![]() pour créer un calcul nommé par exemple prov et avec comme formule 1.
pour créer un calcul nommé par exemple prov et avec comme formule 1.
Cliquez ensuite sur l'icône ![]() (gestion des constructions) et choisissez l'item Implémenter une construction de la figure.
(gestion des constructions) et choisissez l'item Implémenter une construction de la figure.
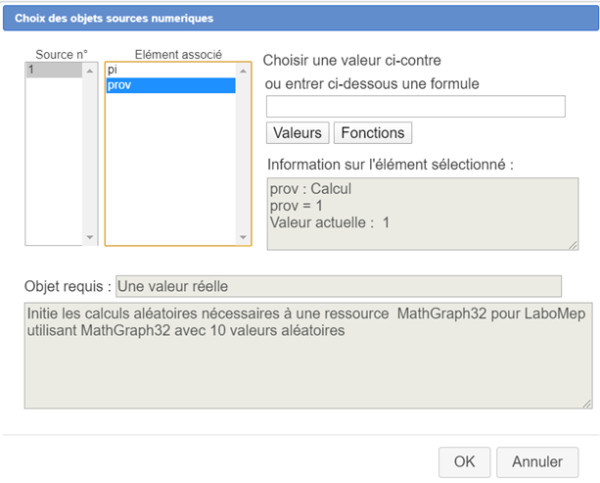
Dans la boîte de dialogue qui s'ouvre, sélectionnez InitRand10Val et cliquez sur le bouton Implémenter.
Une nouvelle boîte de dialogue s'ouvre.
Comme ci-dessous, affectez le calcul prov comme objet source n°1 (c'est le seul) et validez.
Notre macro construction a créé un calcul nbvar de valeur 10, 10 calculs nommés nbcas1 à nbcas10 et 10 calculs nommés r1 à r10.
Pourquoi ici 10 calculs de chaque sorte ?
Notre matrice de 3 lignes et 3 colonnes correspondra à 9 de ces calculs et nous réservons l dixième pour illustrer un des quatre cas de produit matriciel qui sera proposé à l'élève.
La présence de ces calculs permettra, lors de répétitions successives de l'exercice, de ne jamais avoir deux fois les mêmes valeurs proposées.
Mais nous devons modifier certains de ces calculs pour les adapter à la situation prévue.
Ces calculs étant des objets finaux de macro constructions, ils ne sont pour le moment pas modifiables.
Il y a une solution à cela : les transformer en des objets normaux.
Pour cela utilisez l'icône ![]() et cliquez sur l'item Fusionner les constructions implémentées de la figure.
et cliquez sur l'item Fusionner les constructions implémentées de la figure.
Dans la barre supérieure utilisez l'outil ![]() (modification d'objet numérique) et modifiez les formules comme indiqué ci-dessous :
(modification d'objet numérique) et modifiez les formules comme indiqué ci-dessous :
| Nom du calcul | Ancienne formule | Nouvelle formule |
|---|---|---|
| nbvar | 10+prov*0 | 10 |
| nbcas1 | prov | 10 |
| nbcas2 | prov | 10 |
| nbcas3 | prov | 10 |
| nbcas4 | prov | 10 |
| nbcas5 | prov | 10 |
| nbcas6 | prov | 10 |
| nbcas7 | prov | 10 |
| nbcas8 | prov | 10 |
| nbcas9 | prov | 10 |
| nbcas10 | prov | 4 |
La macro a aussi créé des calculs .nommés r1 à r10. Par exemple, r1 contiendra une valeur aléatoire comprise entre 0 et nbcas1
Utilisez maintenant l'outil ![]() pour créer les calculs réels suivants.
pour créer les calculs réels suivants.
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| a | r1 | Sera le terme ligne 1 colonne 1 de la matrice |
| b | r2 | Sera le terme ligne 1 colonne 2 de la matrice |
| c | r3 | Sera le terme ligne 1 colonne 3 de la matrice |
| d | r4 | Sera le terme ligne 2 colonne 1 de la matrice |
| e | r5 | Sera le terme ligne 2 colonne 2 de la matrice |
| f | r6 | Sera le terme ligne 2 colonne 3 de la matrice |
| g | r7 | Sera le terme ligne 3 colonne 1 de la matrice |
| h | r8 | Sera le terme ligne 3 colonne 2 de la matrice |
| j | r9 | Sera le terme ligne 3 colonne 3 de la matrice. A noter qu'un calcul ne peut pas être nommé i qui est réservé pour les nombres complexes |
| cas | 1+r10 | Prendra comme valeurs entières de 1 à 4. Utilisé pour gérer les 4 cas proposés. |
| cas1 | cas=1 | Vaudra 1 quand cas est égal à 1 et 0 sinon |
| cas2 | cas=2 | Vaudra 1 quand cas est égal à 2 et 0 sinon |
| cas3 | cas=3 | Vaudra 1 quand cas est égal à 3 et 0 sinon |
| cas4 | cas=4 | Vaudra 1 quand cas est égal à 4 et 0 sinon |
| cas23 | cas2|cas3 | Vaudra 1 quand cas vaut 2 ou 3 ce qui correspondra au cas où la matrice 3 x 3 est le terme de droite de la multiplication |
| cas34 | cas3|cas4 | Vaudra 1 quand le produi des deux matrices n'existe pas |
| nbEtapes | si(cas3|cas4,1,3) | Dans les cas 3 et 4, le calcul matriciel n'existe pas donc une seule étape sinon 3 étapes |
Nous allons maintenant implémenter la deuxième construction qui va nous aider à gérer les 3 étapes de l'exercice.
Utilisez l'icône ![]() et cliquez sur l'item Implémenter une construction de la figure.
et cliquez sur l'item Implémenter une construction de la figure.
Cette fois sélectionnez la construction nommée Preparation3Etapes et cliquez sur le bouton Implémenter.
Comme précédemment, choisissez comme objet source n°1 le calcul prov et validez. Si vous cliquez sur l'outil ![]() vous verrez qu'elle a créé une variable nommée etape de valeur maxi 3 et de valeur actuelle 1. Elle a aussi créé
un calcul nbEtapes1 qui ne servira pas ici car nous avons déjà créé un calcul nommé nbEtapes. Ce calcul contient comme formule 3+0*prov. Vous pouvez supprimer ce calcul ici inutile.
vous verrez qu'elle a créé une variable nommée etape de valeur maxi 3 et de valeur actuelle 1. Elle a aussi créé
un calcul nbEtapes1 qui ne servira pas ici car nous avons déjà créé un calcul nommé nbEtapes. Ce calcul contient comme formule 3+0*prov. Vous pouvez supprimer ce calcul ici inutile.
Vous pouvez maintenant sélectionner le calcul nommé prov et cliquer sur le bouton Supprimer. Si un message vous avertit que d'autres objets seront supprimés, c'est que vous avez oublié de modifier une des formules ci-dessus ou que vous n'avez pas supprimé le calcul nbEtapes1.
Elle a aussi ajouté à la figure 3 macros d'intitulé macroEtape1, macroEtape2 et macroEtape3 qui serviront à donner à la variable étape les valeurs 1, 2 et 3 respectivement et des affichages LaTeX dans lesquels nous devrons rentrer les énoncés à chaque étape et les formulaires.
Pour pouvoir modifier ces objets il faut à nouveau cliquer sur l'outil ![]() de gestion des constructions et cliquer sur l'item Fusionner les constructions implémentées de la figure.
de gestion des constructions et cliquer sur l'item Fusionner les constructions implémentées de la figure.
Normalement, après l'implémentation de la construction, la variable etape a pour valeur 1. Si ce n'est pas le cas, activez dans la varre supérieure l'outil ![]() et cliquez sur la macro d'intitulé macroEtape1.
et cliquez sur la macro d'intitulé macroEtape1.
La macro construction a créé pour vous un affichage LaTeX de tag enonce1 que vous voyez sur la figure. Son contenue actuel est le suivant :
\begin{array}{l}
\text{Première ligne de l'énoncé à l'étape 1}
\\ \text{Deuxième ligne de l'énoncé à l'étape 1}
\end{array}
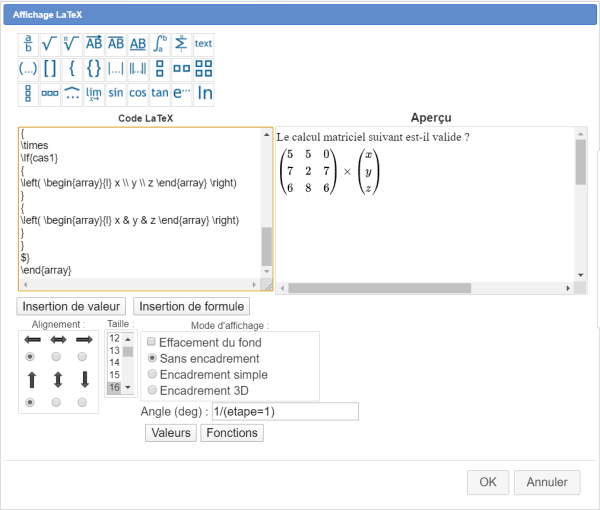
Cliquez sur l'icône ![]() (modification d'objet graphique) puis sur l'affichage LaTex et modifiez la boîte de dialogue comme ci-dessous comme ci-dessous. Seul le contenu du code LaTeX est à changer (l'aperçu peut être différent suivant les valeurs des tirages aléatoires). Vous pouvez vous aider des boutons en haut de la fenêtre. N'oubliez pas en bas d'entrer dans le champ Angle d'affichage La formule 0/(etape=1). Vous pouvez copier-coller le contenu fourni ci-dessous pour le code LaTeX.
(modification d'objet graphique) puis sur l'affichage LaTex et modifiez la boîte de dialogue comme ci-dessous comme ci-dessous. Seul le contenu du code LaTeX est à changer (l'aperçu peut être différent suivant les valeurs des tirages aléatoires). Vous pouvez vous aider des boutons en haut de la fenêtre. N'oubliez pas en bas d'entrer dans le champ Angle d'affichage La formule 0/(etape=1). Vous pouvez copier-coller le contenu fourni ci-dessous pour le code LaTeX.
Le code LaTeX :
\begin{array}{l}
\text{Le calcul matriciel suivant est-il valide ?}
\\ \text{$
\If{cas23}
{
\If{cas2}
{
\left( \begin{matrix}x & y & z \end{matrix} \right)
}
{
\left( \begin{matrix}x \\ y \\ z \end{matrix} \right)
}
\times
}
{
}
\left(
\begin{matrix}
\Val{a} & \Val{b} & \Val{c}
\\ \Val{d} & \Val{e} & \Val{f}
\\ \Val{g} & \Val{h} & \Val{j}
\end{matrix}
\right)
\If{cas23}
{
}
{
\times
\If{cas1}
{
\left( \begin{matrix} x \\ y \\ z \end{matrix} \right)
}
{
\left( \begin{matrix} x & y & z \end{matrix} \right)
}
}
$}
\end{array}
Pour résumer :
- cas1 : matrice 3 x 3 à gauche, matrice colonne x y z à droite
- cas2 : matrice ligne x y z à gauche, matrice 3 x 3 à droite
- cas3 : matrice colonne x y z à gauche, matrice 3 x 3 à droite (n'existe pas)
- cas4 : matrice 3 x 3 à gauche, matrice ligne x y z à droite (n'existe pas)
Une remarque : Pourquoi la macro construction a-t-elle mis 1 comme formule 0/(etape=1) dans le champ Angle de cet affichage LaTeX ?
Il s'agit d'une astuce : quand la variable etape ne vaudra plus 1, cet affichage LaTeX aura un angle avec l'horizontale qui n'existe pas et donc l'affichage LaTeX ne sera plus visible sur la figure, sinon l'angle sera nul par rapport à l'horizontale ce qui est la valeur usuelle. Cela rend la préparation des étapes successives plus facile.
La macro construction a aussi affecté un tag enonce1 à cet affichage LaTeX. Cela permettra à laboMep de le reconnaître comme énoncé à l'étape 1 (l'affectation d'un tag se fait via l'outil protocole ![]() en sélectionnant l'objet et en cliquant sur le bouton Modifier le tag mais ici vous n'avez rien à faire).
en sélectionnant l'objet et en cliquant sur le bouton Modifier le tag mais ici vous n'avez rien à faire).
Il nous faut modifier l'affichage LaTeX destiné à fournir le formulaire que l'élève doit remplir à l'étape 1. Il est présent sur la figure et a été créé par la macro construction. Mais il est probablement masqué par la macro donnant l'énoncé que nous venons de modifier.
Utilisez l'outil ![]() pour déplacer l'affichage LaTeX précédent de façon à rendre à nouveau visible l'autre affichage LaTeX.
pour déplacer l'affichage LaTeX précédent de façon à rendre à nouveau visible l'autre affichage LaTeX.
Cliquez à nouveau sur l'icône ![]() de modification d'objet graphique et cliquez sur ce deuxième affichage LaTeX pour modifier son code.
de modification d'objet graphique et cliquez sur ce deuxième affichage LaTeX pour modifier son code.
Le code actuel est :
\text{Entrer ici le formulaire à l'étape 1}
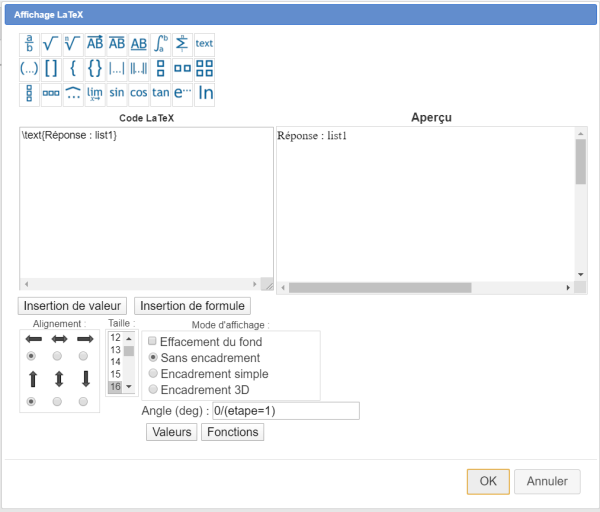
Voici ci-dessous le nouveau code LaTeX à utiliser :
\text{Réponse : list1}
Ce formulaire ne contiendra qu'une seule liste déroulante, repérée par list1 dans le code LaTeX.
Il nous faut créer un autre affichage LaTeX chargé de fournir les items de cette liste.
Utilisez de nouveau l'outil ![]() (affichage LaTeX libre) et cliquez à droite de l'affichage LaTeX précédent.
(affichage LaTeX libre) et cliquez à droite de l'affichage LaTeX précédent.
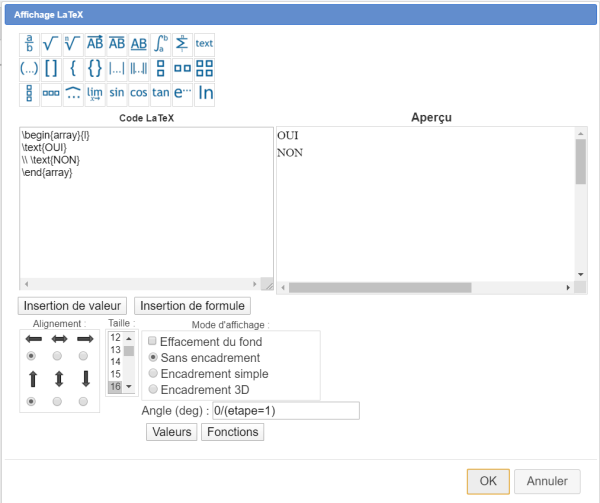
Remplissez la boîte de dialogue comme ci-dessous,avec la formule 0/(etape=1) dans le champ Angle. Utiliser cette formule dans le champ Angle n'est pas indispensable mais fera disparaître cet affichage LaTeX quand nous préparerons les étapes suivantes.
Voici le code LaTeX à utiliser :
\begin{array}{l}
\text{OUI}
\\ \text{NON}
\end{array}
Le contenu de chaque \text de ce code fournit un item de la liste (donc ici les items OUI et NON).
Nous devons lui affecter le tag list11 (le premier chiffre 1 car on est à l'étape 1 et le deuxième car c'est la première liste du formulaire 1 (il n'y en a qu'une). Pour cela, activez dans la barre d'outil supérieure l'outil protocole ![]() , sélectionnez cet affichage LaTeX en bas de la liste des objets puis cliquez sur le bouton Changer le tag pour lui affecter le tag list11.
, sélectionnez cet affichage LaTeX en bas de la liste des objets puis cliquez sur le bouton Changer le tag pour lui affecter le tag list11.
Nous devons aussi fournir un calcul donnant la bonne réponse pour cette liste.
Utilisez l'icône ![]() et créez un calcul nommé resList11 avec comme formule :
et créez un calcul nommé resList11 avec comme formule :
si(cas1|cas2,1,2)
Ainsi si le calcul cas vaut 1 ou 2 on revoie 1 (indice de la réponse oui) et sinon 2 (indice de la réponse NON).
Nous allons passer à la préparation l'étape 2.
Pour cela, activez dans la barre supérieure l'outil ![]() (exécution de macro) et cliquez sur la macro d'intitulé macroEtape2.
(exécution de macro) et cliquez sur la macro d'intitulé macroEtape2.
Exécuter cette macro a donné à la variable etape la valeur 2 et, ainsi, les affichages LaTeX précédents ont disparu (ils n'existent momentanément plus, tant que etape ne vaudra pas 1).
D'autres affichages LaTeX sont apparus permettant de donner l'énoncé et le formulaire à l'étape 2.
Dans l'énoncé à afficher à l'étape 2, nous allons afficher à nouveau le produit matriciel précédent mais en demandant les dimensions de la matrice résultat. Nous pouvons donc copier-coller une partie du contenu du premier énoncé.
Utilisez l'icône ![]() et cliquez sur l’affichage LaTeX contenant le code LaTeX provisoire.
et cliquez sur l’affichage LaTeX contenant le code LaTeX provisoire.
Voici le code LaTeX à utiliser. C'est le même que le précédent à l'exception de la seconde ligne du code LaTeX mais cette fois entrez dans le champ Angle la formule 0/(etape=2):
\begin{array}{l}
\text{Quelles sont les dimensions de la matrice résultat du calcul suivant ?}
\\ \text{$
\If{cas23}
{
\If{cas2}
{
\left( \begin{matrix}x & y & z \end{matrix} \right)
}
{
\left( \begin{matrix}x \\ y \\ z \end{matrix} \right)
}
\times
}
{
}
\left(
\begin{matrix}
\Val{a} & \Val{b} & \Val{c}
\\ \Val{d} & \Val{e} & \Val{f}
\\ \Val{g} & \Val{h} & \Val{j}
\end{matrix}
\right)
\If{cas23}
{
}
{
\times
\If{cas1}
{
\left( \begin{array}{l} x \\ y \\ z \end{array} \right)
}
{
\left( \begin{matrix} x & y & z \end{matrix} \right)
}
}
$}
\end{array}
Il nous faut maintenant modifier le formulaire à l'étape2 qui a été créé par la macro construction.
Déplacez l'affichage LaTeX vers le haut pour le rendre visible, et utilisez l'outil ![]() pour modifier son code LaTeX et le remplacer par le code LaTeX suivant:
pour modifier son code LaTeX et le remplacer par le code LaTeX suivant:
\text{Le résultat est une matrice à edit1 lignes et edit2 colonnes}
Ce formulaire comportera donc deux éditeurs de formule (on est en mode texte) repérés dans le code LaTeX par edit1 et edit2.
Nous devons fournir deux calculs nommés resolu21 et resolu22 qui devront prendre comme valeur 1 si la réponse est la réponse attendue et O sinon. Nous ne donnerons pas à l'utilisateur la possibilité d'utiliser autre chose que des chiffres dans la réponse (sinon nous pourrions aussi définir des calculs nommés exact21 et exact22 qui prendraient pour valeur 1 quand la réponse est bonne mais n'est pas nécessairement la réponse attendue comme dans d'autres ressources). Le premier chiffre 2 correspond à l'étape N°2 et le chiffre suivante est l'indice de l'éditeur de formule dans le formulaire.
Utilisez donc l'outil ![]() pour créer les calculs suivants :
pour créer les calculs suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| rep21 | 0 | Est destiné à contenir a réponse de l'élève dans le premier éditeur |
| rep22 | 0 | Est destiné à contenir a réponse de l'élève dans le deuxième éditeur |
| resolu21 | si(cas1,rep21=3,rep21=1) | Dans le cas 1 la matrice trois lignes, dans le cas 2 une ligne |
| resolu22 | si(cas1,rep22=1,rep22=3) | Dans le cas 1 la matrice à une colonne, dans le cas 2 trois colonnes |
Il faut maintenant nous attaquer à l'étape 3 où on demande à l'élève de donner la matrice résultat.
Activez l'outil ![]() d'exécution de macro et cliquez sur la macro d'intitulé macroEtape3. Nos affichages LaTeX précédents disparaissent (la variable etape a maintenant pour valeur 3).
d'exécution de macro et cliquez sur la macro d'intitulé macroEtape3. Nos affichages LaTeX précédents disparaissent (la variable etape a maintenant pour valeur 3).
Sont apparus deux nouveaux affichages LaTeX destinés à fournir l'énoncé et le formulaire à l'étape 3.
Procédez de même que précédemment pour changer leur code LaTeX en utilisant l'outil ![]()
Voici le code LaTeX pour l'énoncé à l'étape 3 :
\begin{array}{l}
\text{Le produit d'une matrice $\If{cas1}{3\times3}{1\times3}$ par une matrice $\If{cas1}{3\times1}{3\times3}$ est une matrice $\If{cas1}{3\times1}{1\times3}$}
\\ \text{c'est à dire une matrice à \If{cas1}{trois lignes et une colonne}{une ligne et trois colonnes}.}
\\ \text{Donner ci-dessous la matrice résultat sous la forme la plus simple possible :}
\end{array}
Voici le code LaTeX utilisé pour le formulaire à l'étape 3 (il reprend une bonne partie du code LaTeX du premier énoncé) :
\begin{array}{l}
\text{$
\If{cas23}
{
\If{cas2}
{
\left( \begin{matrix}x & y & z \end{matrix} \right)
}
{
\left( \begin{matrix}x \\ y \\ z \end{matrix} \right)
}
\times
}
{
}
\left(
\begin{matrix}
\Val{a} & \Val{b} & \Val{c}
\\ \Val{d} & \Val{e} & \Val{f}
\\ \Val{g} & \Val{h} & \Val{j}
\end{matrix}
\right)
\If{cas23}
{
}
{
\times
\If{cas1}
{
\left( \begin{matrix} x \\ y \\ z \end{matrix} \right)
}
{
\left( \begin{matrix} x & y & z \end{matrix} \right)
}
}
=
\If{cas1}
{
\left(
\begin{matrix}
\editable{}
\\ \editable{}
\\ \editable{}
\end{matrix}
\right)
}
{
\left(
\begin{matrix}
\editable{} & \editable{} & \editable{}
\end{matrix}
\right)
}
$}
\end{array}
Quelques explications concernant ce code LaTeX :
Cette fois les éditeurs de formule ne sont pas en mode texte mais en mode Maths (ils sont entre des caractères $). Ils sont repérés par des \editable{} non numérotés. Dans le formulaire ils seront dans un même bloc (avec un clavier virtuel commun aux trois éditeurs). De façon interne ils sont numérotés de 1 à 3 par ordre croissant d'apparition (attention pour les matrices ils sont numérotés par colonnes et non par lignes ceci pour assurer une compatibilité avec les anciens éditeurs de formule MathQuill mais ici cela importe peu car nous avons à entrer une matrice ligne ou une matrice colonne).
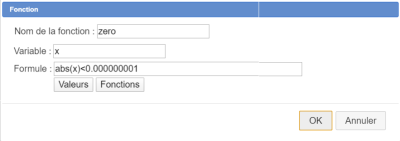
Déroulez la barre d'outils des calculs et utilisez l'icône ![]() pour créer comme ci-dessous une fonction réelle nommée zero avec la formule ci-dessous :
pour créer comme ci-dessous une fonction réelle nommée zero avec la formule ci-dessous :
abs(x)<0.000000001
Utilisez maintenant l'outil ![]() pour créer les calculs réels suivants qui nous serviront à vérifier à 'epsilon' près la validité des réponses dans chacun des éditeurs.
pour créer les calculs réels suivants qui nous serviront à vérifier à 'epsilon' près la validité des réponses dans chacun des éditeurs.
| Nom du calcul | Formule | Commentaire |
|---|
| x1 | 1+rand(0)/10 | Nombre aléatoire compris entre 1 et 1.1 |
| y1 | 1+rand(0)/10 | Nombre aléatoire compris entre 1 et 1.1 |
| z1 | 1+rand(0)/10 | Nombre aléatoire compris entre 1 et 1.1 |
| x2 | 1.1+rand(0)/10 | Nombre aléatoire compris entre 1.1 et 1.2 |
| y2 | 1.1+rand(0)/10 | Nombre aléatoire compris entre 1.1 et 1.2 |
| z2 | 1.1+rand(0)/10 | Nombre aléatoire compris entre 1.1 et 1.2 |
Créons maintenant six fonctions réelles des 3 variables x, y et z correspondant aux réponses attendues dans les trois termes de la matrice résultat pour les cas 1 et le cas 2.
Pour créer une fonction réelle de trois variables vous devez dérouler la barre des calculs et, à sa droite, cliquer sur l'icône ![]() qui propose des outils supplémentaires.
qui propose des outils supplémentaires.
Dans la liste proposée cliquez sur Fonction réelle de trois variables ou plus.
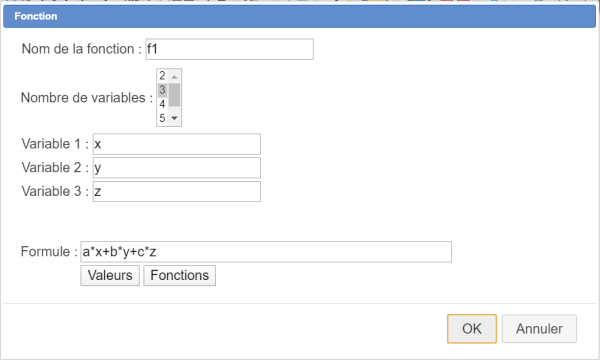
Ci-dessous la boîte de dialogue obtenue quand on crée la fonction f1.
Une fois la première fonction de trois variables créée, utilisez la touche de fonction F2 qui réactive l'outil précédent.
| Nom de la fonction de x, y et z | Formule | Commentaire |
|---|---|---|
| repEditable31 | 0 | est destinée à contenir la réponse de l'élève dans le premier editable |
| repEditable32 | 0 | est destinée à contenir la réponse de l'élève dans le second editable |
| repEditable33 | 0 | est destinée à contenir la réponse de l'élève dans le troisième editable |
| f1 | a*x+b*y+c*z | Correspond à la réponse attendue dans le premier editable du cas 1 |
| f2 | d*x+e*y+f*z | Correspond à la réponse attendue dans le second editable du cas 1 |
| f3 | g*x+h*y+j*z | Correspond à la réponse attendue dans le troisième editable du cas 1 |
| g1 | a*x+d*y+g*z | Correspond à la réponse attendue dans le premier editable du cas 2 |
| g2 | b*x+e*y+h*z | Correspond à la réponse attendue dans le second editable du cas 2 |
| g3 | c*x+f*y+j*z | Correspond à la réponse attendue dans le troisième editable du cas 2 |
Utilisez maintenant l'icône pour créer les calculs réels suivants qui serviront à vérifier si la réponse dans chaque éditeur est bonne (mais pas si la réponse est la réponse finale attendue).
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| exactEditable31 | si(cas1,zero(repEditable31(x1,y1,z1)-f1(x1,y1,z1))&zero(repEditable31(x2,y2,z2)-f1(x2,y2,z2)),zero(repEditable31(x1,y1,z1)-g1(x1,y1,z1))&zero(repEditable31(x2,y2,z2)-g1(x2,y2,z2))) | Vaudra 1 si la réponse du premier éditeur est bonne et 0 sinon |
| exactEditable32 | si(cas1,zero(repEditable32(x1,y1,z1)-f2(x1,y1,z1))&zero(repEditable32(x2,y2,z2)-f2(x2,y2,z2)),zero(repEditable32(x1,y1,z1)-g2(x1,y1,z1))&zero(repEditable32(x2,y2,z2)-g2(x2,y2,z2))) | Vaudra 1 si la réponse du deuxième éditeur est bonne et 0 sinon |
| exactEditable33 | si(cas1,zero(repEditable33(x1,y1,z1)-f3(x1,y1,z1))&zero(repEditable33(x2,y2,z2)-f3(x2,y2,z2)),zero(repEditable33(x1,y1,z1)-g3(x1,y1,z1))&zero(repEditable33(x2,y2,z2)-g3(x2,y2,z2))) | Vaudra 1 si la réponse du deuxième éditeur est bonne et 0 sinon |
Enfin il nous faut vérifier si les réponses données sont bien les réponses attendues, simplifiées au maximum. Pour cela nous allons utiliser des tests d'équivalence.
Pour créer un test d'équivalence, il faut dérouler la barre des calculs, cliquer à sa droite sur l'icône ![]() et cliquer sur l'item Test d'équivalence.
et cliquer sur l'item Test d'équivalence.
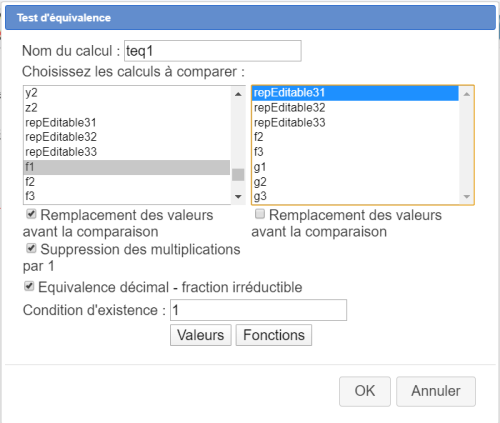
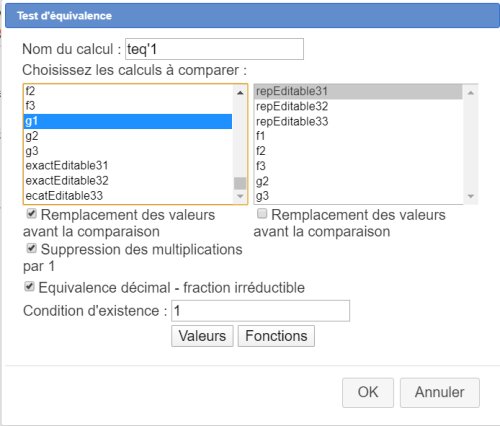
Créez un premier test d'équivalence nommé teq1 entre f1 et repEditable31 comme ci-dessous :
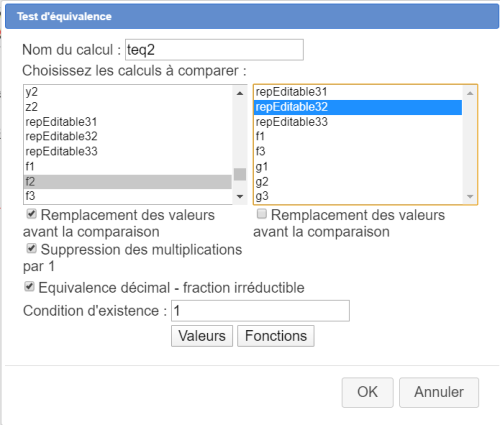
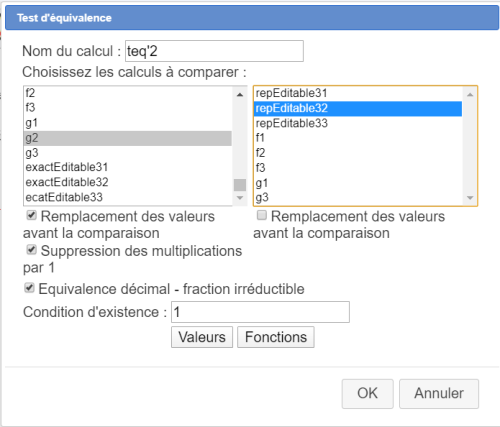
Créez un test d'équivalence nommé teq2 entre f2 et repEditable32 comme ci-dessous :
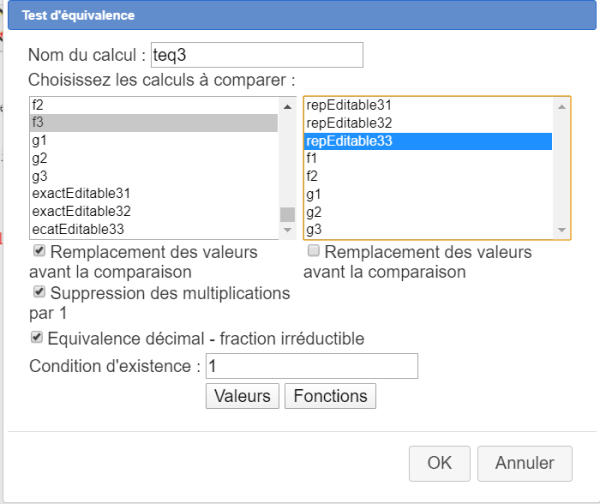
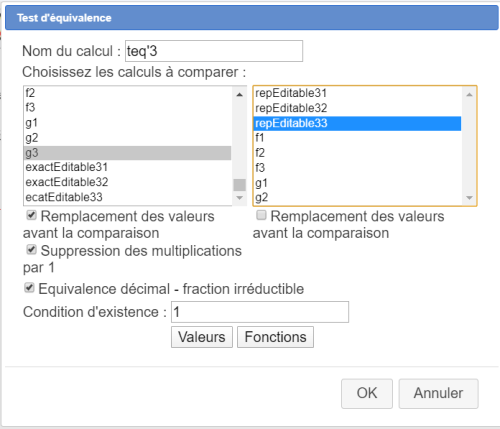
Créez un test d'équivalence nommé teq3 entre f3 et repEdiable33 comme ci-dessous :
Créez un test d'équivalence nommé teq'1 entre g1 et repEditable31 comme ci-dessous :
Créez un test d'équivalence nommé teq'2 entre g2 et repEditable32 comme ci-dessous :
Enfin créez un test d'équivalence nommé teq'3 entre g3 et repEdiable33 comme ci-dessous :
Il nous reste à créer trois calculs destinés à informer Labomep si la réponse finale a été donnée dans les trois éditeurs.
Utilisez l'icône ![]() pour créer les calculs suivants :
pour créer les calculs suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| resoluEditable31 | si(cas1,teq1,teq'1) | Vaut 1 si la première réponse est la réponse attendue |
| resoluEditable32 | si(cas1,teq2,teq'2) | Vaut 1 si la deuxième réponse est la réponse attendue |
| resoluEditable33 | si(cas1,teq3,teq'3) | Vaut 1 si la troisième réponse est la réponse attendue |
Il nous reste à fournir un affichage LaTeX qui fournira la solution de l'exercice.
Cet affichage LaTeX est présent sur la figure depuis le début. S'il est masque par des affichages LaTex d'énoncé et de formulaires, déplacez les avec l'outil ![]() .
.
Son code LaTeX provisoire est :
\begin{array}{l}
\text{Première ligne de la solution}
\\ \text{Deuxième ligne de la solution}
\end{array}
Mais depuis sa création lors de l'implémentation de la macro, d'autres éléments ont été créés qui vont être utilisés par cet affichage LaTeX.
Utilisez pour cela l'outil ![]() (reclassement d'objet graphique vers la fin) et cliquez sr l'affichage LaTeX.
(reclassement d'objet graphique vers la fin) et cliquez sr l'affichage LaTeX.
Remplacez son code LaTeX par le par le code LaTeX suivant :
\begin{array}{l}
\If{cas1}
{
\text{Le produit d'une matrice $3\times3$ par une matrice $3\times1$}
\\ \text{est une matrice $3\times1$ donc ici une matrice colonne de $3$ éléments.}
\\ \text{$
M=\left( \begin{matrix}
\textcolor{black}{\Val{a}} &\textcolor{black}{\Val{b}} &\textcolor{black}{\Val{c}}
\\\textcolor{maroon}{\Val{d}} &\textcolor{maroon}{\Val{e}} &\textcolor{maroon}{\Val{f}}
\\\textcolor{green}{\Val{g}} &\textcolor{green}{\Val{h}} &\textcolor{green}{\Val{j}}
\end{matrix} \right)
\times
\left( \begin{array}{l}
\textcolor{magenta} {x}
\\ \textcolor{magenta} {y}
\\ \textcolor{magenta} {z}
\end{array} \right)
$}
\\ \text{$
M=\left( \begin{matrix}
\textcolor{black}{\Val{a}}\times\textcolor{magenta}{x}+\textcolor{black}{\Val{b}}\times\textcolor{magenta}{y}+\textcolor{black}{\Val{c}}\times\textcolor{magenta}{z}
\\ \textcolor{maroon}{\Val{d}}\times\textcolor{magenta}{x}+\textcolor{maroon}{\Val{e}}\times\textcolor{magenta}{y}+\textcolor{maroon}{\Val{f}}\times\textcolor{magenta}{z}
\\ \textcolor{green}{\Val{g}}\times\textcolor{magenta}{x}+\textcolor{green}{\Val{h}}\times\textcolor{magenta}{y}+\textcolor{green}{\Val{j}}\times\textcolor{magenta}{z}
\end{matrix} \right)
$}
\\ \text{$
M=\left( \begin{matrix}
\ForSimp{f1}
\\ \ForSimp{f2}
\\ \ForSimp{f3}
\end{matrix} \right)
$}
}
{
\If{cas2}
{
\text{Le produit d'une matrice $1\times3$ par une matrice $3\times3$}
\\ \text{est une matrice $1\times3$ donc ici une matrice ligne de $3$ éléments.}
\\ \text{$
M=\left( \begin{matrix}
\textcolor{magenta}{x} & \textcolor{magenta}{y} & \textcolor{magenta}{z}
\end{matrix} \right)
\times
\left( \begin{matrix}
\textcolor{black}{\Val{a}} &\textcolor{maroon}{\Val{b}} &\textcolor{green}{\Val{c}}
\\\textcolor{black}{\Val{d}} &\textcolor{maroon}{\Val{e}} &\textcolor{green}{\Val{f}}
\\\textcolor{black}{\Val{g}} &\textcolor{maroon}{\Val{h}} &\textcolor{green}{\Val{j}}
\end{matrix} \right)
$}
\\ \text{$
M=\left( \begin{matrix}
\textcolor{magenta}{x}\times\textcolor{black}{\Val{a}}+\textcolor{magenta}{y}\times\textcolor{black}{\Val{d}}+\textcolor{magenta}{z}\times\textcolor{black}{\Val{g}}
& \textcolor{magenta}{x}\times\textcolor{maroon}{\Val{b}}+\textcolor{magenta}{y}\times\textcolor{maroon}{\Val{e}}+\textcolor{magenta}{z}\times\textcolor{maroon}{\Val{h}}
& \textcolor{magenta}{x}\times\textcolor{green}{\Val{c}}+\textcolor{magenta}{y}\times\textcolor{green}{\Val{f}}+\textcolor{magenta}{z}\times\textcolor{green}{\Val{j}}
\end{matrix} \right)
$}
\\ \text{$
M=\left( \begin{matrix}
\ForSimp{g1}
& \ForSimp{g2}
& \ForSimp{g3}
\end{matrix} \right)
$}
}
{
\text{Le produit de matrices ci-dessous n'existe pas car le nombre de colonnes}
\\ \text{de la première matrice n'est pas égale au nombre de lignes de la deuxième.}
\\ \text{$
\If{cas3}
{
\left( \begin{matrix}x \\ y \\ z \end{matrix} \right)
\times
}
{
}
\left(
\begin{matrix}
\Val{a} & \Val{b} & \Val{c}
\\ \Val{d} & \Val{e} & \Val{f}
\\ \Val{g} & \Val{h} & \Val{j}
\end{matrix}
\right)
\If{cas3}
{
}
{
\times
\left( \begin{matrix} x & y & z \end{matrix} \right)
}
$}
}
}
\end{array}
La figure est prête. Il est conseillé de l'enregistrer par précaution.
Il est inutile ici de cacher nos affichages LaTeX donnant les énoncés, formulaires et autres et les macros permettant de changer d'étape car la figure n'a pas ici à être affichée. Il le faudrait si notre exercice utilisait comme support la figure MathGraph32.
Etape 2 : Création de notre ressource dans LaboMep
Connectez vous à LaboMep avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).
Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez par exemple Pourcentages : retrouver une valeur de départ..
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez la case Seconde.
Dans les champs Résumé et Description, entrez Demande de trouver un pourcentage d'augmentation ou diminution et de retrouver une valeur initiale.
En bas de la page, cliquez sur Créer la ressource.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour J3P.
Ensuite faites glisser Exercice de calcul multi-éditeurs et multi-étapes dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ Titre entrez ce qui suit :
Le produit d'une matrice 3×3 par une matrice colonne existe-t-il ?
Dans le champ nbrepetitions entrez la valeur 4.
Ouvrez la figure principale depuis l'endroit où vous l'aviez sauvegardée et utilisez l'icône ![]() d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
Collez ce code Base 64 dans le champ fig après avoir cliqué sur le bouton Saisie brute.
Dans les champs width et height entrez 0 (la figure n'a pas à être affichée ellle sert juste à donner énoncés, formulaires, solution et vérifier les réponses).
Dans le champ param entrez une chaîne vide (cet exercice ne sera pas paramétrable.
Dans le champ nbEssais1 entrez 1 : Un seul essai pour répondre à la question OUI-NON du début.
Dans le champ nbEssais2 entrez 1 : Un seul essai pour donner les dimensions de la matrice produit.
Dans le champ nbEssais3 entrez 1 : Deux essai pour donner la matrice produit.
Dans le champ charset2, entrez : \d (il s'agit des caractères au clavier permis pour la première étape, seulement des chiffres pour entrer les dimensions de la matrice.)
Dans le champ charset3, entrez : xyz\d+-*/²^() (caractères autorisés pour donner la réponse finale)
Tous les boutons btnFrac et suivants doivent être décochés. Pas de formule à entrer pour cette ressource.
Validez les autres paramètres tel quels.
Dans l'éditeur de graphe, cliquez droit sur le nœud principal et renommez le Produit d'une matrice 3×3 par une matrice ligne ou colonne
Cliquez ensuite en bas sur le bouton Enregistrer pour sauvegarder votre ressource.
Vous pouvez maintenant tester votre ressource.
Si quelque chose ne fonctionne pas bien il faudra reprendre la figure MathGraph32, la corriger et modifier le paramètre fig de la figure.
Une dernière remarque sur l'utilité d'avoir utilisé une macro construction pour créer les calculs nbavr, nbcas1, …, nbcas10, r1, …, r10.
Lors de nos quatre répétitions nous sommes assurés que la marice 3×3 n'aura jamais les mêmes termes e, surtout, lors des quatre répétitions, nous aurons les quatre cas prévus : deux où le produit n'existe pas et deux où le produit existe, un avec la matrice 3×3 à gauche du produit et l'autre avec la matrice 3×3 à droite.