Centre d'aide

Commencez par créer la figure mathgraph.

Cette figure doit vérifier un certain nombre de propriétés pour en faire un exercice de calcul.

En particulier, notre figure devra contenir un calcul nommé reponse qui vaudra

• 0 si la réponse est fausse
• 1 si la réponse de l’élève est bonne et écrite sous la forme demandée
• 2 si elle est exacte mais pas écrite sous la forme demandée

Cet exercice demandera de calculer l'intégrale de 0 à k de la fonction f définie par f(x)=e^(x*ln(a)). On demandera à l'élève d'exprimer cette intégrale en fonction de a (k étant une constante pouvant être égale à 1, 2 ou 3).

Le nombre de paramètres aléatoires de la figure sera ici de 1 (seul k pourra varier de façon aléatoire). Pour cela notre figure devra contenir un calcul nommé nbvar contenant la valeur 1 et un calcul nommé r1 chargé du tirage aléatoire et un autre calcul nbcas1 contenant le nombre de valeurs que peuvent prendre le calcul r1.

Pour éviter que la figure obtenue ne soit trop grande pour LaboMep, utilisez l'icône d'options de la barre d'outils supérieure et cochez la case Afficher un cadre de dimensions données puis entrez 700 et 600 dans les champs Largeur et hauteur puis validez. Un cadre grisé apparaît. Vous devrez prendre garde que tous les éléments créés restent bien dans ce cadre.

Dans MathGraph32, utilisez l'icône de création d'une nouvelle figure et cliquez sur l'item Figure sans repère et sans longueur unité.

Dans la barre d'outils supérieure, utilisez l'icône (options de la figure). Cliquez sur l'item Couleur de fond de la figure et entrez dans le champ d'édition #f6fafe.

Créez un calcul nommé nbvar (icône dans la troisième rangée d'icônes à partir du bas réservée aux calculs) contenant comme formule 1. Ce sera le nombre de paramètres aléatoires de notre exercice.

Créez de même un autre calcul réel nommé nbcas1 avec comme formule 3.

Créez un calcul réel nommé r1 contenant comme formule int(rand(0)*nbcas1).

Ainsi le calcul r1 pourra prendre 3 valeurs entières (0, 1 ou 2).

Un calcul nommé k contenant comme formule : 1 + r1.

Déroulez la barre d'icones des calculs (la troisième à partir du bas) et cliquez à l'extrémité droite sur l'icône . Cette icône sert à faire apparaître des outils supplémentaires moins souvent utilisés.

Une boîte de dialogue s'ouvre. Choisissez dans la liste Fonction réelle de deux variables et validez.

Une nouvelle boîte de dialogue s'ouvre pour vous permettre dé définir la fonction.

• Dans le champ Nom de la fonction, entrez txt.
• Dans le champ Variable 1, entrez e
• Dans le champ Variable 2, entrez a
• Dans le champ Formule, entrez la formule ci-dessous :

  integrale(e^(x*ln(a)),x,0,k)

Un affichage LaTeX de la formule de txt devra être contenu dans la figure et sera fourni à LaboMep.

Cet affichage LaTeX doit être le premier affichage LaTeX de la figure (il sera possible de le reclasser si ce n’est pas le cas).

Utilisez l’icône pour créer un affichage LaTeX libre en haut et à droite de la figure avec comme code LaTeX : \ForSimp{txt}.

Pour obtenir de code \ForSimp{}, vous pouvez utiliser le bouton Insertion de formule et cliquer sur txt dans la liste proposée.

Le code LaTeX \ForSimp est un code LaTeX interne à MathGraph32 qui demande ici d’écrire la formule du calcul eq sous la forme la plus simple possible. Le code LaTeX de cet affichage sera récupéré par LaboMep pour afficher la consigne de l’exercice.

Nous allons maintenant mettre en place les éléments de calcul servant à analyser la réponse de l'élève.

Créez de nouveau une fonction réelle de deux variables que devra être nommée rep. C'est la formule de rep qui sera fournie par LaboMep à la figure MathGraph32 pour analyser la réponse de l'élève.

• Dans le champ Nom de la fonction, entrez rep.
• Dans le champ Variable 1, entrez e
• Dans le champ Variable 2, entrez a
• Dans le champ Formule, entrez 0

Nous allons maintenant créer deux fonctions de deux variables qui correspondront aux réponses finales attendues.

Créer une nouvelle fonction de deux variables :

• Dans le champ Nom de la fonction, entrez sol1.
• Dans le champ Variable 1, entrez e
• Dans le champ Variable 2, entrez a
• Dans le champ Formule, entrez la formule ci-dessous

  (a^k-1)/ln(a)

Pour créer une nouvelle fonction de deux variables vous pouvez utiliser la touche de raccourci F2 qui réactive le dernier outil.

Pour cette nouvelle fonction :

• Dans le champ Nom de la fonction, entrez sol2.
• Dans le champ Variable 1, entrez e
• Dans le champ Variable 2, entrez a
• Dans le champ Formule, entrez la formule ci-dessous

  a^k/ln(a)-1/ln(a)

Nous allons maintenant créer deux tests d'équivalence :

Déroulez la barre d'icones des calculs (la troisième à partir du bas) et cliquez à l'extrémité droite sur l'icône .

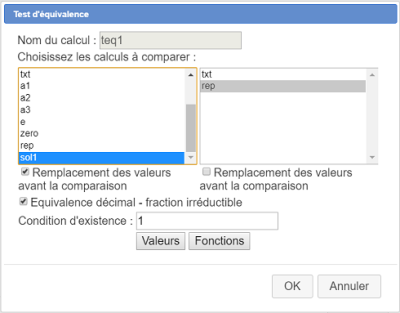
Cette fois choisissez dans la liste Test d'équivalence et complétez la boîte de dialogue comme ci-dessous :

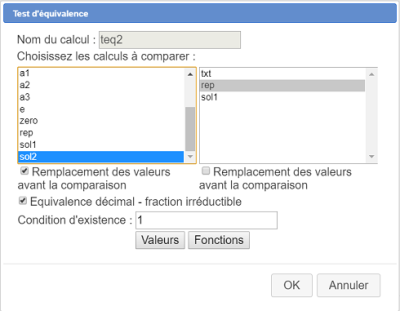
De même créez un deuxième test d'équivalence comme ci-dessous :

Dans la barre d'icônes de calcul, cliquez sur l'icône de création d'un calcul réel et créez un calcul nommé resolu aevc la formule ci-dessous (le caractère | est l'opérateur booléen ou) :

teq1|teq2

Ainsi resolu contiendra 1 si au moins un des deux test d'équivalence est égal à 1.

Nous devons aussi savoit si le calcul rpoposé par l'élève est exact, mais pas terminé.

Nous allons pour cela utiliser des calculs approchés.

Dans la barre d'icônes de calcul, cliquez sur l'icône de création d'une fonction réelle d'une variable.

• Dans le champ Nom de la fonction, entrez zero.
• Dans le champ Variable, entrez x
• Dans le champ Formule, entrez la formule ci-dessous

  abs(x)<0.00000001

Maintenant créez trois calculs réels (icône nommés a1, a2 et a3 avec comme formules respectives :

1+rand(0)/10

1+2*rand(0)/10

1+3*rand(0)/10

Ainsi a1 sera un nombre aléatoire compris entre 1 et 1,1 (exclu), a2 sera lui compris entre 1,1 et 1,2 et a3 entre 1,3 et 1,4.

Créez un calcul réel nommé e avec comme formule :

exp(1)

. Ainsi e contient la base du logarithme népérien.

Créez un nouveau calcul réel nommé exact avec la formule ci-dessous :

zero(rep(e,a1)-sol1(e,a1))&zero(rep(e,a2)-sol1(e,a2))&zero(rep(e,a3)-sol1(e,a3))

Ainsi le calcul exact vaudra 1 si, à 0,00000001 près, la réponse de l'élève est confondue avec la solution pour nos trois valeurs choisies de façon aléatoire.

Dans ces exercices de calcul, la figure doit obtenir un calcul nommé reponse qui vaut 1 si la réponse finale a été entrée, 2 si la réponse est bonne mais n'est pas finale et 0 sinon.

Créez donc un calcul réel nommé reponse avec la formule ci-dessous :

si(resolu,1,si(exact,2,0))

Cette formule utilise la fonction si de MathGraph32 qui est une fonction de trois variables.

Il nous reste à préparer les éléments de correction de notre figure.

Nos explications seront dans un affichage LaTeX qui sera dévoilà au moment de la correction de l'exercice.

Cet affichage LaTeX utilisera des affichages de formules de fonctions que nous allons maintenant créer.

Créez une fonction réelle de deux variables nommée for1 :

• Dans le champ Nom de la fonction, entrez for1.
• Dans le champ Variable 1, entrez e
• Dans le champ Variable 2, entrez a
• Dans le champ Formule, entrez la formule ci-dessous

  1/ln(a)*primitive(e^(x*ln(a)),x,0,k)

Une deuxième nommée for2 :

• Dans le champ Nom de la fonction, entrez for2.
• Dans le champ Variable 1, entrez e
• Dans le champ Variable 2, entrez a
• Dans le champ Formule, entrez la formule ci-dessous

  1/ln(a)*(e^(k*ln(a))-e^0)

Une troisième nommée for3 :

• Dans le champ Nom de la fonction, entrez for3.
• Dans le champ Variable 1, entrez e
• Dans le champ Variable 2, entrez a
• Dans le champ Formule, entrez la formule ci-dessous

  1/ln(a)*((e^ln(a))^k-1)

Créez une fonction réelle d'une variable nommée for4 (icône ) :

• Dans le champ Nom de la fonction, entrez for4.
• Dans le champ Variable , entrez a
• Dans le champ Formule, entrez la formule ci-dessous

  1/ln(a)*(a^k-1)

Dans la palette des couleurs, activez la couleur bleue et activez l'outil de création d'un affichage LaTeX libre outillatex.png32 (dans la barre d'iôones des affichages, quatrième à partir du bas)..

Cliquez en haut et à droite de la figure.

Notre affichage utilisera une matrice pour afficher des lignes. Vous devez donc commencer par cliquer sur l'icône .

Par défaut deux lignes sont prévues. La deuxième commnce par deux caractères slash. Pour rajouter des lignes vous devrez rajouter à chaque fois les deux caractères slash.

Pour passer en mode texte, cliquez sur l'icône .

Pour les affichages de formules, vous pouvez utiliser le bouton Insertion de formule.

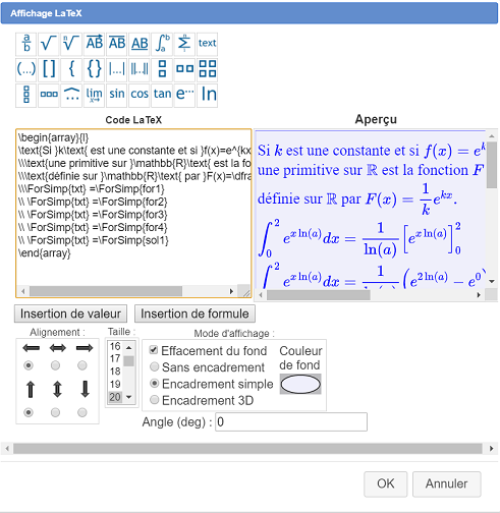
Pour gagner du temps voici ci-dessous le contenu du code LaTeX :

\begin{array}{l}
\text{Si }k\text{ est une constante et si }f(x)=e^{kx},
\\\text{une primitive sur }\mathbb{R}\text{ est la fonction }F
\\\text{définie sur }\mathbb{R}\text{ par }F(x)=\dfrac{1}{k}e^{kx}.
\\\ForSimp{txt} =\ForSimp{for1}
\\ \ForSimp{txt} =\ForSimp{for2}
\\ \ForSimp{txt} =\ForSimp{for3}
\\ \ForSimp{txt} =\ForSimp{for4}
\\ \ForSimp{txt} =\ForSimp{sol1}
\end{array}

Vous pouvez aussi changer la couleur de fond (les exercices de LabOMep utilisent tous la même et cocher la case Encadrement simple comme ci-dessous :