Ceci est une ancienne révision du document !
Exercice de calcul vectoriel (2)
Notre but est créer dans LaboMep un exercice analogue à cet exercice.
Une figure étant donnée à l'élève on lui demande d'exprimer en vecteur donné en fonction de deux vecteurs nommés i et j.
Pour créer cette ressource vous devez utiliser la version JavaScript de MathGraph32, version 6.6.0 ou ultérieure, ou utiliser la version en ligne sur le site de MathGraph32.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé avec prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé avec prise en charge des nombres complexes.
La mise en place de cette ressource étant un peu compliquée, ik est conseillé d'avoir au préalable lu ce tutoriel
Etape 1 : Création de la figure MathGraph
Dans ce tutoriel nous allons fournir la figure ci-dessous en Base 64 et expliquer les grandes lignes de sa création sans expliquer tous les détails.
Voici donc ci-dessous le code Base 64 de cette figure :
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcvb6#gEA#wEAAAAAAAAAAAPZAAACpQAAAQEAAAAAAAAAAAAAAS7#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAPQ1ZhcmlhYmxlQm9ybmVlAP####8AA2NvcgAAAAAAAAAAAAAAAAAAAAA#8AAAAAAAAD#wAAAAAAAAAAABMAABMQABMf####8AAAABAA9DQ2FsY3VsQ29tcGxleGUA#####wAFdmVjdDAAATAAAAABAAAAAAAAAAD#####AAAAAQAHQ0NhbGN1bAD#####AAVuYnZhcgABMQAAAAE#8AAAAAAAAAAAAAQA#####wAGbmJjYXMxAAIxMgAAAAFAKAAAAAAAAAAAAAQA#####wACcjEAE2ludChyYW5kKDApKm5iY2FzMSn#####AAAAAgAJQ0ZvbmN0aW9uAv####8AAAABAApDT3BlcmF0aW9uAgAAAAURAAAAAQAAAAAAAAAAP838SL4RI3j#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAABAAAAAQA#####wABZgAEMStyMQAAAAYAAAAAAT#wAAAAAAAAAAAABwAAAAUAAAAEAP####8AAmYxAANmPTEAAAAGCAAAAAcAAAAGAAAAAT#wAAAAAAAAAAAABAD#####AAJmMgADZj0yAAAABggAAAAHAAAABgAAAAFAAAAAAAAAAAAAAAQA#####wACZjMAA2Y9MwAAAAYIAAAABwAAAAYAAAABQAgAAAAAAAAAAAAEAP####8AAmY0AANmPTQAAAAGCAAAAAcAAAAGAAAAAUAQAAAAAAAAAAAABAD#####AAJmNQADZj01AAAABggAAAAHAAAABgAAAAFAFAAAAAAAAAAAAAQA#####wACZjYAA2Y9NgAAAAYIAAAABwAAAAYAAAABQBgAAAAAAAAAAAAEAP####8AAmY3AANmPTcAAAAGCAAAAAcAAAAGAAAAAUAcAAAAAAAAAAAABAD#####AAJmOAADZj04AAAABggAAAAHAAAABgAAAAFAIAAAAAAAAAAAAAQA#####wACZjkAA2Y9OQAAAAYIAAAABwAAAAYAAAABQCIAAAAAAAAAAAAEAP####8AA2YxMAAEZj0xMAAAAAYIAAAABwAAAAYAAAABQCQAAAAAAAAAAAAEAP####8AA2YxMQAEZj0xMQAAAAYIAAAABwAAAAYAAAABQCYAAAAAAAAAAAAEAP####8AA2YxMgAEZj0xMgAAAAYIAAAABwAAAAYAAAABQCgAAAAAAAD#####AAAAAgAGQ0xhdGV4AP####8BAAAAAQAA#####xBAc8AAAAAAAMAEzMzMzM0AAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAIbXElme2YxfQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtBRn19Cn0KewpcSWZ7ZjJ9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JEfX0KfQp7ClxJZntmM30Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17RkJ9fQp9CnsKXElme2Y0fQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtFQn19Cn0KewpcSWZ7ZjV9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0FFfX0KfQp7ClxJZntmNn0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0d9fQp9CnsKXElme2Y3fQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtJQX19Cn0KewpcSWZ7Zjh9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0dDfX0KfQp7ClxJZntmOX0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17REd9fQp9CnsKXElme2YxMH0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17SEV9fQp9CnsKXElme2YxMX0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17SUh9fQp9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JcLEl9fQp9Cn0KfQp9Cn0KfQp9Cn0KfQp9Cn3#####AAAAAQAKQ1BvaW50QmFzZQD#####AQAAAAAOAAJPJwDAKAAAAAAAAAAAAAAAAAAAAAAFAAFAT4AAAAAAAEB0NmZmZmZm#####wAAAAEAFENEcm9pdGVEaXJlY3Rpb25GaXhlAP####8BAAAAABAAAAEAAAABAAAAFAE#8AAAAAAAAP####8AAAABAA9DUG9pbnRMaWVEcm9pdGUA#####wEAAAAADgACSScAwBgAAAAAAAAAAAAAAAAAAAAABQABQEDvXCj1wo8AAAAV#####wAAAAEACUNEcm9pdGVBQgD#####AQAAAAAQAAABAAAAAQAAABQAAAAW#####wAAAAEAFkNEcm9pdGVQZXJwZW5kaWN1bGFpcmUA#####wEAAAAAEAAAAQAAAAEAAAAUAAAAF#####8AAAABAAlDQ2VyY2xlT0EA#####wEAAAAAAAABAAAAFAAAABb#####AAAAAQAQQ0ludERyb2l0ZUNlcmNsZQD#####AAAAGAAAABn#####AAAAAQAQQ1BvaW50TGllQmlwb2ludAD#####AQAAAAAQAAABAAAFAAEAAAAaAAAAEAD#####AQAAAAAOAAJKJwDAKAAAAAAAAMAQAAAAAAAAAAAFAAIAAAAa#####wAAAAIAB0NSZXBlcmUA#####wDm5uYAAAABAAAAFAAAABYAAAAcAAAAAAAAAQAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAT#wAAAAAAAAAAAAAT#wAAAAAAAA#####wAAAAEACkNVbml0ZXhSZXAA#####wAEdW5pdAAAAB3#####AAAAAQALQ0hvbW90aGV0aWUA#####wAAABQAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAAe#####wAAAAEAC0NQb2ludEltYWdlAP####8BAAAAABAAAlciAQAAAQAAAAAWAAAAH#####8AAAABAAlDTG9uZ3VldXIA#####wAAABQAAAAgAAAACQD#####AAAAAAAQAAFBAMAcAAAAAAAAQAgAAAAAAAAAAAUAAUBZwAAAAAAAQHFGZmZmZmYAAAAKAP####8BAAAAARAAAAEAAAABAAAAIgE#8AAAAAAAAAAAAAsA#####wAAAAAAEAABQgAAAAAAAAAAAEAIAAAAAAAAAAAFAAFAV8AAAAAAAAAAACMAAAAOAP####8BAAAAAAAAAQAAACIAAAAkAAAADgD#####AQAAAAAAAAEAAAAkAAAAIv####8AAAABABBDSW50Q2VyY2xlQ2VyY2xlAP####8AAAAlAAAAJgAAABAA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAQAAACcAAAAQAP####8AAAAAABAAAU8AwBgAAAAAAABAGAAAAAAAAAAABQACAAAAJ#####8AAAABAAlDUm90YXRpb24A#####wAAACkAAAAGAwAAAAcAAAAAAAAAAUAIAAAAAAAAAAAAFAD#####AAAAAAAOAAFDAEAgAAAAAAAAwCgAAAAAAAAAAAUAAAAAJAAAACoAAAAUAP####8AAAAAAA4AAUQAwBAAAAAAAADANwAAAAAAAAAABQAAAAArAAAAKgAAABQA#####wAAAAAADgABRQDAIAAAAAAAAMA1AAAAAAAAAAAFAAAAACwAAAAqAAAAFAD#####AAAAAAAOAAFGAMAzAAAAAAAAwCIAAAAAAAAAAAUAAAAALQAAACr#####AAAAAQAIQ1NlZ21lbnQA#####wAAAAAAEAAAAQAAAAEAAAAiAAAAJAAAABgA#####wAAAAAAEAAAAQAAAAEAAAAkAAAAKwAAABgA#####wAAAAAAEAAAAQAAAAEAAAArAAAALAAAABgA#####wAAAAAAEAAAAQAAAAEAAAAsAAAALQAAABgA#####wAAAAAAEAAAAQAAAAEAAAAtAAAALgAAABgA#####wAAAAAAEAAAAQAAAAEAAAAuAAAAIgAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAAIgAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAAJAAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAAKwAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAALAAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAALQAAABgA#####wAAAAAAEAAAAQAAAAEAAAApAAAALv####8AAAABAA5DTWFycXVlU2VnbWVudAD#####AAAA#wAAAAIAAAAAMwAAABkA#####wAAAP8AAAACAAAAADQAAAAZAP####8AAAD#AAAAAgAAAAAvAAAAGQD#####AAAA#wAAAAIAAAAAMAAAABkA#####wAAAP8AAAACAAAAADEAAAAZAP####8AAAD#AAAAAgAAAAAyAAAAGQD#####AAAA#wAAAAIAAAAANQAAABkA#####wAAAP8AAAACAAAAADYAAAAZAP####8AAAD#AAAAAgAAAAA3AAAAGQD#####AAAA#wAAAAIAAAAAOAAAABkA#####wAAAP8AAAACAAAAADkAAAAZAP####8AAAD#AAAAAgAAAAA6#####wAAAAIADUNNZXN1cmVBZmZpeGUA#####wABTwAAAB0AAAApAAAAGgD#####AAFBAAAAHQAAACIAAAAaAP####8AAUIAAAAdAAAAJAAAABoA#####wABQwAAAB0AAAArAAAAGgD#####AAFEAAAAHQAAACwAAAAaAP####8AAUUAAAAdAAAALQAAABoA#####wABRgAAAB0AAAAu#####wAAAAEAEUNTeW1ldHJpZUNlbnRyYWxlAP####8AAAArAAAAFAD#####AAAAAAAQAAFIAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALAAAAE4AAAAbAP####8AAAAuAAAAFAD#####AAAAAAAQAAFHAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALQAAAFAAAAAYAP####8AAAAAABAAAAEAAAABAAAALgAAAFEAAAAYAP####8AAAAAABAAAAEAAAABAAAAUQAAACIAAAAYAP####8AAAAAABAAAAEAAAABAAAAJAAAAE8AAAAYAP####8AAAAAABAAAAEAAAABAAAATwAAACsAAAAbAP####8AAAAsAAAAFAD#####AAAAAAAQAAFJAMAIAAAAAAAAwDgAAAAAAAAAAAUAAAAAKwAAAFYAAAAYAP####8AAAAAABAAAAEAAAABAAAALQAAAFcAAAAYAP####8AAAAAABAAAAEAAAABAAAAVwAAACwAAAAZAP####8AAAD#AAAAAgAAAABSAAAAGQD#####AAAA#wAAAAIAAAAAUwAAABkA#####wAAAP8AAAACAAAAAFQAAAAZAP####8AAAD#AAAAAgAAAABVAAAAGQD#####AAAA#wAAAAIAAAAAWQAAABkA#####wAAAP8AAAACAAAAAFgAAAAaAP####8AAUcAAAAdAAAAUQAAABoA#####wABSAAAAB0AAABPAAAAGgD#####AAFJAAAAHQAAAFf#####AAAAAQAIQ1ZlY3RldXIA#####wD#AAAAEAAAAQAAAAIAAAApAAAAKwD#####AAAAAQAHQ01pbGlldQD#####Af8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAApAAAAKwAAAAgA#####wD#AAAAQBwAAAAAAAA#8AAAAAAAAAAAAAAAZBQAAAAAAAEAAAAAAAAAAQAAAAAAAAAAAAdcdmVje2l9AAAAHAD#####AAB#AAAQAAABAAAAAgAAACkAAAAsAAAAAB0A#####wEAfwAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAKQAAACwAAAAIAP####8AAH8AAMAiAAAAAAAAP#AAAAAAAAAAAAAAAGcUAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAHXHZlY3tqfQAAAAMA#####wACaScAA0MtTwAAAAYB#####wAAAAEAF0NSZXN1bHRhdFZhbGV1ckNvbXBsZXhlAAAASgAAAB4AAABHAAAAAwD#####AAFqAANELU8AAAAGAQAAAB4AAABLAAAAHgAAAEcAAAADAP####8AA3JlcAABMAAAAAEAAAAAAAAAAAAAAAMA#####wAEc29sMQAFLWknK2oAAAAGAP####8AAAABAAxDTW9pbnNVbmFpcmUAAAAeAAAAaQAAAB4AAABqAAAAAwD#####AARzb2wyAActaScrMipqAAAABgAAAAAfAAAAHgAAAGkAAAAGAgAAAAFAAAAAAAAAAAAAAB4AAABqAAAAAwD#####AARzb2wzAAYyKmknLWoAAAAGAQAAAAYCAAAAAUAAAAAAAAAAAAAAHgAAAGkAAAAeAAAAagAAAAMA#####wAEc29sNAAIMippJy0yKmoAAAAGAQAAAAYCAAAAAUAAAAAAAAAAAAAAHgAAAGkAAAAGAgAAAAFAAAAAAAAAAAAAAB4AAABqAAAAAwD#####AARzb2w1AActaScrMipqAAAABgAAAAAfAAAAHgAAAGkAAAAGAgAAAAFAAAAAAAAAAAAAAB4AAABqAAAAAwD#####AARzb2w2AAUtaSctagAAAAYBAAAAHwAAAB4AAABpAAAAHgAAAGoAAAADAP####8ABHNvbDcABmknLTMqagAAAAYBAAAAHgAAAGkAAAAGAgAAAAFACAAAAAAAAAAAAB4AAABqAAAAAwD#####AARzb2w4AAYyKmknK2oAAAAGAAAAAAYCAAAAAUAAAAAAAAAAAAAAHgAAAGkAAAAeAAAAagAAAAMA#####wAEc29sOQAHLWknLTIqagAAAAYBAAAAHwAAAB4AAABpAAAABgIAAAABQAAAAAAAAAAAAAAeAAAAagAAAAMA#####wAFc29sMTAACS0zKmknKzIqagAAAAYAAAAAHwAAAAYCAAAAAUAIAAAAAAAAAAAAHgAAAGkAAAAGAgAAAAFAAAAAAAAAAAAAAB4AAABqAAAAAwD#####AAVzb2wxMQAIMyppJy0zKmoAAAAGAQAAAAYCAAAAAUAIAAAAAAAAAAAAHgAAAGkAAAAGAgAAAAFACAAAAAAAAAAAAB4AAABqAAAAAwD#####AAVzb2wxMgAJLTIqaScrMypqAAAABgAAAAAfAAAABgIAAAABQAAAAAAAAAAAAAAeAAAAaQAAAAYCAAAAAUAIAAAAAAAAAAAAHgAAAGr#####AAAAAwAQQ1Rlc3RFcXVpdmFsZW5jZQD#####AAR0ZXExAAAAbAAAAGsBAQAAAAE#8AAAAAAAAAEAAAAgAP####8ABHRlcTIAAABtAAAAawEBAAAAAT#wAAAAAAAAAQAAACAA#####wAEdGVxMwAAAG4AAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAR0ZXE0AAAAbwAAAGsBAQAAAAE#8AAAAAAAAAEAAAAgAP####8ABHRlcTUAAABwAAAAawEBAAAAAT#wAAAAAAAAAQAAACAA#####wAEdGVxNgAAAHEAAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAR0ZXE3AAAAcgAAAGsBAQAAAAE#8AAAAAAAAAEAAAAgAP####8ABHRlcTgAAABzAAAAawEBAAAAAT#wAAAAAAAAAQAAACAA#####wAEdGVxOQAAAHQAAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAV0ZXExMAAAAHUAAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAV0ZXExMQAAAHYAAABrAQEAAAABP#AAAAAAAAABAAAAIAD#####AAV0ZXExMgAAAHcAAABrAQEAAAABP#AAAAAAAAABAAAABAD#####AAZyZXNvbHUAjXNpKGYxLHRlcTEsc2koZjIsdGVxMixzaShmMyx0ZXEzLHNpKGY0LHRlcTQsc2koZjUsdGVxNSxzaShmNix0ZXE2LHNpKGY3LHRlcTcsc2koZjgsdGVxOCxzaShmOSx0ZXE5LHNpKGYxMCx0ZXExMCxzaShmMTEsdGVxMTEsdGVxMTIpKSkpKSkpKSkpKf####8AAAABAA1DRm9uY3Rpb24zVmFyAAAAAAcAAAAHAAAABwAAAHgAAAAhAAAAAAcAAAAIAAAABwAAAHkAAAAhAAAAAAcAAAAJAAAABwAAAHoAAAAhAAAAAAcAAAAKAAAABwAAAHsAAAAhAAAAAAcAAAALAAAABwAAAHwAAAAhAAAAAAcAAAAMAAAABwAAAH0AAAAhAAAAAAcAAAANAAAABwAAAH4AAAAhAAAAAAcAAAAOAAAABwAAAH8AAAAhAAAAAAcAAAAPAAAABwAAAIAAAAAhAAAAAAcAAAAQAAAABwAAAIEAAAAhAAAAAAcAAAARAAAABwAAAIIAAAAHAAAAg#####8AAAABAA1DRm9uY0NvbXBsZXhlAP####8ABHplcm8AEmFicyh6KTwwLjAwMDAwMDAwMQAAAAYEAAAABUD#####AAAAAgARQ1ZhcmlhYmxlRm9ybWVsbGUAAAAAAAAAAT4RLgvoJtaVAAF6AAAAAwD#####AAV0ZXN0MQAOemVybyhyZXAtc29sMSn#####AAAAAQAWQ0FwcGVsRm9uY3Rpb25Db21wbGV4ZQAAAIUAAAAGAQAAAB4AAABrAAAAHgAAAGwAAAADAP####8ABXRlc3QyAA56ZXJvKHJlcC1zb2wyKQAAACQAAACFAAAABgEAAAAeAAAAawAAAB4AAABtAAAAAwD#####AAV0ZXN0MwAOemVybyhyZXAtc29sMykAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAbgAAAAMA#####wAFdGVzdDQADnplcm8ocmVwLXNvbDQpAAAAJAAAAIUAAAAGAQAAAB4AAABrAAAAHgAAAG8AAAADAP####8ABXRlc3Q1AA56ZXJvKHJlcC1zb2w1KQAAACQAAACFAAAABgEAAAAeAAAAawAAAB4AAABwAAAAAwD#####AAV0ZXN0NgAOemVybyhyZXAtc29sNikAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAcQAAAAMA#####wAFdGVzdDcADnplcm8ocmVwLXNvbDcpAAAAJAAAAIUAAAAGAQAAAB4AAABrAAAAHgAAAHIAAAADAP####8ABXRlc3Q4AA56ZXJvKHJlcC1zb2w4KQAAACQAAACFAAAABgEAAAAeAAAAawAAAB4AAABzAAAAAwD#####AAV0ZXN0OQAOemVybyhyZXAtc29sOSkAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAdAAAAAMA#####wAGdGVzdDEwAA96ZXJvKHJlcC1zb2wxMCkAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAdQAAAAMA#####wAGdGVzdDExAA96ZXJvKHJlcC1zb2wxMSkAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAdgAAAAMA#####wAGdGVzdDEyAA96ZXJvKHJlcC1zb2wxMikAAAAkAAAAhQAAAAYBAAAAHgAAAGsAAAAeAAAAd#####8AAAABAA1DUGFydGllUmVlbGxlAP####8ABmV4YWN0MQAAAIYAAAAlAP####8ABmV4YWN0MgAAAIcAAAAlAP####8ABmV4YWN0MwAAAIgAAAAlAP####8ABmV4YWN0NAAAAIkAAAAlAP####8ABmV4YWN0NQAAAIoAAAAlAP####8ABmV4YWN0NgAAAIsAAAAlAP####8ABmV4YWN0NwAAAIwAAAAlAP####8ABmV4YWN0OAAAAI0AAAAlAP####8ABmV4YWN0OQAAAI4AAAAlAP####8AB2V4YWN0MTAAAACPAAAAJQD#####AAdleGFjdDExAAAAkAAAACUA#####wAHZXhhY3QxMgAAAJEAAAAEAP####8ABWV4YWN0AKVzaShmMSxleGFjdDEsc2koZjIsZXhhY3QyLHNpKGYzLGV4YWN0MyxzaShmNCxleGFjdDQsc2koZjUsZXhhY3Q1LHNpKGY2LGV4YWN0NixzaShmNyxleGFjdDcsc2koZjgsZXhhY3Q4LHNpKGY5LGV4YWN0OSxzaShmMTAsZXhhY3QxMCxzaShmMTEsZXhhY3QxMSxleGFjdDEyKSkpKSkpKSkpKSkAAAAhAAAAAAcAAAAHAAAABwAAAJIAAAAhAAAAAAcAAAAIAAAABwAAAJMAAAAhAAAAAAcAAAAJAAAABwAAAJQAAAAhAAAAAAcAAAAKAAAABwAAAJUAAAAhAAAAAAcAAAALAAAABwAAAJYAAAAhAAAAAAcAAAAMAAAABwAAAJcAAAAhAAAAAAcAAAANAAAABwAAAJgAAAAhAAAAAAcAAAAOAAAABwAAAJkAAAAhAAAAAAcAAAAPAAAABwAAAJoAAAAhAAAAAAcAAAAQAAAABwAAAJsAAAAhAAAAAAcAAAARAAAABwAAAJwAAAAHAAAAnQAAAAQA#####wAHcmVwb25zZQAac2kocmVzb2x1LDEsc2koZXhhY3QsMiwwKSkAAAAhAAAAAAcAAACEAAAAAT#wAAAAAAAAAAAAIQAAAAAHAAAAngAAAAFAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAgA#####wEAAAABAAVwb2ludP####8QQHPgAAAAAABAcEZmZmZmZgAAAAAAAAAAAAAAAAABAAAAAAAAAAAAI1x0ZXh0e08vL0EvL0IvL0MvL0QvL0UvL0YvL0cvL0gvL0l9AAAACAD#####AQAAAAEAAP####8QQHQQAAAAAABAceZmZmZmZgAAAAAAAAAAAAAAAAABAAAAAAAAAAAAC1x0ZXh0e2kvL2p9AAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAAAgAAAAUAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACQAAACiAAAAHAD#####AP8A#wAQAAABAAAAAgAAAKMAAAAsAAAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAAJAAAAFAD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAuAAAApQAAABwA#####wD#AP8AEAAAAQAAAAIAAACmAAAAJAAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAHAAAACgAAABQA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALQAAAKgAAAAcAP####8A#wD#ABAAAAEAAAACAAAAqQAAACQAAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAAAsAAAAUAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAC0AAACrAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAAAwAAAAUAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFEAAACtAAAAHAD#####AP8A#wAQAAABAAAAAgAAACkAAACuAAAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAANAAAAFAD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABXAAAAsAAAABwA#####wD#AP8AEAAAAQAAAAIAAACxAAAAIgAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAHAAAADgAAABQA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAUQAAALMAAAAcAP####8A#wD#ABAAAAEAAAACAAAAtAAAACsAAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABwAAAA8AAAAUAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACwAAAC2AAAAHAD#####AP8A#wAQAAABAAAAAgAAALcAAABRAAAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAAQAAAAFAD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABPAAAAuQAAABwA#####wD#AP8AEAAAAQAAAAIAAAC6AAAALQAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAHAAAAEQAAABQA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAATwAAALwAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAHAAAAEgAAABQA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAJAAAAL4AAAAcAP####8A#wD#ABAAAAEAAAACAAAAvwAAAFcAAAAACAD#####AQAA#wEAAP####8SQHPwAAAAAABARTMzMzMzMwEB7+#7AAAAAAAAAAAAAAABAAAAAAAAAAAK4lxiZWdpbnthcnJheX17bH0KXElme2YxfQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtBRn19PVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtBR319K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHRn19PS1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0N9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fQpcXFx0ZXh0e2RvbmMgfVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtBRn19PS1cdmVje2l9K1x2ZWN7an0KfQp7ClxJZntmMn0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QkR9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QkF9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QUR9fT0tXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17QkR9fT0tXHZlY3tpfSsyXHZlY3tqfQp9CnsKXElme2YzfQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtGQn19PVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtGR319K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHQn19PS1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fSsyXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17RkJ9fT0yXHZlY3tpfS1cdmVje2p9Cn0KewpcSWZ7ZjR9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0VCfX09XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0VHfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0dCfX09LTJcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fSsyXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17RUJ9fT0yXHZlY3tpfS0yXHZlY3tqfQp9CnsKXElme2Y1fQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtBRX19PVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtBR319K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHRX19PS1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0N9fSsyXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17RUJ9fT0tXHZlY3tpfSsyXHZlY3tqfQp9CnsKXElme2Y2fQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPR319PVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPQX19K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtBR319PS1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fS1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0N9fQpcXFx0ZXh0e2RvbmMgfVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPR319PS1cdmVje2l9LVx2ZWN7an0KfQp7ClxJZntmN30Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17SUF9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17SUd9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17R0F9fT0tM1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPRH19K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPQ319ClxcXHRleHR7ZG9uYyB9XG92ZXJyaWdodGFycm93IHtcbWF0aHJte09HfX09XHZlY3tpfS0zXHZlY3tqfQp9CnsKXElme2Y4fQp7ClxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHQ319PVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHQn19K1xvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtCQ319PTJcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0N9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fQpcXFx0ZXh0e2RvbmMgfVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtHQ319PTJcdmVje2l9K1x2ZWN7an0KfQp7ClxJZntmOX0Kewpcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17REd9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17REV9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17RUd9fT0tXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0tMlxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPRH19ClxcXHRleHR7ZG9uYyB9XG92ZXJyaWdodGFycm93IHtcbWF0aHJte09HfX09LVx2ZWN7aX0tMlx2ZWN7an0KfQp7ClxJZntmMTB9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0hFfX09XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0hHfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0dFfX09LTNcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0N9fSsyXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09EfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17SEV9fT0tM1x2ZWN7aX0rMlx2ZWN7an0KfQp7ClxJZntmMTF9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0lIfX09XG92ZXJyaWdodGFycm93IHtcbWF0aHJte0lHfX0rXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0dIfX09LTNcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fSszXG92ZXJyaWdodGFycm93IHtcbWF0aHJte09DfX0KXFxcdGV4dHtkb25jIH1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17SUh9fT0zXHZlY3tpfS0zXHZlY3tqfQp9CnsKXG92ZXJyaWdodGFycm93IHtcbWF0aHJte0JcLEl9fT1cb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17Qkd9fStcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17R0l9fT0tMlxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtPRH19KzNcb3ZlcnJpZ2h0YXJyb3cge1xtYXRocm17T0R9fQpcXFx0ZXh0e2RvbmMgfVxvdmVycmlnaHRhcnJvdyB7XG1hdGhybXtCXCxJfX09LTJcdmVje2l9KzNcdmVje2p9Cn0gCn0gCn0gCn0gCn0gCn0gCn0gCn0gCn0gCn0gCn0gClxlbmR7YXJyYXl9AAAAHAD#####AP8A#wAQAAABAAAAAgAAACIAAACsAAAAABwA#####wD#AP8AEAAAAQAAAAIAAABXAAAAvQD#####AAAAAQAQQ01hY3JvQXBwYXJpdGlvbgD#####AQAA#wEAAP####8QQHPwAAAAAABAZUzMzMzMzQIB9vr+AAAAAAAAAAAAAAABAAAAAAAAAAAADXZvaXIgc29sdXRpb24AAAAAAAEAAADBAAAAABMA#####wAAACkAAAAGAwAAAAE#8AAAAAAAAAAAAAcAAAAHAAAAFAD#####AP8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAiAAAAxQAAABwA#####wD#AP8AEAAAAQAAAAIAAADGAAAALgAAAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAAcAAAAUAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFEAAADIAAAAHAD#####AH8AAAAQAAABAAAAAgAAAMYAAADJAAAAABwA#####wAAf38AEAAAAQAAAAIAAADJAAAALgAAAAAdAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAMYAAADJAAAACAD#####AH8AAAEAAAAAAMwSAAAAAAABAAAAAAAAAAEAAAAAAAAAAAAILVx2ZWN7aX0AAAAdAP####8AAH9#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAMkAAAAuAAAACAD#####AAB#fwDAIAAAAAAAAEAIAAAAAAAAAAAAAADOEgAAAAAAAgAAAAIAAAABAAAAAAAAAAAAB1x2ZWN7an0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAAgAAAAUAP####8AfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACIAAADQAAAAHQD#####AH8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAkAAAA0QAAAAgA#####wB#AAABAAAAAADSEgAAAAAAAQAAAAAAAAABAAAAAAAAAAAACC1cdmVje2l9AAAADQD#####AQB#AAAQAAABAAAAAgAAANEAAAA1AAAACwD#####AQB#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABP7EO2tMCJbsAAADU#####wAAAAEADENUcmFuc2xhdGlvbgD#####AAAA0QAAACwAAAAUAP####8BAH8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAANUAAADWAAAAHAD#####AAD#AAAQAAABAAAAAgAAANUAAADXAAAAAB0A#####wAA##8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAA1QAAANcAAAAIAP####8AAP8AAMAYAAAAAAAAP#AAAAAAAAAAAAAAANkQAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAIMlx2ZWN7an0AAAAcAP####8AfwAAABAAAAEAAAACAAAAJAAAANEAAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABgoAAAAHAAAAAQAAAAcAAAAJAAAAFAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABRAAAA3AAAAB0A#####wEAfwAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALgAAAN0AAAAcAP####8AAP8AABAAAAEAAAACAAAALgAAAN0AAAAACAD#####AAD#AADAFAAAAAAAAMAQAAAAAAAAAAAAAADeEAAAAAAAAgAAAAIAAAABAAAAAAAAAAAACC1cdmVje2p9AAAAHAD#####AH8AAAAQAAABAAAAAgAAAN0AAAAkAAAAAB0A#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAA3QAAACQAAAAIAP####8AfwAAAEAkAAAAAAAAwBgAAAAAAAAAAAAAAOISAAH2+v4AAAABAAAAAgAAAAEAAAAAAAAAAAAIMlx2ZWN7aX0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAAoAAAAUAP####8BfwB#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFEAAADkAAAAHQD#####AX8AfwAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAkAAAA5QAAAAgA#####wB#AH8AQDMAAAAAAAC#8AAAAAAAAAAAAAAA5hIAAAAAAAEAAAAAAAAAAQAAAAAAAAAAAAgyXHZlY3tpfQAAABwA#####wB#AH8AEAAAAQAAAAIAAADlAAAAJAAAAAAdAP####8BAP8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAC0AAADlAAAAHAD#####AAD#AAAQAAABAAAAAgAAAC0AAADlAAAAAAgA#####wAA#wAAQAAAAAAAAADAEAAAAAAAAAAAAAAA6RIAAAAAAAIAAAACAAAAAQAAAAAAAAAAAAktMlx2ZWN7an0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAAsAAAAUAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFEAAADsAAAAHQD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAiAAAA7QAAABwA#####wB#AAAAEAAAAQAAAAIAAAAiAAAA7QAAAAAIAP####8AfwAAAQAAAAAA7hIAAAAAAAEAAAAAAAAAAQAAAAAAAAAAAAgtXHZlY3tpfQAAAB0A#####wEA#wAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAA7QAAAC0AAAAcAP####8AAP8AABAAAAEAAAACAAAA7QAAAC0AAAAACAD#####AAD#AAC#8AAAAAAAAMAYAAAAAAAAAAAAAADxEAAAAAAAAgAAAAIAAAABAAAAAAAAAAAACDJcdmVje2p9AAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABgoAAAAHAAAAAQAAAAcAAAAMAAAAFAD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAiAAAA9AAAAB0A#####wEA#wAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAKQAAAPUAAAAcAP####8AAP8AABAAAAEAAAACAAAAKQAAAPUAAAAACAD#####AAD#AAEAAAAAAPYSAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAILVx2ZWN7an0AAAAdAP####8BfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAPUAAABRAAAAHAD#####AH8AAAAQAAABAAAAAgAAAPUAAABRAAAAAAgA#####wB#AAABAAAAAAD5EgAAAAAAAQAAAAAAAAABAAAAAAAAAAAACC1cdmVje2l9AAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABgoAAAAHAAAAAQAAAAcAAAANAAAAFAD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABRAAAA#AAAAB0A#####wEA#wAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAVwAAAP0AAAAcAP####8AAP8AABAAAAEAAAACAAAAVwAAAP0AAAAACAD#####AAD#AADAAAAAAAAAAMAQAAAAAAAAAAAAAAD+EgAAAAAAAgAAAAIAAAABAAAAAAAAAAAACS0zXHZlY3tqfQAAAB0A#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAA#QAAACIAAAAcAP####8AfwAAABAAAAEAAAACAAAA#QAAACIAAAAACAD#####AH8AAADACAAAAAAAAEAIAAAAAAAAAAAAAAEBEgAAAAAAAQAAAAAAAAABAAAAAAAAAAAAB1x2ZWN7aX0AAAATAP####8AAAApAAAABgMAAAABP#AAAAAAAAAAAAAGCgAAAAcAAAABAAAABwAAAA4AAAAUAP####8AfwAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAACQAAAEEAAAAHQD#####AH8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABRAAABBQAAABwA#####wB#AAAAEAAAAQAAAAIAAABRAAABBQAAAAAIAP####8AfwAAAEAYAAAAAAAAAAAAAAAAAAAAAAAAAQYSAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAIMlx2ZWN7aX0AAAAdAP####8AAH8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAQUAAAArAAAAHAD#####AAB#AAAQAAABAAAAAgAAAQUAAAArAAAAAAgA#####wAAfwAAQBQAAAAAAADACAAAAAAAAAAAAAABCRAAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAdcdmVje2p9AAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABgoAAAAHAAAAAQAAAAcAAAAPAAAAFAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAAtAAABDAAAAB0A#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALAAAAQ0AAAAcAP####8AfwAAABAAAAEAAAACAAAALAAAAQ0AAAAACAD#####AH8AAADAEAAAAAAAAMAQAAAAAAAAAAAAAAEOEgAAAAAAAQAAAAIAAAABAAAAAAAAAAAACC1cdmVje2l9AAAAHQD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAENAAAAUQAAABwA#####wAA#wAAEAAAAQAAAAIAAAENAAAAUQAAAAAIAP####8AAP8AAAAAAAAAAAAAwBgAAAAAAAAAAAAAARESAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAJLTJcdmVje2p9AAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABgoAAAAHAAAAAQAAAAcAAAAQAAAAFAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABRAAABFAAAAB0A#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAATwAAARUAAAAcAP####8AfwAAABAAAAEAAAACAAAATwAAARUAAAAACAD#####AH8AAAAAAAAAAAAAAD#wAAAAAAAAAAAAAAEWEAAAAAAAAQAAAAAAAAABAAAAAAAAAAAACS0zXHZlY3tpfQAAAB0A#####wEA#wAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAABFQAAAC0AAAAIAP####8AAP8AAMAAAAAAAAAAwBgAAAAAAAAAAAAAARkSAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAIMlx2ZWN7an0AAAAcAP####8AAP8AABAAAAEAAAACAAABFQAAAC0AAAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABgoAAAAHAAAAAQAAAAcAAAARAAAAFAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABRAAABHAAAAB0A#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAABHQAAAE8AAAAIAP####8AfwAAAL#wAAAAAAAAQAAAAAAAAAAAAAAAAR4SAAAAAAABAAAAAAAAAAEAAAAAAAAAAAAIM1x2ZWN7aX0AAAAcAP####8AfwAAABAAAAEAAAACAAABHQAAAE8AAAAAHQD#####AQD#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABXAAABHQAAABwA#####wAA#wAAEAAAAQAAAAIAAABXAAABHQAAAAAIAP####8AAP8AAMAUAAAAAAAAwAgAAAAAAAAAAAAAASESAAAAAAACAAAAAgAAAAEAAAAAAAAAAAAJLTNcdmVje2p9AAAAEwD#####AAAAKQAAAAYDAAAAAT#wAAAAAAAAAAAABgoAAAAHAAAAAQAAAAcAAAASAAAAFAD#####AX8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABRAAABJAAAAB0A#####wF#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAJAAAASUAAAAcAP####8AfwAAABAAAAEAAAACAAAAJAAAASUAAAAACAD#####AH8AAADARYAAAAAAAMAAAAAAAAAAAAAAAAEmEgAAAAAAAAAAAAAAAAABAAAAAAAAAAAACS0zXHZlY3tpfQAAAB0A#####wEA#wAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAABJQAAAFcAAAAcAP####8AAP8AABAAAAEAAAACAAABJQAAAFcAAAAACAD#####AAD#AADACAAAAAAAAMAIAAAAAAAAAAAAAAEpEgAAAAAAAgAAAAIAAAABAAAAAAAAAAAACDNcdmVje2p9#####wAAAAEAH0NNYWNyb0FmZmVjdGF0aW9uVmFsZXVyVmFyaWFibGUA#####wEAAP8BAAD#####EEBz8AAAAAAAQGtMzMzMzM0CAfb6#gAAAAAAAAAAAAAAAQAAAAAAAAAAAAdjb3IgPSAxAAAAAAABP#AAAAAAAAAAAAAB#####wAAAAEAEUNNYWNyb1N1aXRlTWFjcm9zAP####8BAAD#AQAA#####xBAfJAAAAAAAEBlbMzMzMzNAgH2+v4AAAAAAAAAAAAAAAEAAAAAAAAAAAAIc29sdXRpb24AAAAAAAIAAAEsAAAAxAAAACH##########w==
Pour l'ouvrir dans MathGraph32, utilisez l'icône ![]() de création d'une figure et choisissez Figure par code Base 64 et, dans la boîte de dialogue qui s'ouvre, collez le code Base 64 ci-dessus.
de création d'une figure et choisissez Figure par code Base 64 et, dans la boîte de dialogue qui s'ouvre, collez le code Base 64 ci-dessus.
A part la figure elle-même, certains éléments nt été cachés ou ne sont pas visibles.
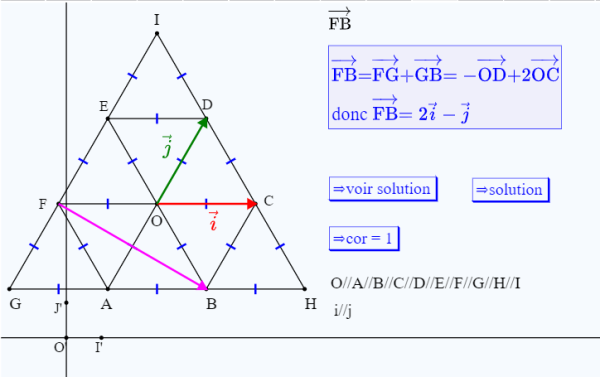
Voici ci-dessous un aperçu de la figure dans laquelle certains éléments ont été démasqués :
Pour créer les éléments géométriques de base de cette figure, on a d'abord utilisé l'icône ![]() puis choisi de créer une figure munie d'un repère en décochant les cases Quadrillage vertical et Quadrillage horizontal et en sélectionnant la case Sans graduation.
puis choisi de créer une figure munie d'un repère en décochant les cases Quadrillage vertical et Quadrillage horizontal et en sélectionnant la case Sans graduation.
Les points O, I et J définissant le repère ont ensuite été renommés en O', I' et J' puis avec l'outil on a masqué le point O', le point I', le point J' et les droites (O'I') et (O'J').
Le point A a ensuite été créé comme un point libre. Nous ne détaillerons pas la façon de créer les points B, C, D, E, F, G, H, I et O assez classique. La figure a ensuite été enrichie de segments et de marques de segments (que l'on crée avec l'outil ![]() et en cliquant sur le segment après avoir choisi une épaisseur de trait et une couleur).
et en cliquant sur le segment après avoir choisi une épaisseur de trait et une couleur).
Vous pouvez maintenant examiner comment a été créée cette figure en utilisant dans la barre supérieure l'outil ![]() protocole. En utilisant les touches haut et bas vous pouvez naviguer dans la figure pour voir les différents éléments de celle-ci.
protocole. En utilisant les touches haut et bas vous pouvez naviguer dans la figure pour voir les différents éléments de celle-ci.
Nous détaillerons ci-dessous les éléments de cette figure, à l'exception de ceux qui ont servi à la création de des éléments géométriques de base. Le calcul pi fait partie de toutes les figures et n'est pas modifiable (il ne s'agit bien sûr que d'une valeur approchée).
Suivent ensuite 12 calculs réels f1 à f12 qui servent plus tard dans les affichages LaTeX conditionnels.
Par exemple, le calcul f1 est défini par la formule f = 1 et prend comme valeur 1 si f est égal à 1 et 0 sinon.
Ensuite arrivent dans le protocole un affichage LaTeX libre indiqué dans le protocole par lat1: Affichage LaTeX
Cet affichage LaTeX a été crée avec l'outil ![]() et est récupéré par la ressource pour compléter la consigne (voir plus loin dans la paramétrage de la ressource).
et est récupéré par la ressource pour compléter la consigne (voir plus loin dans la paramétrage de la ressource).
Il est important que cet affichage LaTeX soit le premier affichage LaTeX de la figure. Si ce n'était pas le cas il faudrait le reclasser.
Voici le code LaTeX de cet affichage qui utilise des affichages LaTeX conditionnels :
\If{f1}
{
\overrightarrow {\mathrm{AF}}
}
{
\If{f2}
{
\overrightarrow {\mathrm{BD}}
}
{
\If{f3}
{
\overrightarrow {\mathrm{FB}}
}
{
\If{f4}
{
\overrightarrow {\mathrm{EB}}
}
{
\If{f5}
{
\overrightarrow {\mathrm{AE}}
}
{
\If{f6}
{
\overrightarrow {\mathrm{OG}}
}
{
\If{f7}
{
\overrightarrow {\mathrm{IA}}
}
{
\If{f8}
{
\overrightarrow {\mathrm{GC}}
}
{
\If{f9}
{
\overrightarrow {\mathrm{DG}}
}
{
\If{f10}
{
\overrightarrow {\mathrm{HE}}
}
{
\If{f11}
{
\overrightarrow {\mathrm{IH}}
}
{
\overrightarrow {\mathrm{B\,I}}
}
}
}
}
}
}
}
}
}
}
}
Ainsi si, par exemple, f est égal à 1, le code LaTeX renvoyé sera : \overrightarrow {\mathrm{AF}}.
Dans la consigne, les caractères $£a£ seront alors remplacés par ce code LaTeX.
Détaillons la nature et l'objet de certains des éléments suivants de la igure visibles dans le protocole.
Ont ensuite été créés 10 mesures d'affixes des points O, A, B, C, D, E, F, G, H, I des points ayant les mêmes noms.
Pour créer par exemple la première on a utilisé l'outil ![]() situé dans la barre d'outils de créations de calculs, on a ensuite cliqué sur le point O. Une boîte de dialogue s'est ouverte. Le seul repère de la figure étant sélectionné par défaut, il suffit ensuite d'entre le nom de la mesure, ici O, et de valider la boîte de dialogue.
situé dans la barre d'outils de créations de calculs, on a ensuite cliqué sur le point O. Une boîte de dialogue s'est ouverte. Le seul repère de la figure étant sélectionné par défaut, il suffit ensuite d'entre le nom de la mesure, ici O, et de valider la boîte de dialogue.
Cas mesures complexes nous serviront pas la suite à valider la réponse de l'élève.
Ensuite ont été crées les calculs complexes suivants avec l'outil ![]() de création d'un calcul complexe.
de création d'un calcul complexe.
| Nom du calcul complexe | Formule | Commentaire |
|---|---|---|
| i' | C-O | Les résultats finaux de l'élève devront être exprimés en fonction de i' et de j. A noter que ce calcul est nommé i' mais que dans sa réponse l'élève utilisera la lettre i pour le vecteur correspondant |
| j | D-O | |
| rep | 0 | Ce calcul contiendra la réponse entrée par l'élève |
| sol1 | -i'+j | Contient la réponse finale attendue de l'élève si f = 1 |
| sol2 | -i'+2*j | Contient la réponse finale attendue de l'élève si f = 2 |
| sol3 | 2*i'-j | Contient la réponse finale attendue de l'élève si f = 3 |
| sol4 | 2*i'-2*j | Contient la réponse finale attendue de l'élève si f = 4 |
| sol5 | -i'+2*j | Contient la réponse finale attendue de l'élève si f = 5 |
| sol6 | -i'-j | Contient la réponse finale attendue de l'élève si f = 6 |
| sol7 | i'-3*j | Contient la réponse finale attendue de l'élève si f = 7 |
| sol8 | 2*i'+j | Contient la réponse finale attendue de l'élève si f = 8 |
| sol9 | -i'-2*j | Contient la réponse finale attendue de l'élève si f = 9 |
| sol10 | -3*i'+2*j | Contient la réponse finale attendue de l'élève si f = 10 |
| sol11 | 3*i'-3*j | Contient la réponse finale attendue de l'élève si f = 11 |
| sol12 | -2*i'+3*j | Contient la réponse finale attendue de l'élève si f = 12 |
Ensuite ont été créés 12 tests d'équivalences entre les calculs précédents et le calcul complexe rep. Ces tests ont pour nom teq1, teq2, …, teq12.
Pour cela il faut utiliser l'icône ![]() situé à droite de la barre de création de calculs quand elle est déroulée et choisir dans la liste Test d'équivalence.
situé à droite de la barre de création de calculs quand elle est déroulée et choisir dans la liste Test d'équivalence.
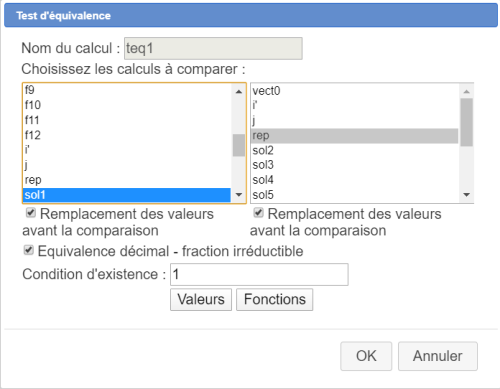
Voici par exemple comment a été crée le test d'équivalence nommé teq1 :
A noter qu'il faut cocher la case Remplacement des valeurs avant la comparaison à gauche et à droite. (Ainsi les valeurs des complexes A, B, C, D, E, F, G, H, I, O, i' et j seront remplacées avant de regarder si la réponse de l'élève contenue dans rep et le calcul solution sol1 sont des calculs équivalents.
Ensuite ont été créés les calculs ou fonctions suivants :
| Nom de l'objet | Nature | Formule | Commentaire |
|---|---|---|---|
| resolu | Calcul réel | si(f1,teq1,si(f2,teq2,si(f3,teq3,si(f4,teq4, si(f5,teq5,si(f6,teq6,si(f7,teq7,si(f8,teq8,si(f9,teq9, si(f10,teq10,si(f11,teq11,teq12))))))))))) | Renvoie 1 si la réponse de l'élève est équivalente à la réponse finale attendue et 0 sinon |
| zero | Fonction complexe de la variable z | abs(z)<0.000000001 | Renvoie le complexe 1 si le module de z est inférieur à 0.000000001 et 0 sinon |
| test1 | Calcul complexe | zero(rep-sol1) | Renvoie le complexe 1 si le module de la différence entre rep et sol1 est inférieur à 0.000000001 |
| … | |||
| test12 | Calcul complexe | zero(rep-sol12) | Renvoie le complexe 1 si le module de la différence entre rep et sol3 est inférieur à 0.000000001 |
Ensuite ont été créées 12 parties réelles de complexes nommées exact1 à exact12.
Pour créer une partie réelle de complexe, il faut utiliser l'icône ![]() situé à droite de la barre de création de calculs quand elle est déroulée et choisir dans la liste Partie réelle.
situé à droite de la barre de création de calculs quand elle est déroulée et choisir dans la liste Partie réelle.
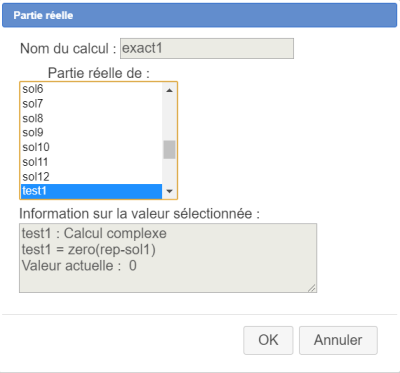
Voici par exemple la boîte de dialogue pour la création de exact1 :
Ensuite ont été créé les deux calculs réels suivants. Ce sont ces calculs qui vont indiquer sir la réponse de l'élève est bonne ou non, est bien la réponse finale attendue ou non.
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| exact | si(f1,exact1,si(f2,exact2,si(f3,exact3,si(f4,exact4, si(f5,exact5,si(f6,exact6,si(f7,exact7,si(f8,exact8, si(f9,exact9,si(f10,exact10,si(f11,exact11,exact12))))))))))) | Vaut 1 si la réponse de l'élève est exacte (à epsilon près |
| reponse | si(resolu,1,si(exact,2,0)) | C'est ce calcul valide la réponse de l'élève. Ce calcul renvoie 1 si la réponse de l'élève contenue dans rep est la réponse finale attendue, 2 si la réponse n'est pas finale mais est exacte et 0 sinon |