Table des matières
Résolution d'équation à solutions multiples
Notre but est créer dans LaboMep un exercice analogue à cet exercice.
On propose une équation à l'élève.
Il doit d'abord, à l'aide d'une liste déroulante, indiquer s'il y a ou non des solutions puis, s'il y en a, la résoudre.

Il peut résoudre progressivement. Par exemple si l'équation est 3x^3 - x = 0, il pourra entrer comme première proposition x(3x²-1) = 0. On lui dira alors que ce qu'il a proposé est vérifié par les solutions.
Il pourra ensuite par exemple entrer comme deuxième ligne de calcul x = 0; x² = 1/3 etc., le ; jouant le rôle d'un ou logique.

On considérera qu'il aura fini lorsqu'il entrera comme proposition : x = 0; x = √(3)/3; x = -√(3)/3 (dans cet ordre ou un ordre différent).
S'il propose x = 0; x = 1/√(3); x = -1/√(3) on lui dira que la résolution est bonne mais que le calcul n'est pas terminé.
Pour créer cette ressource vous pouvez utiliser MathGraph32 dans sa version en ligne.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
Etape 1 : Création de la figure MathGraph
Commencez par créer la figure mathgraph.
Si vous désirez sauter ce qui suit vous pouvez utiliser le code Base 64 de la figure ci-dessous et, dans MathGraph32, utiliser l'icône ![]() puis choisir Figure par code Base 64.
puis choisir Figure par code Base 64.
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAQPAAACjgAAAQEAAAAAAAAAAQAAAF7#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AAVuYnZhcgABMwAAAAFACAAAAAAAAAAAAAIA#####wAGbmJjYXMxAAE0AAAAAUAQAAAAAAAAAAAAAgD#####AAZuYmNhczIAATkAAAABQCIAAAAAAAAAAAACAP####8ABm5iY2FzMwABNQAAAAFAFAAAAAAAAAAAAAIA#####wACcjEAE2ludChyYW5kKDApKm5iY2FzMSn#####AAAAAgAJQ0ZvbmN0aW9uAv####8AAAABAApDT3BlcmF0aW9uAgAAAAMRAAAAAQAAAAAAAAAAP+jQJsbNXur#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAAAgAAAAIA#####wACcjIAE2ludChyYW5kKDApKm5iY2FzMikAAAADAgAAAAQCAAAAAxEAAAABAAAAAAAAAAA#5VzWO1hB+AAAAAUAAAADAAAAAgD#####AAJyMwATaW50KHJhbmQoMCkqbmJjYXMzKQAAAAMCAAAABAIAAAADEQAAAAEAAAAAAAAAAD+29yb1IS4AAAAABQAAAAQAAAACAP####8AAWYABDErcjEAAAAEAAAAAAE#8AAAAAAAAAAAAAUAAAAFAAAAAgD#####AAFhAAQxK3IyAAAABAAAAAABP#AAAAAAAAAAAAAFAAAABgAAAAIA#####wACYjEABHIzKzIAAAAEAAAAAAUAAAAHAAAAAUAAAAAAAAAAAAAAAgD#####AAJiMgAsKHIzPTApKjErKHIzPTEpKjMrKHIzPTIpKjUrKHIzPTMpKjcrKHIzPTQpKjkAAAAEAAAAAAQAAAAABAAAAAAEAAAAAAQCAAAABAgAAAAFAAAABwAAAAEAAAAAAAAAAAAAAAE#8AAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAE#8AAAAAAAAAAAAAFACAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFAAAAAAAAAAAAAAAFAFAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFACAAAAAAAAAAAAAFAHAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFAEAAAAAAAAAAAAAFAIgAAAAAAAAAAAAIA#####wACYjMALChyMz0wKSoxKyhyMz0xKSoyKyhyMz0yKSo0KyhyMz0zKSo1KyhyMz00KSo3AAAABAAAAAAEAAAAAAQAAAAABAAAAAAEAgAAAAQIAAAABQAAAAcAAAABAAAAAAAAAAAAAAABP#AAAAAAAAAAAAAEAgAAAAQIAAAABQAAAAcAAAABP#AAAAAAAAAAAAABQAAAAAAAAAAAAAAEAgAAAAQIAAAABQAAAAcAAAABQAAAAAAAAAAAAAABQBAAAAAAAAAAAAAEAgAAAAQIAAAABQAAAAcAAAABQAgAAAAAAAAAAAABQBQAAAAAAAAAAAAEAgAAAAQIAAAABQAAAAcAAAABQBAAAAAAAAAAAAABQBwAAAAAAAAAAAACAP####8AAmI0ACwocjM9MCkqMSsocjM9MSkqMysocjM9MikqNSsocjM9MykqNysocjM9NCkqOQAAAAQAAAAABAAAAAAEAAAAAAQAAAAABAIAAAAECAAAAAUAAAAHAAAAAQAAAAAAAAAAAAAAAT#wAAAAAAAAAAAABAIAAAAECAAAAAUAAAAHAAAAAT#wAAAAAAAAAAAAAUAIAAAAAAAAAAAABAIAAAAECAAAAAUAAAAHAAAAAUAAAAAAAAAAAAAAAUAUAAAAAAAAAAAABAIAAAAECAAAAAUAAAAHAAAAAUAIAAAAAAAAAAAAAUAcAAAAAAAAAAAABAIAAAAECAAAAAUAAAAHAAAAAUAQAAAAAAAAAAAAAUAiAAAAAAAAAAAAAgD#####AAJiNQAsKHIzPTApKjErKHIzPTEpKjIrKHIzPTIpKjMrKHIzPTMpKjQrKHIzPTQpKjYAAAAEAAAAAAQAAAAABAAAAAAEAAAAAAQCAAAABAgAAAAFAAAABwAAAAEAAAAAAAAAAAAAAAE#8AAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAE#8AAAAAAAAAAAAAFAAAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFAAAAAAAAAAAAAAAFACAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFACAAAAAAAAAAAAAFAEAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFAEAAAAAAAAAAAAAFAGAAAAAAAAAAAAAIA#####wACYjYALihyMz0wKSoxKyhyMz0xKSo1KyhyMz0yKSo3KyhyMz0zKSoxMSsocjM9NCkqMTMAAAAEAAAAAAQAAAAABAAAAAAEAAAAAAQCAAAABAgAAAAFAAAABwAAAAEAAAAAAAAAAAAAAAE#8AAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAE#8AAAAAAAAAAAAAFAFAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFAAAAAAAAAAAAAAAFAHAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFACAAAAAAAAAAAAAFAJgAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFAEAAAAAAAAAAAAAFAKgAAAAAAAAAAAAIA#####wACYjcALChyMz0wKSoxKyhyMz0xKSoyKyhyMz0yKSozKyhyMz0zKSo0KyhyMz00KSo1AAAABAAAAAAEAAAAAAQAAAAABAAAAAAEAgAAAAQIAAAABQAAAAcAAAABAAAAAAAAAAAAAAABP#AAAAAAAAAAAAAEAgAAAAQIAAAABQAAAAcAAAABP#AAAAAAAAAAAAABQAAAAAAAAAAAAAAEAgAAAAQIAAAABQAAAAcAAAABQAAAAAAAAAAAAAABQAgAAAAAAAAAAAAEAgAAAAQIAAAABQAAAAcAAAABQAgAAAAAAAAAAAABQBAAAAAAAAAAAAAEAgAAAAQIAAAABQAAAAcAAAABQBAAAAAAAAAAAAABQBQAAAAAAAAAAAACAP####8AAmI4ACwocjM9MCkqMSsocjM9MSkqMysocjM9MikqNSsocjM9MykqNysocjM9NCkqOQAAAAQAAAAABAAAAAAEAAAAAAQAAAAABAIAAAAECAAAAAUAAAAHAAAAAQAAAAAAAAAAAAAAAT#wAAAAAAAAAAAABAIAAAAECAAAAAUAAAAHAAAAAT#wAAAAAAAAAAAAAUAIAAAAAAAAAAAABAIAAAAECAAAAAUAAAAHAAAAAUAAAAAAAAAAAAAAAUAUAAAAAAAAAAAABAIAAAAECAAAAAUAAAAHAAAAAUAIAAAAAAAAAAAAAUAcAAAAAAAAAAAABAIAAAAECAAAAAUAAAAHAAAAAUAQAAAAAAAAAAAAAUAiAAAAAAAAAAAAAgD#####AAJiOQAsKHIzPTApKjErKHIzPTEpKjIrKHIzPTIpKjQrKHIzPTMpKjUrKHIzPTQpKjcAAAAEAAAAAAQAAAAABAAAAAAEAAAAAAQCAAAABAgAAAAFAAAABwAAAAEAAAAAAAAAAAAAAAE#8AAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAE#8AAAAAAAAAAAAAFAAAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFAAAAAAAAAAAAAAAFAEAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFACAAAAAAAAAAAAAFAFAAAAAAAAAAAAAQCAAAABAgAAAAFAAAABwAAAAFAEAAAAAAAAAAAAAFAHAAAAAAAAAAAAAIA#####wABYgBac2koYT0xLGIxLHNpKGE9MixiMixzaShhPTMsYjMsc2koYT00LGI0LHNpKGE9NSxiNSxzaShhPTYsYjYsc2koYT03LGI3LHNpKGE9OCxiOCxiOSkpKSkpKSkp#####wAAAAEADUNGb25jdGlvbjNWYXIAAAAABAgAAAAFAAAACQAAAAE#8AAAAAAAAAAAAAUAAAAKAAAABgAAAAAECAAAAAUAAAAJAAAAAUAAAAAAAAAAAAAABQAAAAsAAAAGAAAAAAQIAAAABQAAAAkAAAABQAgAAAAAAAAAAAAFAAAADAAAAAYAAAAABAgAAAAFAAAACQAAAAFAEAAAAAAAAAAAAAUAAAANAAAABgAAAAAECAAAAAUAAAAJAAAAAUAUAAAAAAAAAAAABQAAAA4AAAAGAAAAAAQIAAAABQAAAAkAAAABQBgAAAAAAAAAAAAFAAAADwAAAAYAAAAABAgAAAAFAAAACQAAAAFAHAAAAAAAAAAAAAUAAAAQAAAABgAAAAAECAAAAAUAAAAJAAAAAUAgAAAAAAAAAAAABQAAABEAAAAFAAAAEgAAAAIA#####wABZwATcGdjZChhYnMoYSksYWJzKGIpKf####8AAAABAA1DRm9uY3Rpb24yVmFyAgAAAAMAAAAABQAAAAkAAAADAAAAAAUAAAATAAAAAgD#####AAJhJwArc2koYT0wLDEsc2koYWJzKGEpKmFicyhiKTw9NDAwLGFicyhhKS9nLDEpKQAAAAYAAAAABAgAAAAFAAAACQAAAAEAAAAAAAAAAAAAAAE#8AAAAAAAAAAAAAYAAAAABAYAAAAEAgAAAAMAAAAABQAAAAkAAAADAAAAAAUAAAATAAAAAUB5AAAAAAAAAAAABAMAAAADAAAAAAUAAAAJAAAABQAAABQAAAABP#AAAAAAAAAAAAACAP####8AAmInADtzaShiPTAsMSxzaShhYnMoYSkqYWJzKGIpPD00MDAsYWJzKGIpL2csMStpbnQocmFuZCgwKSoxMCkpKQAAAAYAAAAABAgAAAAFAAAAEwAAAAEAAAAAAAAAAAAAAAE#8AAAAAAAAAAAAAYAAAAABAYAAAAEAgAAAAMAAAAABQAAAAkAAAADAAAAAAUAAAATAAAAAUB5AAAAAAAAAAAABAMAAAADAAAAAAUAAAATAAAABQAAABQAAAAEAAAAAAE#8AAAAAAAAAAAAAMCAAAABAIAAAADEQAAAAEAAAAAAAAAAAAAAAAAAAAAAAAAAUAkAAAAAAAAAAAAAgD#####AAJmMQADZj0xAAAABAgAAAAFAAAACAAAAAE#8AAAAAAAAAAAAAIA#####wACZjIAA2Y9MgAAAAQIAAAABQAAAAgAAAABQAAAAAAAAAAAAAACAP####8AAmYzAANmPTMAAAAECAAAAAUAAAAIAAAAAUAIAAAAAAAAAAAAAgD#####AAJmNAADZj00AAAABAgAAAAFAAAACAAAAAFAEAAAAAAAAP####8AAAABAAVDRm9uYwD#####AARmb3IxAAthJyp4XjIrYic9MAAAAAQIAAAABAAAAAAEAgAAAAUAAAAV#####wAAAAEACkNQdWlzc2FuY2X#####AAAAAgARQ1ZhcmlhYmxlRm9ybWVsbGUAAAAAAAAAAUAAAAAAAAAAAAAABQAAABYAAAABAAAAAAAAAAAAAXgAAAAIAP####8ABGZvcjIAC2EnKnheMi1iJz0wAAAABAgAAAAEAQAAAAQCAAAABQAAABUAAAAJAAAACgAAAAAAAAABQAAAAAAAAAAAAAAFAAAAFgAAAAEAAAAAAAAAAAABeAAAAAgA#####wAEZm9yMwANYScqeF4zK2InKng9MAAAAAQIAAAABAAAAAAEAgAAAAUAAAAVAAAACQAAAAoAAAAAAAAAAUAIAAAAAAAAAAAABAIAAAAFAAAAFgAAAAoAAAAAAAAAAQAAAAAAAAAAAAF4AAAACAD#####AARmb3I0AA1hJyp4XjMtYicqeD0wAAAABAgAAAAEAQAAAAQCAAAABQAAABUAAAAJAAAACgAAAAAAAAABQAgAAAAAAAAAAAAEAgAAAAUAAAAWAAAACgAAAAAAAAABAAAAAAAAAAAAAXj#####AAAAAgAGQ0xhdGV4AP####8AAAAAAQAA#####xBARoAAAAAAAEBIKPXCj1woAAAAAAAAAAAAAAAAAAEAAAAAAAAAAABqXElme2YxfQp7ClxGb3JTaW1we2ZvcjF9fQp7ClxJZntmMn0KewpcRm9yU2ltcHtmb3IyfQp9CnsKXElme2YzfQp7ClxGb3JTaW1we2ZvcjN9Cn0KewpcRm9yU2ltcHtmb3I0fQp9Cn0KfQAAAAgA#####wAEemVybwASYWJzKHgpPDAuMDAwMDAwMDAxAAAABAQAAAADAAAAAAoAAAAAAAAAAT4RLgvoJtaVAAF4AAAACAD#####AAZlbnRpZXIADnplcm8oeC1pbnQoeCkp#####wAAAAEADkNBcHBlbEZvbmN0aW9uAAAAIAAAAAQBAAAACgAAAAAAAAADAgAAAAoAAAAAAAF4#####wAAAAEACUNGb25jTlZhcgD#####AANkaXYADWVudGllcih4L3leMikAAAAMAAAAIQAAAAQDAAAACgAAAAAAAAAJAAAACgAAAAEAAAABQAAAAAAAAAAAAAACAAF4AAF5AAAACAD#####AAxleHRyYWl0Y2FycmUBNHNpKGRpdih4LDIwKSwyMCxzaShkaXYoeCwxOSksMTksc2koZGl2KHgsMTgpLDE4LHNpKGRpdih4LDE3KSwxNyxzaShkaXYoeCwxNiksMTYsc2koZGl2KHgsMTUpLDE1LHNpKGRpdih4LDE0KSwxNCxzaShkaXYoeCwxMyksMTMsc2koZGl2KHgsMTIpLDEyLHNpKGRpdih4LDExKSwxMSxzaShkaXYoeCwxMCksMTAsc2koZGl2KHgsOSksOSxzaShkaXYoeCw4KSw4LHNpKGRpdih4LDcpLDcsc2koZGl2KHgsNiksNixzaShkaXYoeCw1KSw1LHNpKGRpdih4LDQpLDQsc2koZGl2KHgsMyksMyxzaShkaXYoeCwyKSwyLDEpKSkpKSkpKSkpKSkpKSkpKSkpAAAABgD#####AAAAAQASQ0FwcGVsRm9uY3Rpb25OVmFyAAAAAgAAACIAAAAKAAAAAAAAAAFANAAAAAAAAAAAAAFANAAAAAAAAAAAAAYAAAAADgAAAAIAAAAiAAAACgAAAAAAAAABQDMAAAAAAAAAAAABQDMAAAAAAAAAAAAGAAAAAA4AAAACAAAAIgAAAAoAAAAAAAAAAUAyAAAAAAAAAAAAAUAyAAAAAAAAAAAABgAAAAAOAAAAAgAAACIAAAAKAAAAAAAAAAFAMQAAAAAAAAAAAAFAMQAAAAAAAAAAAAYAAAAADgAAAAIAAAAiAAAACgAAAAAAAAABQDAAAAAAAAAAAAABQDAAAAAAAAAAAAAGAAAAAA4AAAACAAAAIgAAAAoAAAAAAAAAAUAuAAAAAAAAAAAAAUAuAAAAAAAAAAAABgAAAAAOAAAAAgAAACIAAAAKAAAAAAAAAAFALAAAAAAAAAAAAAFALAAAAAAAAAAAAAYAAAAADgAAAAIAAAAiAAAACgAAAAAAAAABQCoAAAAAAAAAAAABQCoAAAAAAAAAAAAGAAAAAA4AAAACAAAAIgAAAAoAAAAAAAAAAUAoAAAAAAAAAAAAAUAoAAAAAAAAAAAABgAAAAAOAAAAAgAAACIAAAAKAAAAAAAAAAFAJgAAAAAAAAAAAAFAJgAAAAAAAAAAAAYAAAAADgAAAAIAAAAiAAAACgAAAAAAAAABQCQAAAAAAAAAAAABQCQAAAAAAAAAAAAGAAAAAA4AAAACAAAAIgAAAAoAAAAAAAAAAUAiAAAAAAAAAAAAAUAiAAAAAAAAAAAABgAAAAAOAAAAAgAAACIAAAAKAAAAAAAAAAFAIAAAAAAAAAAAAAFAIAAAAAAAAAAAAAYAAAAADgAAAAIAAAAiAAAACgAAAAAAAAABQBwAAAAAAAAAAAABQBwAAAAAAAAAAAAGAAAAAA4AAAACAAAAIgAAAAoAAAAAAAAAAUAYAAAAAAAAAAAAAUAYAAAAAAAAAAAABgAAAAAOAAAAAgAAACIAAAAKAAAAAAAAAAFAFAAAAAAAAAAAAAFAFAAAAAAAAAAAAAYAAAAADgAAAAIAAAAiAAAACgAAAAAAAAABQBAAAAAAAAAAAAABQBAAAAAAAAAAAAAGAAAAAA4AAAACAAAAIgAAAAoAAAAAAAAAAUAIAAAAAAAAAAAAAUAIAAAAAAAAAAAABgAAAAAOAAAAAgAAACIAAAAKAAAAAAAAAAFAAAAAAAAAAAAAAAFAAAAAAAAAAAAAAAE#8AAAAAAAAAABeAAAAAIA#####wAFbmJTb2wAHHNpKGYxLDAsc2koZjIsMixzaShmMywxLDMpKSkAAAAGAAAAAAUAAAAXAAAAAQAAAAAAAAAAAAAABgAAAAAFAAAAGAAAAAFAAAAAAAAAAAAAAAYAAAAABQAAABkAAAABP#AAAAAAAAAAAAABQAgAAAAAAAAAAAACAP####8AAWsAE2V4dHJhaXRjYXJyZShiJyphJykAAAAMAAAAIwAAAAQCAAAABQAAABYAAAAFAAAAFQAAAAIA#####wABcQAJYicqYScva14yAAAABAMAAAAEAgAAAAUAAAAWAAAABQAAABUAAAAJAAAABQAAACUAAAABQAAAAAAAAAAAAAACAP####8ACnRvbWJlanVzdGUACXplcm8ocS0xKQAAAAwAAAAgAAAABAEAAAAFAAAAJgAAAAE#8AAAAAAAAAAAAAIA#####wACZycACnBnY2QoayxhJykAAAAHAgAAAAUAAAAlAAAABQAAABUAAAACAP####8AAmsnAARrL2cnAAAABAMAAAAFAAAAJQAAAAUAAAAoAAAAAgD#####AAJkJwAFYScvZycAAAAEAwAAAAUAAAAVAAAABQAAACgAAAACAP####8AAngxAA1rJypzcXJ0KHEpL2QnAAAABAMAAAAEAgAAAAUAAAApAAAAAwEAAAAFAAAAJgAAAAUAAAAqAAAAAgD#####AAJ4MgADLXgx#####wAAAAEADENNb2luc1VuYWlyZQAAAAUAAAArAAAAAgD#####AAJ4MwABMAAAAAEAAAAAAAAAAAAAAAgA#####wADcmVwAAEwAAAAAQAAAAAAAAAAAAF4AAAACAD#####AARsZWZ0AA5nYXVjaGUocmVwKHgpKQAAAAMUAAAADAAAAC4AAAAKAAAAAAABeAAAAAgA#####wAFcmlnaHQADWRyb2l0KHJlcCh4KSkAAAADFQAAAAwAAAAuAAAACgAAAAAAAXgAAAAIAP####8AA2RpZgAQbGVmdCh4KS1yaWdodCh4KQAAAAQBAAAADAAAAC8AAAAKAAAAAAAAAAwAAAAwAAAACgAAAAAAAXgAAAACAP####8ACGVzdFNvbHgxAA16ZXJvKGRpZih4MSkpAAAADAAAACAAAAAMAAAAMQAAAAUAAAArAAAAAgD#####AAhlc3RTb2x4MgANemVybyhkaWYoeDIpKQAAAAwAAAAgAAAADAAAADEAAAAFAAAALAAAAAIA#####wAIZXN0U29seDMADXplcm8oZGlmKHgzKSkAAAAMAAAAIAAAAAwAAAAxAAAABQAAAC0AAAACAP####8AB3JhY2luZTEAJHNpKGYyfGY0LGVzdFNvbHgxLHNpKGYzLGVzdFNvbHgzLDApKQAAAAYAAAAABAsAAAAFAAAAGAAAAAUAAAAaAAAABQAAADIAAAAGAAAAAAUAAAAZAAAABQAAADQAAAABAAAAAAAAAAAAAAACAP####8AB3JhY2luZTIAFHNpKGYyfGY0LGVzdFNvbHgyLDApAAAABgAAAAAECwAAAAUAAAAYAAAABQAAABoAAAAFAAAAMwAAAAEAAAAAAAAAAAAAAAIA#####wAHcmFjaW5lMwARc2koZjQsZXN0U29seDMsMCkAAAAGAAAAAAUAAAAaAAAABQAAADQAAAABAAAAAAAAAAAAAAAIAP####8ABHNvbDEAD3g9aycqc3FydChxKS9kJwAAAAQIAAAACgAAAAAAAAAEAwAAAAQCAAAABQAAACkAAAADAQAAAAUAAAAmAAAABQAAACoAAXgAAAAIAP####8ABXNvbCcxAAd4PWsnL2QnAAAABAgAAAAKAAAAAAAAAAQDAAAABQAAACkAAAAFAAAAKgABeAAAAAgA#####wAEc29sMgAQeD0taycqc3FydChxKS9kJwAAAAQIAAAACgAAAAAAAAAPAAAABAMAAAAEAgAAAAUAAAApAAAAAwEAAAAFAAAAJgAAAAUAAAAqAAF4AAAACAD#####AAVzb2wnMgAIeD0taycvZCcAAAAECAAAAAoAAAAAAAAADwAAAAQDAAAABQAAACkAAAAFAAAAKgABeAAAAAgA#####wAEc29sMwADeD0wAAAABAgAAAAKAAAAAAAAAAEAAAAAAAAAAAABeP####8AAAADABBDVGVzdEVxdWl2YWxlbmNlAP####8ABHRlcTEAAAA4AAAALgEAAAAAAT#wAAAAAAAAAQAAABAA#####wAFdGVxJzEAAAA5AAAALgEAAAAAAT#wAAAAAAAAAQAAABAA#####wAEdGVxMgAAADoAAAAuAQAAAAABP#AAAAAAAAABAAAAEAD#####AAV0ZXEnMgAAADsAAAAuAQAAAAABP#AAAAAAAAABAAAAEAD#####AAR0ZXEzAAAAPAAAAC4BAAAAAAE#8AAAAAAAAAEAAAACAP####8ABnJlc29sdQB7c2koZjIsc2kodG9tYmVqdXN0ZSx0ZXEnMSsyKnRlcScyLHRlcTErMip0ZXEyKSxzaShmMyx0ZXEzLHNpKGY0LHNpKHRvbWJlanVzdGUsdGVxJzErMip0ZXEnMiszKnRlcTMsdGVxMSsyKnRlcTIrMyp0ZXEzKSwwKSkpAAAABgAAAAAFAAAAGAAAAAYAAAAABQAAACcAAAAEAAAAAAUAAAA+AAAABAIAAAABQAAAAAAAAAAAAAAFAAAAQAAAAAQAAAAABQAAAD0AAAAEAgAAAAFAAAAAAAAAAAAAAAUAAAA#AAAABgAAAAAFAAAAGQAAAAUAAABBAAAABgAAAAAFAAAAGgAAAAYAAAAABQAAACcAAAAEAAAAAAQAAAAABQAAAD4AAAAEAgAAAAFAAAAAAAAAAAAAAAUAAABAAAAABAIAAAABQAgAAAAAAAAAAAAFAAAAQQAAAAQAAAAABAAAAAAFAAAAPQAAAAQCAAAAAUAAAAAAAAAAAAAABQAAAD8AAAAEAgAAAAFACAAAAAAAAAAAAAUAAABBAAAAAQAAAAAAAAAAAAAACAD#####AAJJZAABeAAAAAoAAAAAAAF4AAAAEAD#####AApnYXVjaGVFc3R4AAAALwAAAEMBAAAAAAE#8AAAAAAAAAEAAAAQAP####8ACWRyb2l0RXN0eAAAADAAAABDAQAAAAABP#AAAAAAAAAB#####wAAAAEAF0NUZXN0RGVwZW5kYW5jZVZhcmlhYmxlAP####8ACmdhdWNoZURlcHgAAAAvAAAAAAAAABEA#####wAJZHJvaXREZXB4AAAAMAAAAAAAAAACAP####8ACXh1bkVzdFNvbAA4KGdhdWNoZUVzdHgmMS1kcm9pdERlcHh8ZHJvaXRFc3R4JjEtZ2F1Y2hlRGVweCkmZXN0U29seDEAAAAECgAAAAQLAAAABAoAAAAFAAAARAAAAAQBAAAAAT#wAAAAAAAAAAAABQAAAEcAAAAECgAAAAUAAABFAAAABAEAAAABP#AAAAAAAAAAAAAFAAAARgAAAAUAAAAyAAAAAgD#####AAt4ZGV1eEVzdFNvbAA4KGdhdWNoZUVzdHgmMS1kcm9pdERlcHh8ZHJvaXRFc3R4JjEtZ2F1Y2hlRGVweCkmZXN0U29seDIAAAAECgAAAAQLAAAABAoAAAAFAAAARAAAAAQBAAAAAT#wAAAAAAAAAAAABQAAAEcAAAAECgAAAAUAAABFAAAABAEAAAABP#AAAAAAAAAAAAAFAAAARgAAAAUAAAAzAAAAAgD#####AAx4dHJvaXNFc3RTb2wAOChnYXVjaGVFc3R4JjEtZHJvaXREZXB4fGRyb2l0RXN0eCYxLWdhdWNoZURlcHgpJmVzdFNvbHgzAAAABAoAAAAECwAAAAQKAAAABQAAAEQAAAAEAQAAAAE#8AAAAAAAAAAAAAUAAABHAAAABAoAAAAFAAAARQAAAAQBAAAAAT#wAAAAAAAAAAAABQAAAEYAAAAFAAAANAAAAAIA#####wAFZXhhY3QAU3NpKGYyLHh1bkVzdFNvbCsyKnhkZXV4RXN0U29sLHNpKGYzLHh0cm9pc0VzdFNvbCxzaShmNCx4dW5Fc3RTb2wrMip4ZGV1eEVzdFNvbCwwKSkpAAAABgAAAAAFAAAAGAAAAAQAAAAABQAAAEgAAAAEAgAAAAFAAAAAAAAAAAAAAAUAAABJAAAABgAAAAAFAAAAGQAAAAUAAABKAAAABgAAAAAFAAAAGgAAAAQAAAAABQAAAEgAAAAEAgAAAAFAAAAAAAAAAAAAAAUAAABJAAAAAQAAAAAAAAAAAAAAAgD#####AAJrIgAQZXh0cmFpdGNhcnJlKGEnKQAAAAwAAAAjAAAABQAAABUAAAACAP####8AAnEiAAdhJy9rIl4yAAAABAMAAAAFAAAAFQAAAAkAAAAFAAAATAAAAAFAAAAAAAAAAAAAAAIA#####wAMZGVub21zaW1wbGlmAAwxLXplcm8oayItMSkAAAAEAQAAAAE#8AAAAAAAAAAAAAwAAAAgAAAABAEAAAAFAAAATAAAAAE#8AAAAAAAAAAAAAIA#####wANZGVub21lc3RjYXJyZQAKemVybyhxIi0xKQAAAAwAAAAgAAAABAEAAAAFAAAATQAAAAE#8AAAAAAAAAAAAAIA#####wACbmQABWInKmEnAAAABAIAAAAFAAAAFgAAAAUAAAAVAAAAAgD#####AAJkZAAEYSdeMgAAAAkAAAAFAAAAFQAAAAFAAAAAAAAAAAAAAAgA#####wAFZm9ybTEACGEqeF4yPj0wAAAABAcAAAAEAgAAAAUAAAAJAAAACQAAAAoAAAAAAAAAAUAAAAAAAAAAAAAAAQAAAAAAAAAAAAF4AAAACAD#####AAVmb3JtMgAKYSp4XjIrYj49YgAAAAQHAAAABAAAAAAEAgAAAAUAAAAJAAAACQAAAAoAAAAAAAAAAUAAAAAAAAAAAAAABQAAABMAAAAFAAAAEwABeAAAAAgA#####wAFZm9ybTMACXheMj1iJy9hJwAAAAQIAAAACQAAAAoAAAAAAAAAAUAAAAAAAAAAAAAABAMAAAAFAAAAFgAAAAUAAAAVAAF4AAAACAD#####AAVmb3JtNAANeD1zcXJ0KGInL2EnKQAAAAQIAAAACgAAAAAAAAADAQAAAAQDAAAABQAAABYAAAAFAAAAFQABeAAAAAgA#####wAGZm9ybSc0AA54PS1zcXJ0KGInL2EnKQAAAAQIAAAACgAAAAAAAAAPAAAAAwEAAAAEAwAAAAUAAAAWAAAABQAAABUAAXgAAAAIAP####8ABWZvcm01AA14PXNxcnQobmQvZGQpAAAABAgAAAAKAAAAAAAAAAMBAAAABAMAAAAFAAAAUAAAAAUAAABRAAF4AAAACAD#####AAZmb3JtJzUADng9LXNxcnQobmQvZGQpAAAABAgAAAAKAAAAAAAAAA8AAAADAQAAAAQDAAAABQAAAFAAAAAFAAAAUQABeAAAAAgA#####wAFZm9ybTYAGHg9c3FydChiJykvKGsiKnNxcnQocSIpKQAAAAQIAAAACgAAAAAAAAAEAwAAAAMBAAAABQAAABYAAAAEAgAAAAUAAABMAAAAAwEAAAAFAAAATQABeAAAAAgA#####wAGZm9ybSc2ABl4PS1zcXJ0KGInKS8oayIqc3FydChxIikpAAAABAgAAAAKAAAAAAAAAA8AAAAEAwAAAAMBAAAABQAAABYAAAAEAgAAAAUAAABMAAAAAwEAAAAFAAAATQABeAAAAAgA#####wAIZm9yZmFjdDMAD3gqKGEnKnheMitiJyk9MAAAAAQIAAAABAIAAAAKAAAAAAAAAAQAAAAABAIAAAAFAAAAFQAAAAkAAAAKAAAAAAAAAAFAAAAAAAAAAAAAAAUAAAAWAAAAAQAAAAAAAAAAAAF4AAAACAD#####AAhmb3JmYWN0NAAPeCooYScqeF4yLWInKT0wAAAABAgAAAAEAgAAAAoAAAAAAAAABAEAAAAEAgAAAAUAAAAVAAAACQAAAAoAAAAAAAAAAUAAAAAAAAAAAAAABQAAABYAAAABAAAAAAAAAAAAAXgAAAALAP####8AAAAAAQAIc29sdXRpb27#####EEBEgAAAAAAAQFZUeuFHrhQAAAAAAAAAAAAAAAAAAQAAAAAAAAAACFVcYmVnaW57YXJyYXl9e2x9ClxJZntmMX0KewpcdGV4dHtQb3VyIHRvdXQgcsOpZWwgJHgkLCAkeMKyXGdlMCQgZG9uYyAkXEZvclNpbXB7Zm9ybTF9JCBkb25jICRcRm9yU2ltcHtmb3JtMn0kfQpcXCBcdGV4dHtMJ8OpcXVhdGlvbiAkXEZvclNpbXB7Zm9yMX0kIG4nYSBkb25jIHBhcyBkZSBzb2x1dGlvbi59Cn0KewpcSWZ7ZjJ9CnsKXHRleHR7JFxGb3JTaW1we2ZvcjJ9XExlZnRyaWdodGFycm93IFxGb3JTaW1we2Zvcm0zfSBcTGVmdHJpZ2h0YXJyb3cgXEZvclNpbXB7Zm9ybSc0fSQgb3UgJFxGb3JTaW1we2Zvcm00fSR9ClxJZnt0b21iZWp1c3RlfQp7ClxcXHRleHR7JFxGb3JTaW1we2ZvcjJ9XExlZnRyaWdodGFycm93IFxGb3JTaW1we3NvbCcyfSQgb3UgJFxGb3JTaW1we3NvbCcxfSR9Cn0KewpcSWZ7ZGVub21lc3RjYXJyZX0KewpcXCBcdGV4dHskXEZvclNpbXB7Zm9yMn1cTGVmdHJpZ2h0YXJyb3cgXEZvclNpbXB7c29sMn0kIG91ICRcRm9yU2ltcHtzb2wxfSR9Cn0KewpcSWZ7ZGVub21zaW1wbGlmfQp7ClxcIFx0ZXh0eyRcRm9yU2ltcHtmb3IyfVxMZWZ0cmlnaHRhcnJvdyBcRm9yU2ltcHtmb3JtJzZ9JCBvdSAkXEZvclNpbXB7Zm9ybTZ9JH0KXFwgXHRleHR7RW4gbXVsdGlwbGlhbnQgbnVtw6lyYXRldXIgZXQgZMOpbm9taW5hdGV1ciBwYXIgJFxzcXJ0e1xWYWx7cSJ9fSQgOn0KXFwgXHRleHR7JFxGb3JTaW1we2ZvcjJ9XExlZnRyaWdodGFycm93IFxGb3JTaW1we3NvbDJ9JCBvdSRcRm9yU2ltcHtzb2wxfSR9Cn0KewpcXCBcdGV4dHskXEZvclNpbXB7Zm9yMn1cTGVmdHJpZ2h0YXJyb3cgXEZvclNpbXB7Zm9ybSc1fSQgb3UgJFxGb3JTaW1we2Zvcm01fSR9ClxcIFx0ZXh0eyRcRm9yU2ltcHtmb3IyfVxMZWZ0cmlnaHRhcnJvdyBcRm9yU2ltcHtzb2wyfSQgb3UgJFxGb3JTaW1we3NvbDF9JH0KfQp9Cn0KfQp7ClxJZntmM30KewpcXCBcdGV4dHskXEZvclNpbXB7Zm9yM30gXExlZnRyaWdodGFycm93IFxGb3JTaW1we2ZvcmZhY3QzfSR9ClxcIFx0ZXh0eyRcRm9yU2ltcHtmb3IzfSBcTGVmdHJpZ2h0YXJyb3cgeD0wJCBvdSAkXEZvclNpbXB7Zm9yMX0kfQpcXCBcdGV4dHtQb3VyIHRvdXQgcsOpZWwgJHgkLCAkeMKyXGdlMCQgZG9uYyAkXEZvclNpbXB7Zm9ybTF9JCBkb25jICRcRm9yU2ltcHtmb3JtMn0kfQpcXCBcdGV4dHtEb25jIGxhIHNldWxlIHNvbHV0aW9uIGRlIGwnw6lxdWF0aW9uIGVzdCAkeD0wJH0uCn0KewpcXCBcdGV4dHskXEZvclNpbXB7Zm9yNH0gXExlZnRyaWdodGFycm93IFxGb3JTaW1we2ZvcmZhY3Q0fSR9ClxcIFx0ZXh0eyRcRm9yU2ltcHtmb3I0fVxMZWZ0cmlnaHRhcnJvdyB4PSAwJCBvdSAkXEZvclNpbXB7Zm9ybTN9IFxMZWZ0cmlnaHRhcnJvdyB4PTAgJCBvdSAkXEZvclNpbXB7Zm9ybSc0fSQgb3UgJFxGb3JTaW1we2Zvcm00fSR9ClxJZnt0b21iZWp1c3RlfQp7ClxcXHRleHR7JFxGb3JTaW1we2ZvcjR9XExlZnRyaWdodGFycm93IHg9MCAkIG91ICRcRm9yU2ltcHtzb2wnMn0kIG91ICRcRm9yU2ltcHtzb2wnMX0kfQp9CnsKXElme2Rlbm9tZXN0Y2FycmV9CnsKXFwgXHRleHR7JFxGb3JTaW1we2ZvcjR9XExlZnRyaWdodGFycm93IHg9MCQgb3UgJFxGb3JTaW1we3NvbDJ9JCBvdSRcRm9yU2ltcHtzb2wxfSR9Cn0KewpcSWZ7ZGVub21zaW1wbGlmfQp7ClxcIFx0ZXh0eyRcRm9yU2ltcHtmb3I0fVxMZWZ0cmlnaHRhcnJvdyB4PTAkIG91ICRcRm9yU2ltcHtmb3JtJzZ9JCBvdSAkXEZvclNpbXB7Zm9ybTZ9JH0KXFwgXHRleHR7RW4gbXVsdGlwbGlhbnQgbnVtw6lyYXRldXIgZXQgZMOpbm9taW5hdGV1ciBkZXMgc29sdXRpb25zIG5vbiBudWxsZXMgcGFyICRcc3FydHtcVmFse3EifX0kIDp9ClxcIFx0ZXh0eyRcRm9yU2ltcHtmb3I0fVxMZWZ0cmlnaHRhcnJvdyB4PTAkIG91ICRcRm9yU2ltcHtzb2wyfSQgb3UkXEZvclNpbXB7c29sMX0kfQp9CnsKXFwgXHRleHR7JFxGb3JTaW1we2ZvcjR9XExlZnRyaWdodGFycm93IHg9MCQgb3UgJCBcRm9yU2ltcHtmb3JtJzV9JCBvdSAkXEZvclNpbXB7Zm9ybTV9JH0KXFwgXHRleHR7JFxGb3JTaW1we2ZvcjJ9XExlZnRyaWdodGFycm93IHg9MCQgb3UgJFxGb3JTaW1we3NvbDJ9JCBvdSAkXEZvclNpbXB7c29sMX0kfQp9Cn0KfQp9Cn0KfQpcXCAKXGVuZHthcnJheX3###############8=
Sinon :
Utilisez l'icône  de création d'une nouvelle figure et choisissez de créer une Figure sans repère et sans longueur unité.
de création d'une nouvelle figure et choisissez de créer une Figure sans repère et sans longueur unité.
Notre figure servira à fournir l'équation à résoudre, des objets numériques servant à savoir à quel stade de résolution en est l'élève et à afficher après la réponse finale une figure d'explication.
Les équations proposées seront (dans un ordre aléatoire) :
- ax² + b = 0
- ax² - b = 0
- ax^3 + bx = 0
- ax^3 - bx = 0
Nous ferons en sorte que a et b soient strictement positifs et premiers entre eux.
A l'aide de l'icône ![]() créez les calculs réels suivants :
créez les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| nbvar | 3 | Déclare le nombre de calculs aléatoires utilisés par la figure |
| nbcas1 | 4 | Le calcul nommé r1 pourra prendre 4 valeurs entières de 0 à 3 |
| nbcas2 | 9 | Le calcul nommé r2 pourra prendre 9 valeurs entières de 0 à 8 |
| nbcas3 | 5 | Le calcul nommé r3 pourra prendre 5 valeurs entières de 0 à 4 |
| r1 | int(rand(0)*nbcas1) | r1 pourra prendre les valeurs entières de 0 à 3 |
| r2 | int(rand(0)*nbcas2) | r2 pourra prendre les valeurs entières de 0 à 8 |
| r3 | int(rand(0)*nbcas3) | r3 pourra prendre les valeurs entières de 0 à 4 |
La création de ces calculs est indispensable pour que la ressource j3p associée donne lors des répétitions successives des valeurs à r1, r2, r3 toutes distinctes les unes des autres.
Par exemple il sera donné à r1 des valeurs distinctes successives comprises entre 0 et 3 lors des répétitions (car nbcas1 est égal à 4) et à r3 des valeurs distinctes successives comprises entre 0 et 4 (car nbcas3 est égal à 5).
Les formules que nous mettons dans r1, r2, r3 ne servent donc qu'à simuler les formules qui seront mises dans ces calculs lors des répétitions successives.
Créez maintenant les calculs réels suivants (icône ![]() ) :
) :
| Nom du calcul | Formule | Explication |
|---|---|---|
| f | 1+r1 | Prend les valeurs 1 à 4 pour savoir quelle est l'équation proposée |
| a | 1+r2 | Prend des valeurs de 1 à 9 |
| b1 | r3+2 | Valeurs que pourra prendre b si a = 1 |
| b2 | (r3=0)*1+(r3=1)*3+(r3=2)*5 +(r3=3)*7+(r3=4)*9 | Valeurs que pourra prendre b si a = 2, soit 1, 3, 5, 7 ou 9 |
| b3 | (r3=0)*1+(r3=1)*2+(r3=2)*4 +(r3=3)*5+(r3=4)*7 | Valeurs que pourra prendre b si a = 3, soit 1, 2, 4, 5 ou 7 |
| b4 | (r3=0)*1+(r3=1)*3+(r3=2)*5 +(r3=3)*7+(r3=4)*9 | Valeurs que pourra prendre b si a = 4, soit 1, 3, 5, 7 ou 9 |
| b5 | (r3=0)*1+(r3=1)*2+(r3=2)*3 +(r3=3)*4+(r3=4)*6 | Valeurs que pourra prendre b si a = 5, soit 1, 2, 3, 4 ou 6 |
| b6 | (r3=0)*1+(r3=1)*5+(r3=2)*7 +(r3=3)*11+(r3=4)*13 | Valeurs que pourra prendre b si a = 6, soit 1, 5, 7, 11 ou 13 |
| b7 | (r3=0)*1+(r3=1)*2+(r3=2)*3 +(r3=3)*4+(r3=4)*5 | Valeurs que pourra prendre b si a = 7, soit 1, 2, 3, 4 ou 5 |
| b8 | (r3=0)*1+(r3=1)*3+(r3=2)*5 +(r3=3)*7+(r3=4)*9 | Valeurs que pourra prendre b si a = 8, soit 1, 3, 5, 7 ou 9 |
| b9 | (r3=0)*1+(r3=1)*2+(r3=2)*4 +(r3=3)*5+(r3=4)*7 | Valeurs que pourra prendre b si a = 9, soit 1, 2, 4, 5 ou 7 |
| b | si(a=1,b1,si(a=2,b2,si(a=3,b3,si(a=4, b4,si(a=5,b5,si(a=6,b6,si(a=7,b7,si(a=8,b8,b9)))))))) | Affecte à b une valeur de façon que a et b soient premiers entre eux |
| g | pgcd(abs(a),abs(b)) | |
| a' | si(a=0,1,si(abs(a)*abs(b)<=400, abs(a)/g,1)) | Remplace la valeur de a si a et b sont trop grands ou non premiers entre eux |
| b' | si(b=0,1,si(abs(a)*abs(b)<=400, abs(b)/g,1+int(rand(0)*10))) | Remplace la valeur de b si a et b sont trop grands ou non premiers entre eux |
Un petit complément sur les trois derniers calculs ci-dessus.
On pourrait se demander l'utilité de diviser a et b par leur pgcd puisque nous avons fait en sorte qu'ils soient toujours premiers entre eux. Mais nous allons donner à l'utilisateur la possibilité de donner ses propres valeurs à a et b via la paramétrage de la ressource. a et b ne doivent pas être trop grands pour que la méthode que nous allons utiliser pour extraire le plus grand entier possible de la racine carrée fonctionne.
Créez maintenant les quatre calculs suivants qui nous serviront à faire plus tard des affichages conditionnels.
| Nom de calcul | Formule | Explication |
|---|---|---|
| f1 | f=1 | Renvoie 1 si f est égal à 1 et 0 sinon |
| f2 | f=2 | Renvoie 1 si f est égal à 2 et 0 sinon |
| f3 | f=3 | Renvoie 1 si f est égal à 3 et 0 sinon |
| f4 | f=4 | Renvoie 1 si f est égal à 4 et 0 sinon |
Nous allons maintenant créer quatre fonctions réelles de la variable x qui serviront à afficher l'équation à résoudre.
| Nom de la fonction | Variable formelle | Formule |
|---|---|---|
| for1 | x | a'*x^2+b'=0 |
| for2 | x | a'*x^2-b'=0 |
| for3 | x | a'*x^3+b'*x=0 |
| for4 | x | a'*x^3-b'*x=0 |
Nous allons d'abord créer un premier affichage LaTeX libre qui servira à donner l'équation à résoudre.
Utilisez l'icône ![]() , cliquez en haut de la figure et à gauche de la figure, et entrez comme code LaTeX le code suivant :
, cliquez en haut de la figure et à gauche de la figure, et entrez comme code LaTeX le code suivant :
\If{f1}
{
\ForSimp{for1}}
{
\If{f2}
{
\ForSimp{for2}
}
{
\If{f3}
{
\ForSimp{for3}
}
{
\ForSimp{for4}
}
}
}
Cet affichage LaTeX utilise des affichages conditionnels \If spécifiques à MathGraph32 pour afficher l'équation à résoudre suivant la valeur de f (comprise entre 1 et 4).
Il sera fourni à la ressource pour que cette équation soit affichée dans la consigne et il est impératif que cet affichage soit le premier affichage LaTeX de la figure.
Utilisez maintenant l'outil ![]() pour créer les fonctions de la variable réelle x suivantes :
pour créer les fonctions de la variable réelle x suivantes :
| Nom de la fonction | Variable formelle | Formule | Commentaire |
|---|---|---|---|
| zero | x | abs(x)<0.000000001 | Sert à vérifier les réponses de l'élève à 'epsilon' près |
| rep | x | 0 | Servira à contenir les équations proposées par l'élève |
Avec l'outil ![]() créez les calculs réels suivants :
créez les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| nbSol | si(f1,0,si(f2,2,si(f3,1,3))) | La figure doit impérativement contenir un calcul nommé nbSol qui renvoie le nombre de solutions de l'équation proposée |
| k | divmaxp(b'*a',2) | Renvoie le plus grand entier dont le carré divise le produit b'*a' |
| q | b'*a'/k^2 | Renvoie ce qui restera sous la racine carrée une fois le plus grand entier extrait de celle-ci |
| tombejuste | zero(q-1) | Renvoie 1 si a'*b' est un carré parfait |
| g' | pgcd(k,a') | Renvoie le pgcd de k et de a' |
| k' | k/g' | |
| d' | a'/g' | |
| x1 | k'*sqrt(q)/d' | Renvoie une des 3 racines quand il y en a |
| x2 | -x1 | Renvoie l'opposée de la racine précédente |
| x3 | 0 | La racine nulle |
A noter : quand, par exemple, vous créez le calcul k, quand vous cliquez sur le bouton Fonctions, une liste vous présente toutes les fonctions prédéfinies et que vous trouverez dans la liste divmaxp et sa syntaxe :
divmaxp(n,p): Renvoie le plus grand nombre entier positif k tel que k^p divise n avec 1 < p < 256 et 1 < |n| < 1000000
Les réponses de l'élève (séparées par des ;) sont forcément des équations dont des formules comportant une seule égalité. Ces formules sont mises dans la fonction rep lors de l'évaluation de la réponse les unes après les autres.
Si, par exemple nbSol renvoie 3 comme valeur, notre figure doit contenir des calculs nommés racine1, racine2 et racine3.
racine1 doit renvoyer 1 si ce que nous considérons comme étant la première racine est solution de l'équation figurant dans rep, racine2 doit renvoyer 2 si ce que nous considérons comme étant la deuxième racine est solution de l'équation figurant dans rep et ainsi de suite.
Utilisez l'outil ![]() pour créer les fonctions de la variable réelle x suivantes :
pour créer les fonctions de la variable réelle x suivantes :
| Nom de la fonction | Variable | Formule | Commentaire |
|---|---|---|---|
| left | x | gauche(rep(x)) | Renvoie le membre de gauche de l'égalité contenue dans rep |
| droit | x | droit(rep(x)) | Renvoie le membre de gauche de l'égalité contenue dans rep |
| dif | x | left(x)-right(x) | Renvoie la formule de la fonction qui renvoie la différence des deux membres de l'égalité contenue dans rep |
Créez maintenant les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| estSolx1 | zero(dif(x1)) | revoie 1 si x1 est solution de l'équation contenue dans rep |
| estSolx2 | zero(dif(x2)) | revoie 1 si x2 est solution de l'équation contenue dans rep |
| estSolx3 | zero(dif(x3)) | revoie 1 si x3 est solution de l'équation contenue dans rep |
| racine1 | si(f2|f4,estSolx1,si(f3,estSolx3,0)) | Renvoie 1 si la racine n°1 est racine de l'équation contenue dans rep |
| racine2 | si(f2|f4,estSolx2,0) | Renvoie 1 si la racine n°2 est racine de l'équation contenue dans rep |
| racine3 | si(f4,estSolx3,0) | Renvoie 1 si la racine n°3 est racine de l'équation contenue dans rep |
Utilisez l'outil ![]() pour créer les fonctions de la variable réelle x suivantes :
pour créer les fonctions de la variable réelle x suivantes :
| Nom de la fonction | Variable | Formule | Commentaire |
|---|---|---|---|
| sol1 | x | x=k'*sqrt(q)/d' | Contient la formule simplifiée que doit rentrer l'élève pour une des racines quand la solution ne 'tombe pas juste' |
| sol'1 | x | x=k'/d' | Contient la formule simplifiée que doit rentrer l'élève pour la racine ci-dessus quand la solution 'tombe juste' |
| sol2 | x | x=-k'*sqrt(q)/d' | Contient la formule simplifiée que doit rentrer l'élève pour l'autre racine non nulle quand la solution ne 'tombe pas juste' |
| sol'2 | x | x=-k'/d' | Contient la formule simplifiée que doit rentrer l'élève pour la racine ci-dessus quand la solution 'tombe juste' |
| sol3 | x | x=0 | Formule simplifiée que l'élève doit rentrer pour la solution nulle |
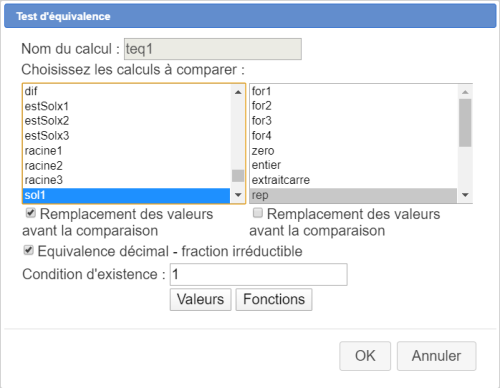
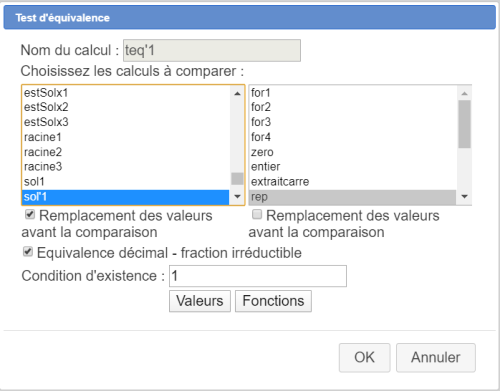
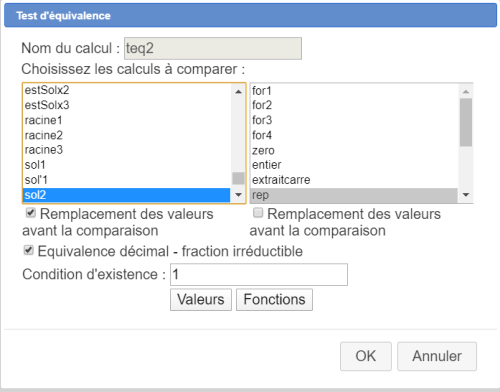
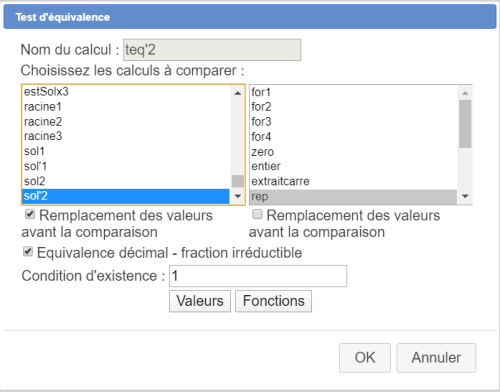
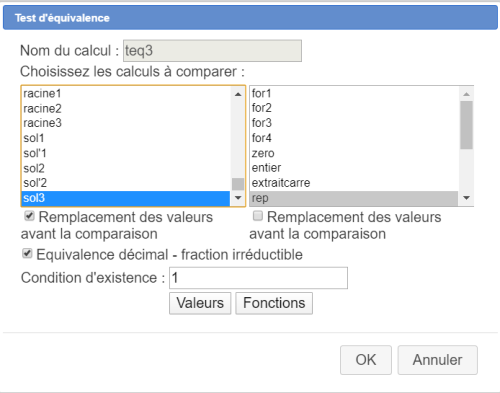
Nous allons maintenant créer cinq tests d'équivalence destinés à savoir si la formule contenue dans la fonction rep peut être considérée comme équivalente aux formules contenues dans les cinq fonctions que nous avons créées ci-dessus.
Ces cinq tests d'équivalence sont créés en cliquant sur l'icône ![]() puis en choisissant Test d'équivalence dans la liste proposée.
puis en choisissant Test d'équivalence dans la liste proposée.
Créez les comme ci-dessous :
Notre figure doit contenir un calcul nommé resolu qui renvoie comme valeur 1 si la réponse est équivalente à ce que nous considérons comme la première réponse exacte, 2 si la réponse est équivalente à ce que nous considérons comme la première réponse exacte et ainsi de suite et 0 si elle ne correspond à aucune bonne réponse (donc ici 0, 1, 2 ou 3 suivant l'équation proposée).
Créez donc un calcul réel nommé resolu avec la formule ci-dessous :
si(f2,si(tombejuste,teq'1+2*teq'2,teq1+2*teq2),si(f3,teq3,si(f4,si(tombejuste,teq'1+2*teq'2+3*teq3,teq1+2*teq2+3*teq3),0)))
Notre figure doit aussi contenir un calcul nommé exact qui renvoie 1 si la réponse a été écrite sous la forme x = .. ou …= x et correspond à la première solution sans que son écriture soit nécessairement simplifiée, 2 pour la seconde solution et ainsi de suite.
Si vous voulez que dans ce cas, on ne donne pas d'indication à l'élève lui disant qu'il a presque fini, vous pouvez vous abstenir de définir le calcul exact.
Ici nous allons le définir, ce qui permettra à l'élève de savoir si sa solution est bonne mais refusée parce que non simplifiée sous la forme demandée.
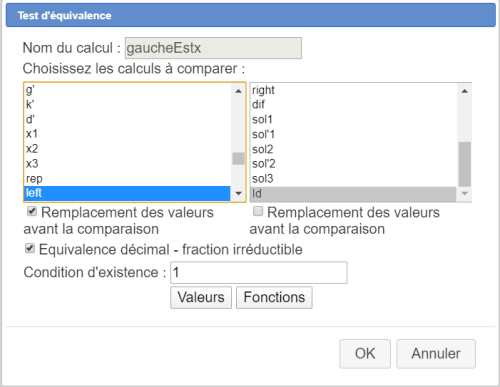
Créez une fonction de la variable réelle x nommée Id avec comme formule :
x
Créez une premier test d'équivalence nommé gaucheEstx comme ci-dessous :
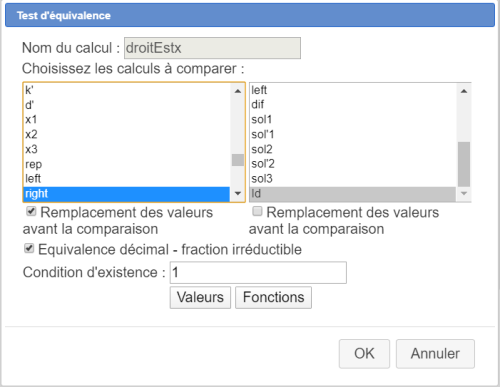
Et un deuxième nommé droitEstx comme ci-dessous :
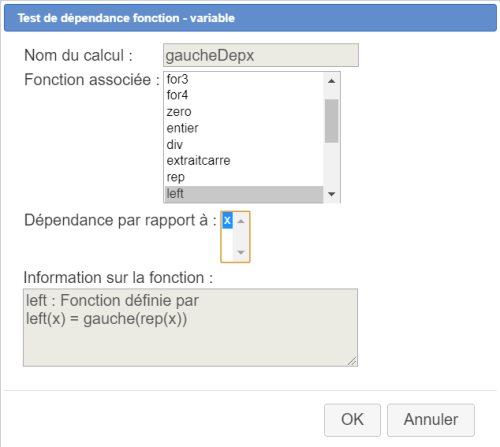
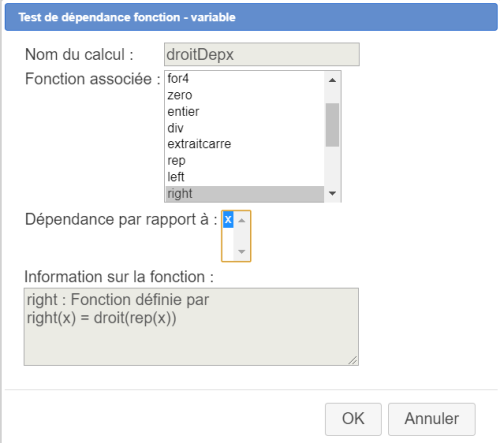
Nous allons maintenant utiliser deux test de dépendance fonction-variable.
Pour cela, cliquez sur l'icône ![]() puis choisissez Test de dépendance fonction-variable dans la liste proposée.
puis choisissez Test de dépendance fonction-variable dans la liste proposée.
Créez les comme ci-dessous :
Créez maintenant les calculs réels suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| xunEstSol | (gaucheEstx&1-droitDepx|droitEstx&1-gaucheDepx)&estSolx1 | Vaut 1 si la formule comprise dans rep est exacte, correspond à la solution n°1 et a été écrite sous la forme x = calcul constant ou calcul constant = x et 0 sinon |
| xdeuxEstSol | (gaucheEstx&1-droitDepx|droitEstx&1-gaucheDepx)&estSolx2 | Vaut 1 si la formule comprise dans rep est exacte, correspond à la solution n°2 et a été écrite sous la forme x = calcul constant ou calcul constant = x et 0 sinon |
| xtroisEstSol | (gaucheEstx&1-droitDepx|droitEstx&1-gaucheDepx)&estSolx3 | Vaut 1 si la formule comprise dans rep est exacte, correspond à la solution n°3 et a été écrite sous la forme x = calcul constant ou calcul constant = x et 0 sinon |
| exact | si(f2,xunEstSol+2*xdeuxEstSol, si(f3,xtroisEstSol,si(f4,xunEstSol+2*xdeuxEstSol,0))) | Renvoie le n° de la solution si une solution est exacte et a été écrite sous la forme x = calcul constant ou calcul constant = x et 0 sinon |
Pour finir nous allons définir quelques calculs et fonctions réelles que nous utiliserons dans l'affichage LaTeX qui servira pour la correction :
Calculs à créer :
| Nom du calcul | Formule |
|---|---|
| k“ | divmaxp(a',2) |
| q” | a'/k“^2 |
| denomsimplif | 1-zero(k”-1) |
| denomestcarre | zero(q“-1) |
| nd | b'*a' |
| dd | a'^2 |
Fonctions numériques réelles à créer :
| Nom de la fonction | Variable | Formule |
|---|---|---|
| form1 | x | a*x^2>=0 |
| form2 | x | a*x^2+b>=b |
| form3 | x | x^2=b'/a' |
| form4 | x | x=sqrt(b'/a') |
| form'4 | x | x=-sqrt(b'/a') |
| form5 | x | x=sqrt(nd/dd) |
| form'5 | x | x=-sqrt(nd/dd) |
| form6 | x | x=sqrt(b')/(k”*sqrt(q“)) |
| form'6 | x | x=-sqrt(b')/(k”*sqrt(q“)) |
| forfact3 | x | x*(a'*x^2+b')=0 |
| forfact4 | x | x*(a'*x^2-b')=0 |
Enfin, utilisez l'outil ![]() pour créer au-dessous des précédents un affichage LaTeX libre dont le code LaTeX est :
pour créer au-dessous des précédents un affichage LaTeX libre dont le code LaTeX est :
\begin{array}{l}
\If{f1}
{
\text{Pour tout réel $x$, $x²\ge0$ donc $\ForSimp{form1}$ donc $\ForSimp{form2}$}
\\ \text{L'équation $\ForSimp{for1}$ n'a donc pas de solution.}
}
{
\If{f2}
{
\text{$\ForSimp{for2}\Leftrightarrow \ForSimp{form3} \Leftrightarrow \ForSimp{form'4}$ ou $\ForSimp{form4}$}
\If{tombejuste}
{
\\\text{$\ForSimp{for2}\Leftrightarrow \ForSimp{sol'2}$ ou $\ForSimp{sol'1}$}
}
{
\If{denomestcarre}
{
\\ \text{$\ForSimp{for2}\Leftrightarrow \ForSimp{sol2}$ ou $\ForSimp{sol1}$}
}
{
\If{denomsimplif}
{
\\ \text{$\ForSimp{for2}\Leftrightarrow \ForSimp{form'6}$ ou $\ForSimp{form6}$}
\\ \text{En multipliant numérateur et dénominateur par $\sqrt{\Val{q"}}$ :}
\\ \text{$\ForSimp{for2}\Leftrightarrow \ForSimp{sol2}$ ou$\ForSimp{sol1}$}
}
{
\\ \text{$\ForSimp{for2}\Leftrightarrow \ForSimp{form'5}$ ou $\ForSimp{form5}$}
\\ \text{$\ForSimp{for2}\Leftrightarrow \ForSimp{sol2}$ ou $\ForSimp{sol1}$}
}
}
}
}
{
\If{f3}
{
\\ \text{$\ForSimp{for3} \Leftrightarrow \ForSimp{forfact3}$}
\\ \text{$\ForSimp{for3} \Leftrightarrow x=0$ ou $\ForSimp{for1}$}
\\ \text{Pour tout réel $x$, $x²\ge0$ donc $\ForSimp{form1}$ donc $\ForSimp{form2}$}
\\ \text{Donc la seule solution de l'équation est $x=0$}.
}
{
\\ \text{$\ForSimp{for4} \Leftrightarrow \ForSimp{forfact4}$}
\\ \text{$\ForSimp{for4}\Leftrightarrow x= 0$ ou $\ForSimp{form3} \Leftrightarrow x=0 $ ou $\ForSimp{form'4}$ ou $\ForSimp{form4}$}
\If{tombejuste}
{
\\\text{$\ForSimp{for4}\Leftrightarrow x=0 $ ou $\ForSimp{sol'2}$ ou $\ForSimp{sol'1}$}
}
{
\If{denomestcarre}
{
\\ \text{$\ForSimp{for4}\Leftrightarrow x=0$ ou $\ForSimp{sol2}$ ou$\ForSimp{sol1}$}
}
{
\If{denomsimplif}
{
\\ \text{$\ForSimp{for4}\Leftrightarrow x=0$ ou $\ForSimp{form'6}$ ou $\ForSimp{form6}$}
\\ \text{En multipliant numérateur et dénominateur des solutions non nulles par $\sqrt{\Val{q"}}$ :}
\\ \text{$\ForSimp{for4}\Leftrightarrow x=0$ ou $\ForSimp{sol2}$ ou$\ForSimp{sol1}$}
}
{
\\ \text{$\ForSimp{for4}\Leftrightarrow x=0$ ou $ \ForSimp{form'5}$ ou $\ForSimp{form5}$}
\\ \text{$\ForSimp{for2}\Leftrightarrow x=0$ ou $\ForSimp{sol2}$ ou $\ForSimp{sol1}$}
}
}
}
}
}
}
\\
\end{array}
Pour que cet affichage de solution soit affiché par la ressource et non par la figure MathGraph32, nous devons lui affecter le tag solution.
Pour cela, utiliser l'outil ![]() de la barre supérieure, sélectionner dans la liste le dernier élément qui est cet affichage LaTeX, cliquez sur le bouton Changer le tag et entrez comme tag :
de la barre supérieure, sélectionner dans la liste le dernier élément qui est cet affichage LaTeX, cliquez sur le bouton Changer le tag et entrez comme tag :
solution
Cet affichage LaTeX renvoie un tableau dont chaque ligne est un \text qui contient ce qui sera affiché dans les lignes correspondantes lors de la solution.
Notre figure est prête pour créer notre ressource. Elle ne sera pas affichée et servira juste à fournir les éléments nécessaires.
Rappelons quels étaient ici les éléments nécessaires, autres que les premiers calculs :
- Un affichage LaTeX (le premier de la figure) renvoyant le code LaTeX de l'équation à résoudre)
- Une fonction nommée rep de la variable x (dans d'autres exercices ce pourrait être une fonction de deux ou trois variables).
- Un calcul nommé nbSol contenant le nombre de solutions
- Des calculs nommés racine1, racine2, racine3 (Ici 3 calculs car la valeur maxi de nbSol est 3) qui renvoient 1 si la solution correspondante est solution de l'équation contenue dans rep.
- Un calcul nommé resolu qui renvoie le numéro de la solution si celle-ci a été donnée sous une forme finale et 0 sinon.
- Un calcul nommé exact qui renvoie le numéro de la solution si celle-ci a été donnée sous une exacte mais non nécessairement finale et 0 sinon
- Un affichage LaTeX de tag solution renvoyant la solution.
Etape 2 : Création de notre ressource dans LaboMep
Connectez vous à LaboMep avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).
Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez par exemple Résoudre une équation.
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez les cases seconde et première.
Dans les champs Résumé et Description, entrez Demande de résoudre une équation de la forme ax²+b=0 ou ax²-b=0 ou ax^3+bx = 0 ou ax^3-bx = 0..
En bas de la page, cliquez sur Créer la ressource.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour J3P.
Ensuite faites glisser Exercice de résolution d'équation dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ Titre entrez ce qui suit :
Résoudre une équation
Dans le champ nbrepetitions entrez la valeur 4.
Ouvrez la figure principale depuis l'endroit où vous l'aviez sauvegardée et utilisez l'icône ![]() d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
Collez ce code Base 64 dans le champ fig.
Il serait possible d'afficher sous les consignes notre figure MathGraph32 et dans ce cas nous devrions entrer la largeur et la hauteur en pixels comme paramètres width et height mais ici notre figure ne sert qu'à fournir ce qui sera affiché, aussi bien lors des questions que lors de la correction.
Nous allons donc entrer 0 comme paramètres width et height.
Dans le champ width entrez 0 (Largeur en pixels de la figure principale).
Dans le champ height entrez 0 (Hauteur en pixels de la figure principale).
Dans le champ param entrez abf ( ce sont les noms des calculs qui pourront être imposés lors de la personnalisation de notre ressource).
Dans le champ nbEssais entrez 6 (C'est le nombre d'essais maximum pour résoudre les équations progressivement).
Dans le champ nbLatex, laissez la valeur 1 : nous avons un seul affichage LaTeX à récupérer pour la consigne.
Dans le champ charset entrez :
x0123456789,.()\^\+\-\*\/()=
Laissez le paramètre simplifier à true.
Ce sont les caractères utilisables dans les champs d'édition de résolution. Certains sont précédés d'un \ car il s'agit en fait d'une expression régulière. Quand vous avez un doute sur un caractère, préfixes-le d'un \.
Vous pouvez laisser ce qu'il y a par défaut dans les champs consigneNbSol0 et consigneNbSol1.
Dans le champ consigne1, entrez :
On veut résoudre dans $\R$ l'équation $£a$.
Dans le champ consigne2, entrez :
L'équation $£a$ admet une ou plusieurs solutions.</br> Entrer ci-dessous la ou les solutions sous la forme $x$ = ... ou ...= $x$ séparées par des ; s'il y en a plusieurs.
Dans le champ consigne3, laissez :
</br>Chaque solution doit être donnée sous la forme la plus simple possible (fraction irréductible, entier ou décimal).
Cette ligne consigne3 n'est affichée que si le paramètre simplifier est à true.
Dans le champ consigne4, laissez :
</br>On peut aussi entrer des équations séparées par des ; pour résoudre progressivement.
Dans le champ consigne5, laissez :
</br>Appuyer sur le bouton <B>OK</B> pour valider la réponse.
Dans le champ nomSolutions laissez solution (on pourrait par exemple utiliser le mot racine).
Cochez les cases true pour btnFrac, btnPuis, btnRac correspondant disponibles dans l'éditeur. Cochez false pour les autres boutons.
Dans le champ InfoParam entrez :
Résolution de ax²+b = 0 (si f = 1) ou ax²-b = 0 (si f = 2) ou ax^3+bx = 0 (si f=3) ou ax^3-bx=0 (si f =4). a et b doivent être des entiers strictement positifs et premiers entre eux.
Ainsi les utilisateurs de la ressource qui voudraient la personnaliser sauront quel est le rôle des paramètres a, b et f. Les autres ne servent pas.
Ici nous laissons tous ces paramètres à random pour qu'ils soient choisis aléatoirement comme nous l'avons prévu.
Vous pouvez maintenant valider la boîte de dialogue de choix des paramètres.
Ensuite cliquez en bas sur le bouton Enregistrer pour enregistrer votre ressource.
Si vous voulez maintenant tester votre ressource, fermez d’abord l’onglet Résoudre une équation puis, dans Mes Ressources, faites un clic droit sur la ressource.
Vous pouvez maintenant tester la ressource.
Quelques compléments
Dans certains cas il peut être utile d'afficher la figure. Il faut alors renseigner les paramètres width et height (largeur et hauteur de la figure en pixels).
Il est possible de mettre le paramètre simplifier à false.
Dans ce cas la consigne contenue dans la paramètre consigne3 ne sera pas affichée et toute solution exacte sera considérée comme bonne du moment qu'elle est écrire sous la forme x = … ou … = x sans être nécessairement simplifiée.