Table des matières
Tableau de signes et résolution d'inéquation
Nous désirons créer une ressource de calcul demandant d'abord de remplir un tableau de signes puis de résoudre une inéquation analogue à cet exercice : https://bibliotheque.sesamath.net/public/voir/64818e50498f2e6972d9fcbf
Pour créer cette ressource vous pouvez utiliser MathGraph32 dans sa version en ligne.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
Etape 1 : Création de la figure MathGraph
Commencez par créer la figure mathgraph.
Si vous désirez sauter ce qui suit vous pouvez utiliser le code Base 64 de la figure ci-dessous et, dans MathGraph32, utiliser l'icône ![]() puis choisir Figure par code Base 64.
puis choisir Figure par code Base 64.
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcvb6#gEA#wEAAAAAAAAAAAUeAAACygAAAQEAAAAAAAAAAQAAAUX#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAPQ1ZhcmlhYmxlQm9ybmVlAP####8AA2NvcgAAAAAAAAAAAAAAAAAAAAA#8AAAAAAAAD#wAAAAAAAAAAABMAABMQABMf####8AAAABAAdDQ2FsY3VsAP####8AB3RhYmxlYXUAATEAAAABP#AAAAAAAAAAAAADAP####8ABnJheXBpeAABNgAAAAFAGAAAAAAAAAAAAAMA#####wAIbmJFdGFwZXMAATIAAAABQAAAAAAAAAAAAAADAP####8ADWV0YXBlSW50ZXJuZTEAATEAAAABP#AAAAAAAAAAAAADAP####8ADWV0YXBlUmVzSW5lcTIAATEAAAABP#AAAAAAAAAAAAADAP####8ABW5idmFyAAE1AAAAAUAUAAAAAAAAAAAAAwD#####AAZuYmNhczEAATgAAAABQCAAAAAAAAAAAAADAP####8ABm5iY2FzMgABMgAAAAFAAAAAAAAAAAAAAAMA#####wAGbmJjYXMzAAE4AAAAAUAgAAAAAAAAAAAAAwD#####AAZuYmNhczQAATIAAAABQAAAAAAAAAAAAAADAP####8ABm5iY2FzNQABMgAAAAFAAAAAAAAAAAAAAAMA#####wACcjEAE2ludChyYW5kKDApKm5iY2FzMSn#####AAAAAgAJQ0ZvbmN0aW9uAv####8AAAABAApDT3BlcmF0aW9uAgAAAAQRAAAAAQAAAAAAAAAAP91hdPUmrfz#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAACAAAAAMA#####wACcjIAE2ludChyYW5kKDApKm5iY2FzMikAAAAEAgAAAAUCAAAABBEAAAABAAAAAAAAAAA#xFGvzanwOAAAAAYAAAAJAAAAAwD#####AAJyMwATaW50KHJhbmQoMCkqbmJjYXMzKQAAAAQCAAAABQIAAAAEEQAAAAEAAAAAAAAAAD#Yh#Tz5+OIAAAABgAAAAoAAAADAP####8AAnI0ABNpbnQocmFuZCgwKSpuYmNhczQpAAAABAIAAAAFAgAAAAQRAAAAAQAAAAAAAAAAP+FD2hwWhZIAAAAGAAAACwAAAAMA#####wACcjUAE2ludChyYW5kKDApKm5iY2FzNSkAAAAEAgAAAAUCAAAABBEAAAABAAAAAAAAAAA#289#w55EAAAAAAYAAAAMAAAAAwD#####AAJhMQAEcjErMgAAAAUAAAAABgAAAA0AAAABQAAAAAAAAAAAAAADAP####8AAmIxAARyMysxAAAABQAAAAAGAAAADwAAAAE#8AAAAAAAAAAAAAMA#####wAFc2lnbmEABygtMSlecjL#####AAAAAQAKQ1B1aXNzYW5jZf####8AAAABAAxDTW9pbnNVbmFpcmUAAAABP#AAAAAAAAAAAAAGAAAADgAAAAMA#####wAFc2lnbmIABygtMSlecjQAAAAHAAAACAAAAAE#8AAAAAAAAAAAAAYAAAAQAAAAAwD#####AANzdXAABHI1PTAAAAAFCAAAAAYAAAARAAAAAQAAAAAAAAAAAAAAAwD#####AAFhAAhzaWduYSphMQAAAAUCAAAABgAAABQAAAAGAAAAEgAAAAMA#####wABYgAIc2lnbmIqYjEAAAAFAgAAAAYAAAAVAAAABgAAABMAAAADAP####8ACGFic2FkaWYxAAlhYnMoYSk8PjEAAAAFCQAAAAQAAAAABgAAABcAAAABP#AAAAAAAAAAAAADAP####8AAWcAE3BnY2QoYWJzKGEpLGFicyhiKSn#####AAAAAQANQ0ZvbmN0aW9uMlZhcgIAAAAEAAAAAAYAAAAXAAAABAAAAAAGAAAAGAAAAAMA#####wAFZ2RpZjEABGc8PjEAAAAFCQAAAAYAAAAaAAAAAT#wAAAAAAAAAAAAAwD#####AAJhJwADYS9nAAAABQMAAAAGAAAAFwAAAAYAAAAaAAAAAwD#####AAJiJwADYi9nAAAABQMAAAAGAAAAGAAAAAYAAAAaAAAAAwD#####AANpbmYABTEtc3VwAAAABQEAAAABP#AAAAAAAAAAAAAGAAAAFgAAAAMA#####wACeDAABi1iJy9hJwAAAAgAAAAFAwAAAAYAAAAdAAAABgAAABwAAAADAP####8ABnJhY3BvcwAEeDA+MAAAAAUFAAAABgAAAB8AAAABAAAAAAAAAAAAAAADAP####8ABnJhY25lZwAIMS1yYWNwb3MAAAAFAQAAAAE#8AAAAAAAAAAAAAYAAAAgAAAAAwD#####AARhcG9zAANhPjAAAAAFBQAAAAYAAAAXAAAAAQAAAAAAAAAAAAAAAwD#####AARhbmVnAAYxLWFwb3MAAAAFAQAAAAE#8AAAAAAAAAAAAAYAAAAiAAAAAwD#####AAR6ZXJvAAEwAAAAAQAAAAAAAAAA#####wAAAAEABUNGb25jAP####8AAXUABWEqeCtiAAAABQAAAAAFAgAAAAYAAAAX#####wAAAAIAEUNWYXJpYWJsZUZvcm1lbGxlAAAAAAAAAAYAAAAYAAF4AAAACgD#####AAFmAAl4LyhhKngrYikAAAAFAwAAAAsAAAAAAAAABQAAAAAFAgAAAAYAAAAXAAAACwAAAAAAAAAGAAAAGAABeAAAAAMA#####wAJcmVwSW50MTExAAd0YWJsZWF1AAAABgAAAAIAAAADAP####8ACXJlcEludDEyMQAHdGFibGVhdQAAAAYAAAAC#####wAAAAQAEENUZXN0RXF1aXZhbGVuY2UA#####wAGdGVxeDAxAAAAHwAAACcBAAAAAAE#8AAAAAAAAAEBAQAAAAwA#####wAIdGVxemVybzEAAAAkAAAAJwEAAAAAAT#wAAAAAAAAAQEBAAAADAD#####AAZ0ZXF4MDIAAAAfAAAAKAEAAAAAAT#wAAAAAAAAAQEBAAAADAD#####AAh0ZXF6ZXJvMgAAACQAAAAoAQAAAAABP#AAAAAAAAABAQH#####AAAAAQAKQ1BvaW50QmFzZQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABQDMAAAAAAABAL64UeuFHsP####8AAAABABRDRHJvaXRlRGlyZWN0aW9uRml4ZQD#####AQAAAAEQAAABAAAAAQAAAC0BP#AAAAAAAAD#####AAAAAQAPQ1BvaW50TGllRHJvaXRlAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAFAWgAAAAAAAAAAAC4AAAAPAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAFAggAAAAAAAAAAAC4AAAAOAP####8BAAAAARAAAAEAAAABAAAALQA#8AAAAAAAAAAAAA8A#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAUBIAAAAAAAAAAAAMf####8AAAABAAxDVHJhbnNsYXRpb24A#####wAAAC0AAAAy#####wAAAAEAC0NQb2ludEltYWdlAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAADIAAAAz#####wAAAAEADUNEZW1pRHJvaXRlT0EA#####wEAAAAADQAAAQAAAAEAAAAyAAAANAAAAA8A#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAT#tVVVVVVVTAAAANQAAABEA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAANgAAADMAAAASAP####8BAAAAAA0AAAEAAAABAAAANgAAADcAAAAPAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAE#7AAAAAAABQAAADgAAAARAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAADkAAAAzAAAAEgD#####AQAAAAANAAABAAAAAQAAADkAAAA6AAAADwD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABP#hVVVVVVVUAAAA7#####wAAAAEACENTZWdtZW50AP####8AAAAAABAAAAEAAAABAAAALQAAADwAAAAQAP####8AAAAtAAAAMAAAABEA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAPAAAAD4AAAAQAP####8AAAAtAAAAPAAAABEA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAALwAAAEAAAAATAP####8AAAAAABAAAAEAAAABAAAAPAAAAD8AAAATAP####8AAAAAABAAAAEAAAABAAAAMAAAAD8AAAATAP####8AAAAAABAAAAEAAAABAAAALQAAADAAAAARAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAADIAAAA+AAAAEwD#####AAAAAAAQAAABAAAAAQAAADIAAABFAAAAEwD#####AAAAAAAQAAABAAAAAQAAAC8AAABBAAAAEQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAA2AAAAPgAAABEA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAOQAAAD4AAAATAP####8AAAAAABAAAAEAAAABAAAANgAAAEj#####AAAAAQAQQ0ludERyb2l0ZURyb2l0ZQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABGAAAAR#####8AAAABAAtDSG9tb3RoZXRpZQD#####AAAASwAAAAUDAAAAAT#wAAAAAAAAAAAAAUAIAAAAAAAAAAAAEQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABFAAAATAAAABMA#####wAAAAAAEAAAAQAAAAEAAAA5AAAASQAAABQA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAARwAAAEoAAAAUAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEcAAABOAAAAEAD#####AAAASwAAAE0AAAARAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAE0AAABRAAAAEAD#####AAAAMgAAADYAAAARAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAE0AAABTAAAAEQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABSAAAAU#####8AAAABAAdDTWlsaWV1AP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAADIAAAAvAAAAFgD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAA2AAAASwAAABYA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAATwAAAE0AAAAWAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFQAAABSAAAAFgD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABVAAAARQAAABAA#####wAAADYAAAA5AAAAEQD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABUAAAAWwAAABEA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAVQAAAFsAAAAQAP####8AAAA5AAAAPAAAABEA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAXAAAAF4AAAARAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAF0AAABeAAAAFgD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAA5AAAATwAAABYA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAUAAAAFQAAAAWAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFwAAABVAAAAFgD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABdAAAASAAAABYA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAPAAAAFAAAAAWAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEEAAABcAAAAFgD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABfAAAAXQAAABYA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAYAAAAEkAAAAWAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAE0AAABUAAAAFgD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABSAAAAVQAAABYA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAVAAAAFwAAAAWAP####8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFUAAABdAAAAFgD#####AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABcAAAAXwAAABYA#####wEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAXQAAAGD#####AAAAAgAGQ0xhdGV4AP####8AAAAAAEAUAAAAAAAAwBAAAAAAAAAAAAAAAEsQAAAAAAAAAAAAAgAAAAEAAAAAAAAAAAAHLVxpbmZ0eQAAABcA#####wAAAAAAwCAAAAAAAADAEAAAAAAAAAAAAAAARRAAAAAAAAIAAAACAAAAAQAAAAAAAAAAAAcrXGluZnR5AAAAFwD#####AAAAAABACAAAAAAAAEAkAAAAAAAAAAAAAABWEAAAAAAAAQAAAAEAAAABAAAAAAAAAAAAAXgAAAAXAP####8AAAAAAQAAAAAAVxAAAAAAAAEAAAABAAAAAQAAAAAAAAAAAAF4AAAAFwD#####AAAAAAEAAAAAAGEQAAAAAAABAAAAAQAAAAEAAAAAAAAAAAALXEZvclNpbXB7dX0AAAAXAP####8AAAAAAQAAAAAAZRAAAAAAAAEAAAABAAAAAQAAAAAAAAAAAAtcRm9yU2ltcHtmfQAAABcA#####wAAAAAAAAAAAAAAAADAEAAAAAAAAAAPZm9ybXVsYWlyZUludDExAAAATRAAAAAAAAEAAAACAAAAAQAAAAAAAAAAAAxcdGV4dHtlZGl0MX0AAAAXAP####8B#wAAAL#wAAAAAAAAwDoAAAAAAAAACXNvbEludDExMQAAAE0QAAAAAAABAAAAAgAAAAEAAAAAAAAAAAAcXElme3JhY3Bvc317MH17XEZvclNpbXB7eDB9fQAAABcA#####wAAAAAAAAAAAAAAAADACAAAAAAAAAAPZm9ybXVsYWlyZUludDEyAAAAUhAAAAAAAAEAAAACAAAAAQAAAAAAAAAAAAxcdGV4dHtlZGl0MX0AAAAXAP####8B#wAAAMAAAAAAAAAAwDkAAAAAAAAACXNvbEludDEyMQAAAFIQAAAAAAABAAAAAgAAAAEAAAAAAAAAAAAcXElme3JhY3Bvc317XEZvclNpbXB7eDB9fXswfQAAABcA#####wAAAAABAA9mb3JtdWxhaXJlSW50MTMAAABYGgAAAAAAAQAAAAEAAAABAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAABcA#####wH#AAAAwDkAAAAAAAAAAAAAAAAAAAAKbGlzdEludDEzMQAAAFgNAAAAAAACAAAAAQAAAAEAAAAAAAAAAAA+XGJlZ2lue2FycmF5fXtsfQpcdGV4dHsrfSAKXFwgXHRleHR7LX0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAAXAP####8AAAAAAQAPZm9ybXVsYWlyZUludDE0AAAAaRoAAAAAAAEAAAABAAAAAQAAAAAAAAAAAAxcdGV4dHtsaXN0MX0AAAAXAP####8B#wAAAMA5AAAAAAAAQAAAAAAAAAAACmxpc3RJbnQxNDEAAABpDQAAAAAAAgAAAAEAAAABAAAAAAAAAAAAP1xiZWdpbnthcnJheX17bH0KXHRleHR7fH0gClxcIFx0ZXh0e3x8fQpcXCBcdGV4dHswfQpcZW5ke2FycmF5fQAAABcA#####wAAAAABAA9mb3JtdWxhaXJlSW50MTUAAABZGgAAAAAAAQAAAAEAAAABAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAABcA#####wH#AAAAwDcAAAAAAAAAAAAAAAAAAAAKbGlzdEludDE1MQAAAFkNAAAAAAACAAAAAQAAAAEAAAAAAAAAAAA+XGJlZ2lue2FycmF5fXtsfQpcdGV4dHsrfSAKXFwgXHRleHR7LX0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAAXAP####8AAAAAAQAPZm9ybXVsYWlyZUludDE2AAAAahoAAAAAAAEAAAABAAAAAQAAAAAAAAAAAAxcdGV4dHtsaXN0MX0AAAAXAP####8B#wAAAMA7AAAAAAAAAAAAAAAAAAAACmxpc3RJbnQxNjEAAABqDQAAAAAAAgAAAAEAAAABAAAAAAAAAAAAP1xiZWdpbnthcnJheX17bH0KXHRleHR7fH0gClxcIFx0ZXh0e3x8fQpcXCBcdGV4dHswfQpcZW5ke2FycmF5fQAAABcA#####wAAAAABAA9mb3JtdWxhaXJlSW50MTcAAABaGgAAAAAAAQAAAAEAAAABAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAABcA#####wH#AAAAwDkAAAAAAAC#8AAAAAAAAAAKbGlzdEludDE3MQAAAFoNAAAAAAACAAAAAQAAAAEAAAAAAAAAAAA+XGJlZ2lue2FycmF5fXtsfQpcdGV4dHsrfSAKXFwgXHRleHR7LX0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAAXAP####8AAAAAAQAPZm9ybXVsYWlyZUludDE4AAAAYhoAAAAAAAEAAAABAAAAAQAAAAAAAAAAAAxcdGV4dHtsaXN0MX0AAAAXAP####8B#wAAAMA6AAAAAAAAQAgAAAAAAAAACmxpc3RJbnQxODEAAABiDQAAAAAAAgAAAAEAAAABAAAAAAAAAAAAPlxiZWdpbnthcnJheX17bH0KXHRleHR7K30gClxcIFx0ZXh0ey19ClxcIFx0ZXh0ezB9ClxlbmR7YXJyYXl9AAAAFwD#####AAAAAAEAD2Zvcm11bGFpcmVJbnQxOQAAAGsaAAAAAAABAAAAAQAAAAEAAAAAAAAAAAAMXHRleHR7bGlzdDF9AAAAFwD#####Af8AAADAOgAAAAAAAD#wAAAAAAAAAApsaXN0SW50MTkxAAAAaw0AAAAAAAIAAAABAAAAAQAAAAAAAAAAAD9cYmVnaW57YXJyYXl9e2x9Clx0ZXh0e3x9IApcXCBcdGV4dHt8fH0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAAXAP####8AAAAAAQAQZm9ybXVsYWlyZUludDExMAAAAGMaAAAAAAABAAAAAQAAAAEAAAAAAAAAAAAMXHRleHR7bGlzdDF9AAAAFwD#####Af8AAADAOgAAAAAAAAAAAAAAAAAAAAtsaXN0SW50MTEwMQAAAGMNAAAAAAACAAAAAQAAAAEAAAAAAAAAAAA+XGJlZ2lue2FycmF5fXtsfQpcdGV4dHsrfSAKXFwgXHRleHR7LX0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAAXAP####8AAAAAAQAQZm9ybXVsYWlyZUludDExMQAAAGwaAAAAAAABAAAAAQAAAAEAAAAAAAAAAAAMXHRleHR7bGlzdDF9AAAAFwD#####Af8AAADAOQAAAAAAAAAAAAAAAAAAAAtsaXN0SW50MTExMQAAAGwNAAAAAAACAAAAAQAAAAEAAAAAAAAAAAA#XGJlZ2lue2FycmF5fXtsfQpcdGV4dHt8fSAKXFwgXHRleHR7fHx9ClxcIFx0ZXh0ezB9ClxlbmR7YXJyYXl9AAAAFwD#####AAAAAAEAEGZvcm11bGFpcmVJbnQxMTIAAABkGgAAAAAAAQAAAAEAAAABAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAABcA#####wH#AAAAwDsAAAAAAAAAAAAAAAAAAAALbGlzdEludDExMjEAAABkDQAAAAAAAgAAAAEAAAABAAAAAAAAAAAAPlxiZWdpbnthcnJheX17bH0KXHRleHR7K30gClxcIFx0ZXh0ey19ClxcIFx0ZXh0ezB9ClxlbmR7YXJyYXl9AAAAFwD#####AAAAAAEAEGZvcm11bGFpcmVJbnQxMTMAAABmGgAAAAAAAQAAAAEAAAABAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAABcA#####wH#AAAAwDoAAAAAAAC#8AAAAAAAAAALbGlzdEludDExMzEAAABmDQAAAAAAAgAAAAEAAAABAAAAAAAAAAAAPlxiZWdpbnthcnJheX17bH0KXHRleHR7K30gClxcIFx0ZXh0ey19ClxcIFx0ZXh0ezB9ClxlbmR7YXJyYXl9AAAAFwD#####AAAAAAEAEGZvcm11bGFpcmVJbnQxMTQAAABtGgAAAAAAAQAAAAEAAAABAAAAAAAAAAAADFx0ZXh0e2xpc3QxfQAAABcA#####wH#AAAAwDcAAAAAAADACAAAAAAAAAALbGlzdEludDExNDEAAABtDQAAAAAAAgAAAAEAAAABAAAAAAAAAAAAP1xiZWdpbnthcnJheX17bH0KXHRleHR7fH0gClxcIFx0ZXh0e3x8fQpcXCBcdGV4dHswfQpcZW5ke2FycmF5fQAAABcA#####wAAAAABABBmb3JtdWxhaXJlSW50MTE1AAAAZxoAAAAAAAEAAAABAAAAAQAAAAAAAAAAAAxcdGV4dHtsaXN0MX0AAAAXAP####8B#wAAAMA3AAAAAAAAv#AAAAAAAAAAC2xpc3RJbnQxMTUxAAAAZw0AAAAAAAIAAAABAAAAAQAAAAAAAAAAAD5cYmVnaW57YXJyYXl9e2x9Clx0ZXh0eyt9IApcXCBcdGV4dHstfQpcXCBcdGV4dHswfQpcZW5ke2FycmF5fQAAABcA#####wAAAAABABBmb3JtdWxhaXJlSW50MTE2AAAAbhoAAAAAAAEAAAABAAAAAQAAAAAAAAAAAAxcdGV4dHtsaXN0MX0AAAAXAP####8B#wAAAMA4AAAAAAAAP#AAAAAAAAAAC2xpc3RJbnQxMTYxAAAAbg0AAAAAAAIAAAABAAAAAQAAAAAAAAAAAD9cYmVnaW57YXJyYXl9e2x9Clx0ZXh0e3x9IApcXCBcdGV4dHt8fH0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAAXAP####8AAAAAAQAQZm9ybXVsYWlyZUludDExNwAAAGgaAAAAAAABAAAAAQAAAAEAAAAAAAAAAAAMXHRleHR7bGlzdDF9AAAAFwD#####Af8AAADAOgAAAAAAAAAAAAAAAAAAAAtsaXN0SW50MTE3MQAAAGgNAAAAAAACAAAAAQAAAAEAAAAAAAAAAAA+XGJlZ2lue2FycmF5fXtsfQpcdGV4dHsrfSAKXFwgXHRleHR7LX0KXFwgXHRleHR7MH0KXGVuZHthcnJheX0AAAADAP####8ADHJlc29sdUludDExMQAac2kocmFjcG9zLHRlcXplcm8xLHRlcXgwMSn#####AAAAAQANQ0ZvbmN0aW9uM1ZhcgAAAAAGAAAAIAAAAAYAAAAqAAAABgAAACkAAAADAP####8ADHJlc29sdUludDEyMQAac2kocmFjcG9zLHRlcXgwMix0ZXF6ZXJvMikAAAAYAAAAAAYAAAAgAAAABgAAACsAAAAGAAAALAAAAAMA#####wANcmVzTGlzdEludDEzMQABMgAAAAFAAAAAAAAAAAAAAAMA#####wANcmVzTGlzdEludDE0MQAOc2kocmFjcG9zLDMsMSkAAAAYAAAAAAYAAAAgAAAAAUAIAAAAAAAAAAAAAT#wAAAAAAAAAAAAAwD#####AA1yZXNMaXN0SW50MTUxAA5zaShyYWNwb3MsMSwyKQAAABgAAAAABgAAACAAAAABP#AAAAAAAAAAAAABQAAAAAAAAAAAAAADAP####8ADXJlc0xpc3RJbnQxNjEADnNpKHJhY3BvcywxLDMpAAAAGAAAAAAGAAAAIAAAAAE#8AAAAAAAAAAAAAFACAAAAAAAAAAAAAMA#####wANcmVzTGlzdEludDE3MQABMQAAAAE#8AAAAAAAAAAAAAMA#####wANcmVzTGlzdEludDE4MQAMc2koYXBvcywyLDEpAAAAGAAAAAAGAAAAIgAAAAFAAAAAAAAAAAAAAAE#8AAAAAAAAAAAAAMA#####wANcmVzTGlzdEludDE5MQAOc2kocmFjcG9zLDEsMykAAAAYAAAAAAYAAAAgAAAAAT#wAAAAAAAAAAAAAUAIAAAAAAAAAAAAAwD#####AA5yZXNMaXN0SW50MTEwMQAkc2kocmFjcG9zLHNpKGFwb3MsMiwxKSxzaShhcG9zLDEsMikpAAAAGAAAAAAGAAAAIAAAABgAAAAABgAAACIAAAABQAAAAAAAAAAAAAABP#AAAAAAAAAAAAAYAAAAAAYAAAAiAAAAAT#wAAAAAAAAAAAAAUAAAAAAAAAAAAAAAwD#####AA5yZXNMaXN0SW50MTExMQAOc2kocmFjcG9zLDMsMSkAAAAYAAAAAAYAAAAgAAAAAUAIAAAAAAAAAAAAAT#wAAAAAAAAAAAAAwD#####AA5yZXNMaXN0SW50MTEyMQAMc2koYXBvcywxLDIpAAAAGAAAAAAGAAAAIgAAAAE#8AAAAAAAAAAAAAFAAAAAAAAAAAAAAAMA#####wAOcmVzTGlzdEludDExMzEADHNpKGFwb3MsMSwyKQAAABgAAAAABgAAACIAAAABP#AAAAAAAAAAAAABQAAAAAAAAAAAAAADAP####8ADnJlc0xpc3RJbnQxMTQxAA5zaShyYWNwb3MsMywyKQAAABgAAAAABgAAACAAAAABQAgAAAAAAAAAAAABQAAAAAAAAAAAAAADAP####8ADnJlc0xpc3RJbnQxMTUxAAxzaShhcG9zLDIsMSkAAAAYAAAAAAYAAAAiAAAAAUAAAAAAAAAAAAAAAT#wAAAAAAAAAAAAAwD#####AA5yZXNMaXN0SW50MTE2MQAOc2kocmFjcG9zLDIsMykAAAAYAAAAAAYAAAAgAAAAAUAAAAAAAAAAAAAAAUAIAAAAAAAAAAAAAwD#####AA5yZXNMaXN0SW50MTE3MQAMc2koYXBvcywxLDIpAAAAGAAAAAAGAAAAIgAAAAE#8AAAAAAAAAAAAAFAAAAAAAAAAAAAAAMA#####wADZXBzAA4wLjAwMDAwMDAwMDAwMQAAAAE9cZeZgS3qEQAAAAMA#####wAFeFRlc3QAATAAAAABAAAAAAAAAAAAAAADAP####8ADHRvdXRSZWVsU29sMgABMAAAAAEAAAAAAAAAAAAAAAMA#####wAFdmlkZTIAATAAAAABAAAAAAAAAAAAAAADAP####8AEHBsdXNJbmZTb2x1dGlvbjIAEXN1cCZhcG9zfGluZiZhbmVnAAAABQsAAAAFCgAAAAYAAAAWAAAABgAAACIAAAAFCgAAAAYAAAAeAAAABgAAACMAAAADAP####8AEW1vaW5zSW5mU29sdXRpb24yABFzdXAmYXBvc3xpbmYmYW5lZwAAAAULAAAABQoAAAAGAAAAFgAAAAYAAAAiAAAABQoAAAAGAAAAHgAAAAYAAAAjAAAACgD#####AAl6ZXJvQm9ybmUACmFicyh4KTxlcHMAAAAFBAAAAAQAAAAACwAAAAAAAAAGAAAAqAABeAAAAAoA#####wAEcmVwMgABMAAAAAEAAAAAAAAAAAABeAAAAAoA#####wAOcmVwUG91ckJvcm5lczIAATAAAAABAAAAAAAAAAAAAXgAAAADAP####8AD2VzdEJvcm5lSXNvbGVlMgABMAAAAAEAAAAAAAAAAAAAAAoA#####wAJc29sdXRpb24xAA14PD0wfHg+LWInL2EnAAAABQsAAAAFBgAAAAsAAAAAAAAAAQAAAAAAAAAAAAAABQUAAAALAAAAAAAAAAgAAAAFAwAAAAYAAAAdAAAABgAAABwAAXgAAAAKAP####8ACXNvbHV0aW9uMgANeDwtYicvYSd8eD49MAAAAAULAAAABQQAAAALAAAAAAAAAAgAAAAFAwAAAAYAAAAdAAAABgAAABwAAAAFBwAAAAsAAAAAAAAAAQAAAAAAAAAAAAF4AAAACgD#####AAlzb2x1dGlvbjMADXg+PTAmeDwtYicvYScAAAAFCgAAAAUHAAAACwAAAAAAAAABAAAAAAAAAAAAAAAFBAAAAAsAAAAAAAAACAAAAAUDAAAABgAAAB0AAAAGAAAAHAABeAAAAAoA#####wAJc29sdXRpb240AA14Pi1iJy9hJyZ4PD0wAAAABQoAAAAFBQAAAAsAAAAAAAAACAAAAAUDAAAABgAAAB0AAAAGAAAAHAAAAAUGAAAACwAAAAAAAAABAAAAAAAAAAAAAXgAAAADAP####8ADW5iU29sSXNvbGVlczIAATAAAAABAAAAAAAAAAAAAAADAP####8ADWVzdHNvbElzb2xlZTIAATAAAAABAAAAAAAAAAAAAAADAP####8AD2VzdEJvcm5lRmVybWVlMgASemVyb0Jvcm5lKHhUZXN0LTAp#####wAAAAEADkNBcHBlbEZvbmN0aW9uAAAArgAAAAUBAAAABgAAAKkAAAABAAAAAAAAAAAAAAADAP####8ADGVzdFNvbHV0aW9uMgDNc2koc3VwLHNpKGFwb3Msc2kocmFjcG9zLHNvbHV0aW9uMSh4VGVzdCksc29sdXRpb24yKHhUZXN0KSksc2kocmFjcG9zLHNvbHV0aW9uMyh4VGVzdCksc29sdXRpb240KHhUZXN0KSkpLHNpKGFwb3Msc2kocmFjcG9zLHNvbHV0aW9uMyh4VGVzdCksc29sdXRpb240KHhUZXN0KSksc2kocmFjcG9zLHNvbHV0aW9uMSh4VGVzdCksc29sdXRpb24yKHhUZXN0KSkpKQAAABgAAAAABgAAABYAAAAYAAAAAAYAAAAiAAAAGAAAAAAGAAAAIAAAABkAAACyAAAABgAAAKkAAAAZAAAAswAAAAYAAACpAAAAGAAAAAAGAAAAIAAAABkAAAC0AAAABgAAAKkAAAAZAAAAtQAAAAYAAACpAAAAGAAAAAAGAAAAIgAAABgAAAAABgAAACAAAAAZAAAAtAAAAAYAAACpAAAAGQAAALUAAAAGAAAAqQAAABgAAAAABgAAACAAAAAZAAAAsgAAAAYAAACpAAAAGQAAALMAAAAGAAAAqQAAAAMA#####wAPcmVwQ29udGllbnRTb2wyAN1zaShzdXAmYXBvc3xpbmYmYW5lZyxzaShyYWNwb3MscmVwUG91ckJvcm5lczIoLWVwcykmcmVwUG91ckJvcm5lczIoeDArZXBzKSxyZXBQb3VyQm9ybmVzMih4MC1lcHMpJnJlcFBvdXJCb3JuZXMyKDArZXBzKSksc2kocmFjcG9zLHJlcFBvdXJCb3JuZXMyKDArZXBzKSZyZXBQb3VyQm9ybmVzMih4MC1lcHMpLHJlcFBvdXJCb3JuZXMyKHgwK2VwcykmcmVwUG91ckJvcm5lczIoLWVwcykpKQAAABgAAAAABQsAAAAFCgAAAAYAAAAWAAAABgAAACIAAAAFCgAAAAYAAAAeAAAABgAAACMAAAAYAAAAAAYAAAAgAAAABQoAAAAZAAAAsAAAAAgAAAAGAAAAqAAAABkAAACwAAAABQAAAAAGAAAAHwAAAAYAAACoAAAABQoAAAAZAAAAsAAAAAUBAAAABgAAAB8AAAAGAAAAqAAAABkAAACwAAAABQAAAAABAAAAAAAAAAAAAAAGAAAAqAAAABgAAAAABgAAACAAAAAFCgAAABkAAACwAAAABQAAAAABAAAAAAAAAAAAAAAGAAAAqAAAABkAAACwAAAABQEAAAAGAAAAHwAAAAYAAACoAAAABQoAAAAZAAAAsAAAAAUAAAAABgAAAB8AAAAGAAAAqAAAABkAAACwAAAABQEAAAABAAAAAAAAAAAAAAAGAAAAqAAAAAoA#####wAMZm9uY3Rpb25UZXN0AAEwAAAAAQAAAAAAAAAAAAF4AAAAAwD#####AA5jb250aWVudEJvcm5lMgAgZm9uY3Rpb25UZXN0KDApfGZvbmN0aW9uVGVzdCh4MCkAAAAFCwAAABkAAAC7AAAAAQAAAAAAAAAAAAAAGQAAALsAAAAGAAAAHwAAAAoA#####wARcmVwQm9ybmVzRmVybWVlczIACTAqdGFibGVhdQAAAAUCAAAAAQAAAAAAAAAAAAAABgAAAAIAAXgAAAAMAP####8ABHRlcTEAAACyAAAArwEAAAAAAT#wAAAAAAAAAQEBAAAADAD#####AAR0ZXEyAAAAswAAAK8BAAAAAAE#8AAAAAAAAAEBAQAAAAwA#####wAEdGVxMwAAALQAAACvAQAAAAABP#AAAAAAAAABAQEAAAAMAP####8ABHRlcTQAAAC1AAAArwEAAAAAAT#wAAAAAAAAAQEBAAAAAwD#####AAdyZXNvbHUyAG1zaShzdXAsc2koYXBvcyxzaShyYWNwb3MsdGVxMSx0ZXEyKSxzaShyYWNwb3MsdGVxMyx0ZXE0KSksc2koYXBvcyxzaShyYWNwb3MsdGVxMyx0ZXE0KSxzaShyYWNwb3MsdGVxMSx0ZXEyKSkpAAAAGAAAAAAGAAAAFgAAABgAAAAABgAAACIAAAAYAAAAAAYAAAAgAAAABgAAAL4AAAAGAAAAvwAAABgAAAAABgAAACAAAAAGAAAAwAAAAAYAAADBAAAAGAAAAAAGAAAAIgAAABgAAAAABgAAACAAAAAGAAAAwAAAAAYAAADBAAAAGAAAAAAGAAAAIAAAAAYAAAC+AAAABgAAAL8AAAADAP####8ADnByZXNxdWVSZXNvbHUyAAEwAAAAAQAAAAAAAAAAAAAAFwD#####AQAAAAEAB2Vub25jZTH#####EEA1AAAAAAAAQHNNcKPXCj4AAAAAAAAAAAAAAAAAAQAAAAAAAAAAAUJcYmVnaW57YXJyYXl9e2x9Clx0ZXh0e0xlIGJ1dCBkZSBjZXQgZXhlcmNpY2UgZXN0IGRlIHLDqXNvdWRyZSBsJ2luw6lxdWF0aW9uICRcRm9yU2ltcHtmfVxJZntzdXB9e1xnZX17XGxlfTAkLn0gClxcIFx0ZXh0eyRcdGV4dGNvbG9ye21hcm9vbn17XHRleHR7RGFucyB1biBwcmVtaWVyIHRlbXBzIG9uIGRlbWFuZGUgZGUgcmVtcGxpciBsZSB0YWJsZWF1IGRlIHNpZ25lcyBzdWl2YW50IDp9fSR9ClxcIFx0ZXh0eyhMZXMgdmFsZXVycyBkZSBsYSBwcmVtacOocmUgbGlnbmUgZG9pdmVudCDDqnRyZSBzaW1wbGlmacOpZXMgYXUgbWF4aW11bSl9ClxlbmR7YXJyYXl9AAAACgD#####AARmb3IxAAZhKng9LWIAAAAFCAAAAAUCAAAABgAAABcAAAALAAAAAAAAAAgAAAAGAAAAGAABeAAAAAoA#####wAEZm9yMgAGeD0tYi9hAAAABQgAAAALAAAAAAAAAAgAAAAFAwAAAAYAAAAYAAAABgAAABcAAXgAAAAXAP####8BAAAAAQAHZW5vbmNlMv####8QQDgAAAAAAABAeI1wo9cKPgAAAAAAAAAAAAAAAAABAAAAAAAAAAADG1xiZWdpbnthcnJheX17bH0KXHRleHR7JHUoeCk9XEZvclNpbXB7dX0kIGVzdCBkZSBsYSBmb3JtZSAkYXgrYiQgYXZlYyAkYT1cVmFse2F9JCBldCAkYj1cVmFse2J9JC59ClxcIFx0ZXh0eyR1KHgpPTAgXExlZnRyaWdodGFycm93IFxGb3JTaW1we3V9PTAgXElme2Fic2FkaWYxfXtcTGVmdHJpZ2h0YXJyb3cgXEZvclNpbXB7Zm9yMX0gXElme2dkaWYxfXtcTGVmdHJpZ2h0YXJyb3cgXEZvclNpbXB7Zm9yMn19e319e30gXExlZnRyaWdodGFycm93IHg9XEZvclNpbXB7eDB9JC59ClxcIFx0ZXh0e1F1YW5kICR4JCBlc3QgIsOgIGRyb2l0ZSIgZGUgJFxGb3JTaW1we3gwfSQsICR1KHgpJCBhIGxlIHNpZ25lIGRlICRhPVxWYWx7YX0kIGRvbmMgZXN0IGljaSBcSWZ7YXBvc317cG9zaXRpZn17bsOpZ2F0aWZ9Ln0KXFwgXHRleHR7TGUgcXVvdGllbnQgJFxGb3JTaW1we2Z9JCBzJ2FubnVsZSBwb3VyICR4PTAkIGV0IG4nZXhpc3RlIHBhcyBwb3VyICR4PVxGb3JTaW1we3gwfSQsIHZhbGV1ciBwb3VyIGxhcXVlbGxlIHNvbiBkw6lub21pbmF0ZXVyIHMnYW5udWxlLn0KXFwgXHRleHR7JFx0ZXh0Y29sb3J7bWFyb29ufXtcdGV4dHtBIGwnYWlkZSBkdSB0YWJsZWF1IGRlIHNpZ25lcyBjaS1kZXNzb3VzLCBvbiBkZW1hbmRlIG1haW50ZW5hbnQgZGUgZG9ubmVyfX0kfSAKXFwgXHRleHR7JFx0ZXh0Y29sb3J7bWFyb29ufXtcdGV4dHtsJ2Vuc2VtYmxlIGRlcyBzb2x1dGlvbnMgfVNcdGV4dHsgZGUgbCdpbsOpcXVhdGlvbiB9XEZvclNpbXB7Zn1cSWZ7c3VwfXtcZ2V9e1xsZX0wfSQufQpcZW5ke2FycmF5fQAAABcA#####wEAAAABAAtmb3JtdWxhaXJlMv####8QQIPoAAAAAABAc81wo9cKPgAAAAAAAAAAAAAAAAABAAAAAAAAAAAAElx0ZXh0eyRTJCA9IGVkaXQxfQAAAAMA#####wAEY2FzMQAaKHN1cCZhcG9zfGluZiZhbmVnKSZyYWNwb3MAAAAFCgAAAAULAAAABQoAAAAGAAAAFgAAAAYAAAAiAAAABQoAAAAGAAAAHgAAAAYAAAAjAAAABgAAACAAAAAVAP####8AAAAtAAAABQMAAAABP#AAAAAAAAAAAAAFAgAAAAYAAADJAAAABgAAAAEAAAARAP####8BAAD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAABAAAAAE0AAADKAAAAEQD#####Af8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABSAAAAygAAABEA#####wH#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAXAAAAMoAAAARAP####8B#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAF0AAADK#####wAAAAEAFENJbXBsZW1lbnRhdGlvblByb3RvAP####8AEVNlZ21lbnRTZW1pT3V2ZXJ0AAAACgAAAAMAAAADAAAAAwAAAMsAAABLAAAAEwAAAADPAQAAAAAQAAABAAAAAQAAAMsAAABL#####wAAAAIACUNDZXJjbGVPUgAAAADPAQAAAAAAAAEAAABLAAAABgAAAAMB#####wAAAAEAFkNEcm9pdGVQZXJwZW5kaWN1bGFpcmUAAAAAzwEAAAAAEAAAAQAAAAEAAABLAAAA0P####8AAAABABBDSW50RHJvaXRlQ2VyY2xlAAAAAM8AAADSAAAA0f####8AAAABABBDUG9pbnRMaWVCaXBvaW50AAAAAM8BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAEAAADTAAAAHgAAAADPAQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQACAAAA0#####8AAAABABJDQXJjRGVDZXJjbGVEaXJlY3QBAAAAzwD#AAAAAAACAAAASwAAANUAAADUAAAAHQAAAADPAAAA0AAAANEAAAAeAAAAAM8B#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAIAAADXAAAAEwEAAADPAP8AAAAQAAABAAAAAgAAAMsAAADYAAAAFgAAAADPAf8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAADLAAAAS#####8AAAABABFDU3ltZXRyaWVDZW50cmFsZQAAAADPAAAA2gAAABEBAAAAzwD#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAgAAAAASwAAANsAAAAaAP####8ADVNlZ21lbnRPdXZlcnQAAAALAAAAAwAAAAMAAAADAAAAzAAAAEUAAAATAAAAAN0BAAAAABAAAAEAAAABAAAARQAAAMwAAAAbAAAAAN0BAAAAAAAAAQAAAMwAAAAGAAAAAwEAAAAcAAAAAN0BAAAAABAAAAEAAAABAAAAzAAAAN4AAAAdAAAAAN0AAADgAAAA3wAAAB4AAAAA3QEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAQAAAOEAAAAeAAAAAN0BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAIAAADhAAAAHwEAAADdAP8AAAAAAAIAAADMAAAA4wAAAOIAAAAdAAAAAN0AAADeAAAA3wAAAB4AAAAA3QH#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAgAAAOUAAAAWAAAAAN0B#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAEUAAADMAAAAIAAAAADdAAAA5#####8AAAABABFDQXJjRGVDZXJjbGVJbWFnZQEAAADdAP8AAAAAAAIAAADoAAAA5AAAABEAAAAA3QH#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAA5gAAAOgAAAATAQAAAN0A#wAAABAAAAEAAAACAAAA6gAAAOb#####AAAAAQAJQ1BvbHlnb25lAP####8B##8AAAAAAQAAAAUAAABQAAAAzQAAAF8AAABBAAAAUP####8AAAABABBDU3VyZmFjZVBvbHlnb25lAP####8A##8AAAAAAAAFAAAA7AAAACIA#####wH##wAAAAABAAAABQAAAM4AAABJAAAAPwAAAGAAAADOAAAAIwD#####AP##AAAAAAAABQAAAO4AAAADAP####8ABGNhczIAGihzdXAmYXBvc3xpbmYmYW5lZykmcmFjbmVnAAAABQoAAAAFCwAAAAUKAAAABgAAABYAAAAGAAAAIgAAAAUKAAAABgAAAB4AAAAGAAAAIwAAAAYAAAAhAAAAFQD#####AAAALQAAAAUDAAAAAT#wAAAAAAAAAAAABQIAAAAGAAAA8AAAAAYAAAABAAAAEQD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABNAAAA8QAAABEA#####wH#AP8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAUgAAAPEAAAARAP####8B#wD#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFwAAADxAAAAEQD#####Af8A#wAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABdAAAA8QAAABoA#####wANU2VnbWVudE91dmVydAAAAAsAAAADAAAAAwAAAAMAAADyAAAASwAAABMAAAAA9gEAAAAAEAAAAQAAAAEAAABLAAAA8gAAABsAAAAA9gEAAAAAAAABAAAA8gAAAAYAAAADAQAAABwAAAAA9gEAAAAAEAAAAQAAAAEAAADyAAAA9wAAAB0AAAAA9gAAAPkAAAD4AAAAHgAAAAD2AQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQABAAAA+gAAAB4AAAAA9gEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAgAAAPoAAAAfAQAAAPYA#wAAAAAAAgAAAPIAAAD8AAAA+wAAAB0AAAAA9gAAAPcAAAD4AAAAHgAAAAD2Af8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQACAAAA#gAAABYAAAAA9gH#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAASwAAAPIAAAAgAAAAAPYAAAEAAAAAIQEAAAD2AP8AAAAAAAIAAAEBAAAA#QAAABEAAAAA9gH#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAA#wAAAQEAAAATAQAAAPYA#wAAABAAAAEAAAACAAABAwAAAP8AAAAaAP####8AEVNlZ21lbnRTZW1pT3V2ZXJ0AAAACgAAAAMAAAADAAAAAwAAAPMAAABFAAAAEwAAAAEFAQAAAAAQAAABAAAAAQAAAPMAAABFAAAAGwAAAAEFAQAAAAAAAAEAAABFAAAABgAAAAMBAAAAHAAAAAEFAQAAAAAQAAABAAAAAQAAAEUAAAEGAAAAHQAAAAEFAAABCAAAAQcAAAAeAAAAAQUBAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAEAAAEJAAAAHgAAAAEFAQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQACAAABCQAAAB8BAAABBQD#AAAAAAACAAAARQAAAQsAAAEKAAAAHQAAAAEFAAABBgAAAQcAAAAeAAAAAQUB#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAIAAAENAAAAEwEAAAEFAP8AAAAQAAABAAAAAgAAAPMAAAEOAAAAFgAAAAEFAf8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAADzAAAARQAAACAAAAABBQAAARAAAAARAQAAAQUA#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAIAAAAAEUAAAERAAAAIgD#####Af##AAAAAAEAAAAFAAAAUAAAAPQAAABfAAAAQQAAAFAAAAAjAP####8A##8AAAAAAAAFAAABEwAAACIA#####wH##wAAAAABAAAABQAAAPUAAABJAAAAPwAAAGAAAAD1AAAAIwD#####AP##AAAAAAAABQAAARUAAAADAP####8ABGNhczMAGihzdXAmYW5lZ3xpbmYmYXBvcykmcmFjcG9zAAAABQoAAAAFCwAAAAUKAAAABgAAABYAAAAGAAAAIwAAAAUKAAAABgAAAB4AAAAGAAAAIgAAAAYAAAAgAAAAFQD#####AAAALQAAAAUDAAAAAT#wAAAAAAAAAAAABQIAAAAGAAABFwAAAAYAAAABAAAAEQD#####AQB#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABNAAABGAAAABEA#####wEAfwAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAUgAAARgAAAARAP####8BAH8AABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFwAAAEYAAAAEQD#####AQB#AAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABdAAABGAAAABoA#####wARU2VnbWVudFNlbWlPdXZlcnQAAAAKAAAAAwAAAAMAAAADAAABGQAAARoAAAATAAAAAR0BAAAAABAAAAEAAAABAAABGQAAARoAAAAbAAAAAR0BAAAAAAAAAQAAARoAAAAGAAAAAwEAAAAcAAAAAR0BAAAAABAAAAEAAAABAAABGgAAAR4AAAAdAAAAAR0AAAEgAAABHwAAAB4AAAABHQEAAAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAQAAASEAAAAeAAAAAR0BAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAIAAAEhAAAAHwEAAAEdAP8AAAAAAAIAAAEaAAABIwAAASIAAAAdAAAAAR0AAAEeAAABHwAAAB4AAAABHQH#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAgAAASUAAAATAQAAAR0A#wAAABAAAAEAAAACAAABGQAAASYAAAAWAAAAAR0B#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAARkAAAEaAAAAIAAAAAEdAAABKAAAABEBAAABHQD#AAAAEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAgAAAABGgAAASkAAAAiAP####8B##8AAAAAAQAAAAUAAAEbAAABHAAAAGAAAABfAAABGwAAACMA#####wD##wAAAAAAAAUAAAErAAAAAwD#####AARjYXM0ABooc3VwJmFuZWd8aW5mJmFwb3MpJnJhY25lZwAAAAUKAAAABQsAAAAFCgAAAAYAAAAWAAAABgAAACMAAAAFCgAAAAYAAAAeAAAABgAAACIAAAAGAAAAIQAAABUA#####wAAAC0AAAAFAwAAAAE#8AAAAAAAAAAAAAUCAAAABgAAAS0AAAAGAAAAAQAAABEA#####wF#AH8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAATQAAAS4AAAARAP####8BfwB#ABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAAAAFIAAAEuAAAAEQD#####AX8AfwAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAABcAAABLgAAABEA#####wF#AH8AEAAAAAAAAAAAAAAAQAgAAAAAAAAAAAUAAAAAXQAAAS4AAAAaAP####8AEVNlZ21lbnRTZW1pT3V2ZXJ0AAAACgAAAAMAAAADAAAAAwAAATAAAAEvAAAAEwAAAAEzAQAAAAAQAAABAAAAAQAAATAAAAEvAAAAGwAAAAEzAQAAAAAAAAEAAAEvAAAABgAAAAMBAAAAHAAAAAEzAQAAAAAQAAABAAAAAQAAAS8AAAE0AAAAHQAAAAEzAAABNgAAATUAAAAeAAAAATMBAAAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAEAAAE3AAAAHgAAAAEzAQAAAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQACAAABNwAAAB8BAAABMwD#AAAAAAACAAABLwAAATkAAAE4AAAAHQAAAAEzAAABNAAAATUAAAAeAAAAATMB#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAFAAIAAAE7AAAAEwEAAAEzAP8AAAAQAAABAAAAAgAAATAAAAE8AAAAFgAAAAEzAf8AAAAQAAAAAAAAAAAAAABACAAAAAAAAAAABQAAAAEwAAABLwAAACAAAAABMwAAAT4AAAARAQAAATMA#wAAABAAAAAAAAAAAAAAAEAIAAAAAAAAAAAIAAAAAS8AAAE#AAAAIgD#####Af##AAAAAAEAAAAFAAABMQAAATIAAABgAAAAXwAAATEAAAAjAP####8A##8AAAAAAAAFAAABQf####8AAAABAB9DTWFjcm9BZmZlY3RhdGlvblZhbGV1clZhcmlhYmxlAP####8BAAD#AQAA#####xBAgzgAAAAAAEB1rXCj1wo+AgH2+v4AAAAAAAAAAAAAAAEAAAAAAAAAAAAIc29sdXRpb24AAAAAAAE#8AAAAAAAAAAAAAEAAAAXAP####8BAAD#AQAIc29sdXRpb27#####EEBzkAAAAAAAQHc9cKPXCj4AAfb6#gAAAAAAAAAAAAAAAQAAAAAAAAAABI5cYmVnaW57YXJyYXl9e2x9Clx0ZXh0e0EgcsOpc291ZHJlIDogJFxGb3JTaW1we2Z9XElme3N1cH17XGdlfXtcbGV9MCR9ClxcIFx0ZXh0eyR1KHgpPVxGb3JTaW1we3V9JCBlc3QgZGUgbGEgZm9ybWUgJGF4K2IkIGF2ZWMgJGE9XFZhbHthfSQgZXQgJGI9XFZhbHtifSQufQpcXCBcdGV4dHskdSh4KT0wIFxMZWZ0cmlnaHRhcnJvdyBcRm9yU2ltcHt1fT0wIFxMZWZ0cmlnaHRhcnJvdyB4PVxGb3JTaW1we3gwfSQufQpcXCBcdGV4dHtRdWFuZCAkeCQgZXN0IHBsdXMgZ3JhbmQgcXVlICRcRm9yU2ltcHt4MH0kICjDoCBkcm9pdGUgZGUgJFxGb3JTaW1we3gwfSQgc3VyIGxlIHRhYmxlYXUpLCAkdSh4KSQgYSBsZSBzaWduZSBkZSAkYT1cVmFse2F9JCBkb25jIGVzdCBpY2kgXElme2Fwb3N9e3Bvc2l0aWZ9e27DqWdhdGlmfS59ClxcIFx0ZXh0e0xlIHF1b3RpZW50ICRcRm9yU2ltcHtmfSQgcydhbm51bGUgcG91ciAkeD0wJCBldCBuJ2V4aXN0ZSBwYXMgcG91ciAkeD1cRm9yU2ltcHt4MH0kLCB2YWxldXIgcG91ciBsYXF1ZWxsZSBzb24gZMOpbm9taW5hdGV1ciBzJ2FubnVsZS59ClxcIFx0ZXh0eyRcRm9yU2ltcHt4MH0kIG4nZXN0IHBhcyBzb2x1dGlvbiBjYXIgbGUgcXVvdGllbnQgbidlc3QgcGFzIGTDqWZpbmkgcG91ciBjZXR0ZSB2YWxldXIgZXQgJDAkIGVzdCBzb2x1dGlvbiBjYXIgbGUgcXVvdGllbnQgZXhpc3RlIGV0IGVzdCBudWwgcG91ciBjZXR0ZSB2YWxldXIgZXQgbCdpbsOpZ2FsaXTDqSBlc3QgbGFyZ2UufQpcXCBcdGV4dHtPbiByZXDDqHJlIGRhbnMgbGEgZGVybmnDqHJlIGxpZ25lIGR1IHRhYmxlYXUgbGUgc2lnbmUgY2hlcmNoZSAoaWNpIGxlIHNpZ25lIFxJZntzdXB9eyt9ey19KSBldCBvbiBsaXQgZGFucyBsYSBwcmVtacOocmUgbGlnbmUgbCdlbnNlbWJsZSBkZXMgc29sdXRpb25zIChlbiByb3VnZSkufQpcXCBcdGV4dHtMJ2Vuc2VtYmxlIGRlcyBzb2x1dGlvbnMgZXN0IGRvbmN9ClxcIFx0ZXh0eyRTPQpcSWZ7Y2FzMX0KewpdLVxpbmZ0eTswXSBcY3VwIF1cRm9yU2ltcHt4MH07K1xpbmZ0eVsKfQp7ClxJZntjYXMyfQp7Cl0tXGluZnR5O1xGb3JTaW1we3gwfVsgXGN1cCBbMDsrXGluZnR5Wwp9CnsKXElme2NhczN9CnsKWzA7XEZvclNpbXB7eDB9Wwp9CnsKXVxGb3JTaW1we3gwfTswXQp9Cn0KfQokfQpcZW5ke2FycmF5ff###############w==
Sinon :
Utilisez l'icône ![]() pour créer une nouvelle figure sans repère et sans longueur unité.
pour créer une nouvelle figure sans repère et sans longueur unité.
Téléchargez ci-dessous deux bibliothèques de macro constructions créées pour simplifier le travail. Décompressez les deux fichiers zip dans le dossier de votre choix.
macrosaidepourmultietapes.zip tableauxsignesurr.zip
Pour adapter la couleur de fond de la figure à Labomep utilisez l'icône ![]() et choisissez l'item Couleur de fond de la figure puis choisissez comme couleur #f6fafe.
et choisissez l'item Couleur de fond de la figure puis choisissez comme couleur #f6fafe.
Si vous voulez éviter l'étape de création des calculs et fonctions ci-dessous, vous pouvez utiliser le code Base 64 ci-dessous en utilisant l'icône ![]() et en choisissant l'item Figure par code Base 64.
et en choisissant l'item Figure par code Base 64.
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcvb6#gEA#wEAAAAAAAAAAAUeAAACygAAAQEAAAAAAAAAAQAAACL#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AARwcm92AAExAAAAAT#wAAAAAAAAAAAAAgD#####AAVuYnZhcgABNQAAAAFAFAAAAAAAAAAAAAIA#####wAGbmJjYXMxAAE4AAAAAUAgAAAAAAAAAAAAAgD#####AAZuYmNhczIAATIAAAABQAAAAAAAAAAAAAACAP####8ABm5iY2FzMwABOAAAAAFAIAAAAAAAAAAAAAIA#####wAGbmJjYXM0AAEyAAAAAUAAAAAAAAAAAAAAAgD#####AAZuYmNhczUAATIAAAABQAAAAAAAAAAAAAACAP####8AAnIxABNpbnQocmFuZCgwKSpuYmNhczEp#####wAAAAIACUNGb25jdGlvbgL#####AAAAAQAKQ09wZXJhdGlvbgIAAAADEQAAAAEAAAAAAAAAAD#rBCChS0nK#####wAAAAEAD0NSZXN1bHRhdFZhbGV1cgAAAAMAAAACAP####8AAnIyABNpbnQocmFuZCgwKSpuYmNhczIpAAAAAwIAAAAEAgAAAAMRAAAAAQAAAAAAAAAAP+BxwGgbPjYAAAAFAAAABAAAAAIA#####wACcjMAE2ludChyYW5kKDApKm5iY2FzMykAAAADAgAAAAQCAAAAAxEAAAABAAAAAAAAAAA#7siza3qsOAAAAAUAAAAFAAAAAgD#####AAJyNAATaW50KHJhbmQoMCkqbmJjYXM0KQAAAAMCAAAABAIAAAADEQAAAAEAAAAAAAAAAD#qiYUoYeLgAAAABQAAAAYAAAACAP####8AAnI1ABNpbnQocmFuZCgwKSpuYmNhczUpAAAAAwIAAAAEAgAAAAMRAAAAAQAAAAAAAAAAP+ZTMuQkDQIAAAAFAAAABwAAAAIA#####wACYTEABHIxKzIAAAAEAAAAAAUAAAAIAAAAAUAAAAAAAAAAAAAAAgD#####AAJiMQAEcjMrMQAAAAQAAAAABQAAAAoAAAABP#AAAAAAAAAAAAACAP####8ABXNpZ25hAAcoLTEpXnIy#####wAAAAEACkNQdWlzc2FuY2X#####AAAAAQAMQ01vaW5zVW5haXJlAAAAAT#wAAAAAAAAAAAABQAAAAkAAAACAP####8ABXNpZ25iAAcoLTEpXnI0AAAABgAAAAcAAAABP#AAAAAAAAAAAAAFAAAACwAAAAIA#####wADc3VwAARyNT0wAAAABAgAAAAFAAAADAAAAAEAAAAAAAAAAAAAAAIA#####wABYQAIc2lnbmEqYTEAAAAEAgAAAAUAAAAPAAAABQAAAA0AAAACAP####8AAWIACHNpZ25iKmIxAAAABAIAAAAFAAAAEAAAAAUAAAAOAAAAAgD#####AAhhYnNhZGlmMQAJYWJzKGEpPD4xAAAABAkAAAADAAAAAAUAAAASAAAAAT#wAAAAAAAAAAAAAgD#####AAFnABNwZ2NkKGFicyhhKSxhYnMoYikp#####wAAAAEADUNGb25jdGlvbjJWYXICAAAAAwAAAAAFAAAAEgAAAAMAAAAABQAAABMAAAACAP####8ABWdkaWYxAARnPD4xAAAABAkAAAAFAAAAFQAAAAE#8AAAAAAAAAAAAAIA#####wACYScAA2EvZwAAAAQDAAAABQAAABIAAAAFAAAAFQAAAAIA#####wACYicAA2IvZwAAAAQDAAAABQAAABMAAAAFAAAAFQAAAAIA#####wADaW5mAAUxLXN1cAAAAAQBAAAAAT#wAAAAAAAAAAAABQAAABEAAAACAP####8AAngwAAYtYicvYScAAAAHAAAABAMAAAAFAAAAGAAAAAUAAAAXAAAAAgD#####AAZyYWNwb3MABHgwPjAAAAAEBQAAAAUAAAAaAAAAAQAAAAAAAAAAAAAAAgD#####AAZyYWNuZWcACDEtcmFjcG9zAAAABAEAAAABP#AAAAAAAAAAAAAFAAAAGwAAAAIA#####wAEYXBvcwADYT4wAAAABAUAAAAFAAAAEgAAAAEAAAAAAAAAAAAAAAIA#####wAEYW5lZwAGMS1hcG9zAAAABAEAAAABP#AAAAAAAAAAAAAFAAAAHQAAAAIA#####wAEemVybwABMAAAAAEAAAAAAAAAAP####8AAAABAAVDRm9uYwD#####AAF1AAVhKngrYgAAAAQAAAAABAIAAAAFAAAAEv####8AAAACABFDVmFyaWFibGVGb3JtZWxsZQAAAAAAAAAFAAAAEwABeAAAAAkA#####wABZgAJeC8oYSp4K2IpAAAABAMAAAAKAAAAAAAAAAQAAAAABAIAAAAFAAAAEgAAAAoAAAAAAAAABQAAABMAAXj###############8=
Notre exercice a besoin de 5 calculs aléatoires nommés nbcas1, nbcas2, …, nbcas5 et 5 calculs aléatoires nommés r1, r2, …, r5.
Par exemple, nbcas1, aura comme valeur 8 et ainsi j3p affectera lors des répétitions successives de l'exercice des valeurs comprises entre 0 et 7 au calcul nommé r1. Les formules entrées ci-dessous dans r1, r2, …, r5 ne servent qu'à simuler les formules qui seront affectés à ces calculs par LaboMep.
Dans la barre supérieure d'outils, utilisez l'icône ![]() qui fait apparaître des icônes supplémentaires puis utilisez l'icône
qui fait apparaître des icônes supplémentaires puis utilisez l'icône ![]() (gestion des constructions) et cliquez sur l'item Incorporer une construction depuis un fichier.
(gestion des constructions) et cliquez sur l'item Incorporer une construction depuis un fichier.
Allez dans le dossier dans lequel vous avez décompressé les deux fichiers zip ci-dessus et sélectionnez dans la liste le fichier InitRand5Val.mgc puis cliquez sur le bouton Ouvrir. Cette macro construction fait maintenant partie de votre figure.
Pour être utilisée, cette macro construction nécessite comme objet source un calcul dont la valeur importe peu.
Utilisez l'icône ![]() pour créer un calcul nommé prov avec comme formule 0.
pour créer un calcul nommé prov avec comme formule 0.
Utilisez de nouveau l'icône ![]() et cliquez sur l'item Implémenter une construction de la figure.
et cliquez sur l'item Implémenter une construction de la figure.
La seule macro de notre figure est déjà sélectionnée dans la liste proposée. Cliquez sur le bouton Implémenter.
Une nouvelle boîte de dialogue s'ouvre vous demandant de choisir quel objet utiliser comme objet source de cette macro construction.
Dans la liste, sélectionnez le calcul prov comme ci-dessous.
Validez par OK.
Cette macro construction a créé pour vous certains calculs mais pour les modifier il vous faut utiliser l'icône ![]() puis cliquez sur l'item Fusionner les constructions de la figure.
puis cliquez sur l'item Fusionner les constructions de la figure.
Utilisons maintenant l'outil ![]() permettant de modifier les objets de la figure qui sont de type calcul.
permettant de modifier les objets de la figure qui sont de type calcul.
Pour chacun des calculs ci-dessous, utilisez le bouton Modifier pour le modifier (un double clic sur le calcul permet aussi de le modifier).
Utilisez l'icône ![]() pour créer les calculs réels suivants :
pour créer les calculs réels suivants :
| Nom du calcul | Ancienne formule | Nouvelle formule | Commentaire |
|---|---|---|---|
| nbvar | 5+0*prov | 5 | Nombre de variables servant à choisir les valeurs aléatoires |
| nbcas1 | prov | 8 | Nombre de valeurs possibles pour la valeur absolue de a |
| nbcas2 | prov | 2 | Nombre de valeurs possibles pour le signe de a |
| nbcas3 | prov | 8 | Nombre de valeurs possibles pour la valeur absolue de b |
| nbcas4 | prov | 2 | Nombre de valeurs possibles pour le signe de b |
| nbcas5 | prov | 2 | Nombre de valeurs possibles le type d'inéquation (≤ ou ≥) |
La macro construction a aussi créé pour vous les calculs suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| r1 | int(rand(0)*nbcas1) | Sert à simuler les valeurs qui seront affectés à r1 lors des répétitions |
| r2 | int(rand(0)*nbcas2) | Sert à simuler les valeurs qui seront affectés à r2 lors des répétitions |
| r3 | int(rand(0)*nbcas3) | Sert à simuler les valeurs qui seront affectés à r3 lors des répétitions |
| r4 | int(rand(0)*nbcas4) | Sert à simuler les valeurs qui seront affectés à r4 lors des répétitions |
| r5 | int(rand(0)*nbcas5) | Sert à simuler les valeurs qui seront affectés à r5 lors des répétitions |
Utilisez l'icône ![]() pour créer les calculs suivants :
pour créer les calculs suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| a1 | r1+2 | représentera la valeur absolue de a qui pourra aller de 2 à 9 |
| signa | (-1)^r2 | Vaurdra 1 si a est positif et (-1) si a est négatif |
| b1 | r3+1 | représentera la valeur absolue de a qui pourra aller de 1 à 8 |
| signb | (-1)^r4 | Vaurdra 1 si b est positif et (-1) si b est négatif |
| sup | r5=0 | Vaudra 1 pour une inéquation du type ≥ et 0 pour une inéquation du type ≤ |
| a | signa*a1 | Valeur de a (pour l'étude du signe de ax+b) |
| b | signb*b1 | Valeur de b (pour l'étude du signe de ax+b) |
| absadif1 | abs(a)<>1 | Vaudra 1 si a = 1 ou a = -1 et 0 sinon |
| g | pgcd(abs(a),abs(b)) | Contiendra le PGCD des valeurs absolues de a et b |
| gdif1 | g<>1 | Vaudra 1 si a et b sont premiers entre eux et 0 sinon |
| a' | a/g | Numérateur de la fraction irréductible représentant le quotient a/b |
| b' | b/g | Dénominateur de la fraction irréductible représentant le quotient a/b |
| inf | 1-sup | Vaudra 0 pour une inéquation du type ≥ et 1 pour une inéquation du type ≤ |
| x0 | -b'/a' | Fraction réduite représentant la valeur qui annule ax+b |
| racpos | x0>0 | Vaudra 1 si x0 est positif et 0 sinon |
| racneg | 1-racpos | Vaudra 1 si x0 est négatiget 0 sinon |
| apos | a>0 | Vaudra 1 si a est positif et 0 sinon |
| aneg | 1 - apos | Vaudra 1 si a est négatif et 0 sinon |
| zero | 0 | Représentera le nombre 0 (utilisé pour des tests d'équivalence) |
Maintenant utilisez l'icône ![]() pour créer les deux fonctions de la variable réelle x suivante :
pour créer les deux fonctions de la variable réelle x suivante :
| Nom de la fonction | Formule |
|---|---|
| u | u(x)=ax+b |
| f | f(x)=x/(a*x+b) |
Si vous avez utilisé le code Base 64 précédent pour sauter la création des calculs, vous devez reprendre le tutoriel ici.
Nous allons maintenant utiliser un macro construction qui va créer pour nous certains objets nécessaires pour la création d'un exercice en deux étapes.
Cliquez sur l'icône ![]() (gestion des constructions). et choisissez l'item Incorporer une construction depuis un fichier.
(gestion des constructions). et choisissez l'item Incorporer une construction depuis un fichier.
Allez dans le dossier dans lequel vous avez décompressé le fichier macrosPourMultiEtapes.zip.
Choisissez le fichier Preparation2Etapes.mgc et validez.
Cliquez de nouveau sur l'icône ![]() et choisissez l'item Implémenter une construction de la figure.
et choisissez l'item Implémenter une construction de la figure.
L'implémentation de cette macro nécessite aussi un calcul comme objet source 1. Sélectionnez le calcul prov dans la liste des objets proposés puis validez. La macro est implémentée.
Lorsqu'on implémente une construction, les objets finaux qu'elle génère ne sont pas modifiables (à part leur aspect).
Ici nous aurons besoin de les modifier.
Pour pouvoir modifier les objets que la macro construction a créés, utilisez l'icône ![]() et cliquez sur l'item Fusionner les constructions de la figure.
et cliquez sur l'item Fusionner les constructions de la figure.
Vous voyez apparaître sur la figure deux macros et des affichages LaTeX. En utilisant l'outil ![]() puis en cliquant sur la macro Etape1 ou Etape2 vous changez la valeur de la variable etape créée par la macro, ce qui fait apparaître ou disparaître les objets utiles pour chacune des ses étapes.
puis en cliquant sur la macro Etape1 ou Etape2 vous changez la valeur de la variable etape créée par la macro, ce qui fait apparaître ou disparaître les objets utiles pour chacune des ses étapes.
En utilisant dans la barre supérieure l'outil ![]() vous vrrez que la construction a aussi créé un calcul nomme nbEtapes avec comme formule 2+0*prov. Vous pouvez remplacer la formule par 2 (il fallait que ce calcul dépende de prov pour que ce soit un objet final de construction). La présence de ce calcul est indispensable pour que LaboMep sache que cet exercice se déroule en deux étapes.
vous vrrez que la construction a aussi créé un calcul nomme nbEtapes avec comme formule 2+0*prov. Vous pouvez remplacer la formule par 2 (il fallait que ce calcul dépende de prov pour que ce soit un objet final de construction). La présence de ce calcul est indispensable pour que LaboMep sache que cet exercice se déroule en deux étapes.
Il est maintenant temps de créer notre tableau de signes.
Utilisez d'abord l'icône ![]() pour créer un point libre en haut et à gauche de la figure. Ce point libre définira la bord haut et gauche de notre tableau de signes.
pour créer un point libre en haut et à gauche de la figure. Ce point libre définira la bord haut et gauche de notre tableau de signes.
Cliquez ensuite sur l'icône ![]() (gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
(gestion des constructions) et choisissez l'item Incorporer une construction depuis un fichier.
Allez dans le dossier où vous avez décompressé le fichier tableauxsignesurr.zip contenant la construction et cliquez sur le fichier nommé TableauSignes2Val3LignesEtape1.mgc.
Cette construction fait maintenant partie de votre figure et peut être utilisée.
Utilisez à nouveau l'icône ![]() et choisissez l'item Implémenter une construction de la figure.
et choisissez l'item Implémenter une construction de la figure.
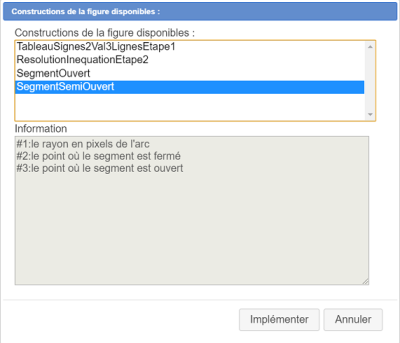
Une boîte de dialogue s'ouvre comme ci-dessous vous présentant les constructions de la figure comme ci-dessous. Sélectionnez dans la liste la macro nommée TableauSignes2Val3LignesEtape1 .
Cliquez sur le bouton implémenter.
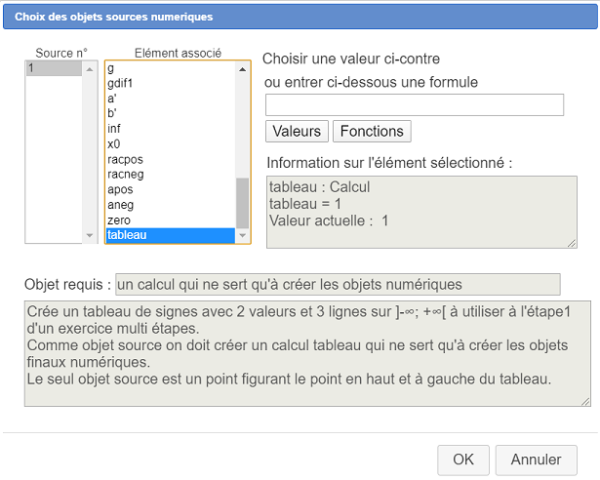
Quand on implémente une construction il faut toujours choisir les objets sources numériques en premier.
Une boîte de dialogue s'ouvre donc pour choisir le seul objet source.
Comme ci-dessous, affectez à l'élément source n°1 le calcul que nous avons nommé prov.
Puis validez par OK.
En haut et à droite de la fenêtre MathGraph32 on vous demande de cliquer sur le point extérieur gauche du tableau. Cliquez sur le point libre que vous avez créé précédemment.
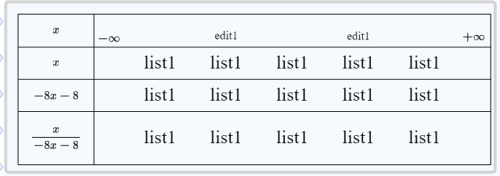
Votre figure ressemble maintenant à ceci :
Utilisez l'icône ![]() (gestion des constructions) et choisissez l'item Fusionner les constructions de la figure puis validez. Les objets créés par la construction sont maintenant modifiables.
(gestion des constructions) et choisissez l'item Fusionner les constructions de la figure puis validez. Les objets créés par la construction sont maintenant modifiables.
Vous pouvez maintenant utiliser l'outil ![]() (outil protocole de la barre supérieure) pour voir tous les objets rajoutés par la construction. Il y a des objets de nature graphique et des objets de nature numérique.
(outil protocole de la barre supérieure) pour voir tous les objets rajoutés par la construction. Il y a des objets de nature graphique et des objets de nature numérique.
En particulier vous trouverez un calcul nommé etapeInterne1 dont la formule est 1+0*prov. Il était nécessaire que ce calcul dépende de tableau pour qu'il soit généré par la construction mais vous pouvez maintenant remplacer sa formule par 1 (ou le garder tel quel). La présence de ce calcul et sa valeur 1 servent à indiquer à LaboMep que la validation de cette première étape se fera via des éditeurs internes à la figure MathGraph32.
Déplacez-vous dans la liste de gauche pour sélectionner l'affichage LaTeX lat3 et cliquez sur l'icône ![]() pour le modifier.
pour le modifier.
Son code LaTeX actuel est expr1. Remplacez ce code par x.
De même sélectionnez l'affichage LaTeX lat4 et remplacez son code LaTeX par x.
Puis sélectionnez la LaTeX lat5 et remplacez le code LaTeX par ce qui suit (vous pouvez utiliser le bouton Insertion de formule :
\ForSimp{u}
Nous afficherons donc ici la formmule (simplifiée si nécessaire) de la fonction u c'est-à-dire ax+b avec les valeurs de a et b remplacées.
De même sélectionnez l'affichage LaTeX lat6 et remplacez son code LaTeX par :
\ForSimp{f}
Nous afficherons donc ici la formule de la fonction f c'est-à-dire x/(ax+b) avec les valeurs de a et b remplacées.
A noter que vous pouvez modifier les dimensions du tableau en quittant la boîte de dialogue, en utilisant l'outil de capture ![]() et en capturant les points sur le segment de gauche du tableau ou les points sur le segment du haut. Cela vous permet d'adapter les dimensions du tableau à ce qu'il contient.
et en capturant les points sur le segment de gauche du tableau ou les points sur le segment du haut. Cela vous permet d'adapter les dimensions du tableau à ce qu'il contient.
Revenons à notre boîte de dialogue de protocole.
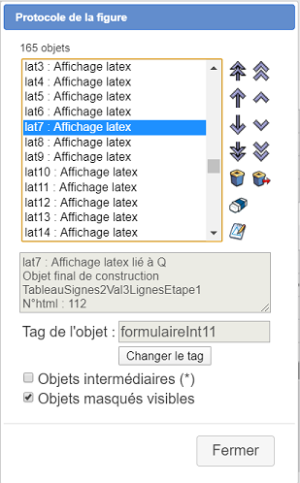
Utilisez la touche du clavier ↓ (ou l'icône correspondante) pour vous déplacer dans les objets créés jusqu'à l'objet lat7 comme ci-dessous. C'est un affichage LaTeX correspondant au premier edit1 sur la figure.
Vous pouvez voir que cet affichage LaTeX possède un tag : formulaireInt11.
Le premier 1 correspondant l 'étape (ici l'étape 1) et le second 1 indique que c'est le premier formulaire de la figure à l'étape 1.
Lorsque Labomep communiquera avec cette figure il saura d'après son tag qu'il faut remplacer cet affichage LaTeX par un éditeur de formule mathquill et que c'est le premier éditeur de formule de la figure.
Pour voir comment a été conçu cet affichage LaTeX cliquez sur l'icône ![]() (toujours dans la boîte de dialogue de protocole).
(toujours dans la boîte de dialogue de protocole).
Vous voyez que le code LaTeX est : \text{edit1}
Cela signifie que cet affichage LaTeX correspondra à un éditeur mathquill contenant un seul éditeur de formule (ce qui sera toujours le cas pour un tableau de signes ou de variations).
D'autre part la taille de cet affichage LaTeX est de 16. Cette taille sera celle des caractères de l'éditeur.
Un autre point important : en bas et à gauche de la boîte de dialogue LaTeX vous pouvez voir que l'affichage (qui est lié au point provisoirement nommé Q) est centré horizontalement et aligne verticalement au-dessus de point. Il en sera de même pour l'éditeur mathquill.
Refermez la boîte de dialogue associée à cet affichage LaTeX et descendez d'un cran dans la liste des objets créés.
L'objet suivant lat8 est un autre affichage LaTeX. Son tag est solInt11.
Ce tag indiquera à LaboMep qu'il contient la formule LaTeX à afficher lors de la correction de la première étape.
Pour le modifier, cliquez sur l'icône ![]() (toujours dans la boîte de dialogue de protocole) ou double cliquez sur lat8 dans la liste de gauche.
(toujours dans la boîte de dialogue de protocole) ou double cliquez sur lat8 dans la liste de gauche.
Le code LaTeX provisoire est 1. Remplacez ce code LaTeX par le code suivant :
\If{racpos}{0}{\ForSimp{x0}}
Nous utilisons ici un affichage LaTeX conditionnel spécifique à MathGraph32. Ainsi, si x0 est positif (quand le calcul racpos vaut1 donc) on affichera 0 et sinon on affichera la formule de x0 (fraction réduite -b'/a').
Validez la boîte de dialogue LaTeX et, dans la liste de gauche du protocole, descendez jusqu'à l'affichage LaTeX lat9.
Vous voyez que son tag est formulaireInt12. Il sera donc remplacé par le deuxième éditeur mathquill (le 1 correspondant à l'étape).
Au-dessous passons à l'affichage LaTeX lat10.
Son tag est solInt121. Il contiendra donc la correction pour le premier éditeur de formule de l'éditeur mathquill numéro 2 à l'étape 1.
Pour le modifier, cliquez sur l'icône ![]() (toujours dans la boîte de dialogue de protocole) ou double cliquez sur lat10 dans la liste de gauche.
(toujours dans la boîte de dialogue de protocole) ou double cliquez sur lat10 dans la liste de gauche.
Le code LaTeX provisoire est 2. Remplacez-le par le code LaTeX suivant :
\If{racpos}{\ForSimp{x0}}{0}
Nous verrons plus tard comment vérifier la réponse de l'élève dans ces deux éditeurs.
Validez la boîte de dialogue LaTeX et passez dans la liste de gauche à l'affichage LaTeX suivant : lat11.
Son tag est formulaireInt13. Ce sera donc le troisième éditeur de formule du tableau.
Utilisez l'icône ![]() pour voir quel est son code LaTeX. C'est le code suivant :
pour voir quel est son code LaTeX. C'est le code suivant :
\text{list1}
Cet éditeur de formule sera donc constitué d'une unique liste déroulante.
Refermez la boîte de dialogue LaTeX.
Dans la liste de gauche, activez l'affichage LaTeX lat12.
Son code LaTeX est le suivant :
\begin{array}{l}
\text{+}
\\ \text{-}
\\ \text{0}
\end{array}
Chacune des \text de ce code contient un des items d la future liste déroulante. La liste déroulante proposera donc 3 items : +, - et 0.
Inutile de le modifier.
Tous les affichages LaTeX suivant sont du même type et seront remplacés par des listes déroulantes.
L'avant dernier d'entre-eux est lat39 et son tag est formulaireInt117 : c'est le 17 ième éditeur de à l'étape 1.
Le dernier d'entre-eux est lat40 et son tag est listInt1171 : On est à l'étape 1, dans 17 ième formulaire et il s'agit des items proposés par la première (et unique) liste de cet éditeur.
Intéressons nous maintenant aux objets numériques rajoutés par la construction, objets qui serviront à valider les réponses de l'élève.
En restant toujours dans la boîte de dialogue de protocole, descendez dans la liste jusqu'aux calculs nommés repInt111 et repInt121.
Ces calculs n'ont pas à être modifiés.
Par exemple pour le calcul repInt121 il est destiné à contenir la réponse de l'élève à l'étape 1, au deuxième éditeur et, à l'intérieur de cet éditeur au premier éditeur de formule mathquill (le nom finira toujours par 1 ici).
Le fait que ces calculs contiennent comme formule prov a permis de les construire comme objets finaux de la constructions (ils devaient dépendre d'au moins un objet source, ici notre calcul prov).
Au fur et à mesure que vous modifierez les formules, vous pourrez retirer les références à prov. On peut par exemple ici entrer comme formule 0 pour ces deux calculs, mais ce n'est pas indispensable pour le bon fonctionnement de notre exercice.
Descendez dans la liste de gauche jusqu'au calcul nommé resoluInt111.
Ce calcul doit correspondre à la validation de la réponse de l'élève dans l'éditeur mathquill du premier formulaire. Il doit valoir 1 si la réponse est acceptée comme bonne et 0 sinon.
Pour le moment sa formule est tableau et nous allons devoir le modifier.
Mais auparavant nous devons créer quatre tests d'équivalence.
Pour cela quittez la boîte de dialogue de protocole.
Déroulez la barre d'outils des calculs et, à sa droite, cliquez sur l'icône ![]() qui fait apparaître un choix d'outils supplémentaires.
qui fait apparaître un choix d'outils supplémentaires.
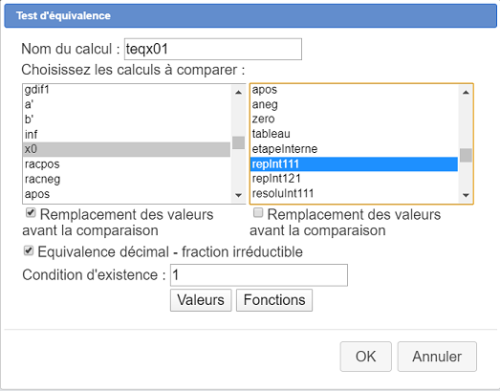
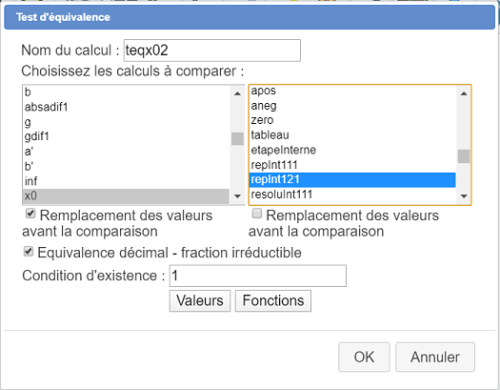
Choisissez l'item Test d'équivalence et validez.
Une boîte de dialogue s'ouvre. Remplissez là comme ci-dessous.
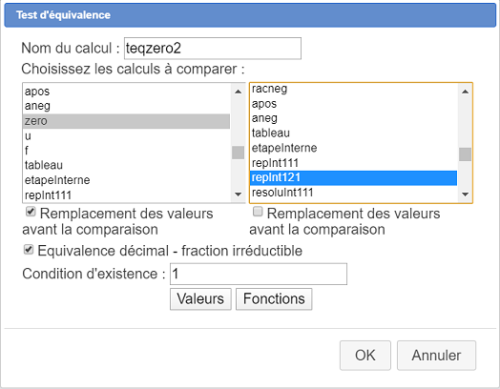
Procédez de même pour créer un autre test d'équivalence comme ci-dessous :
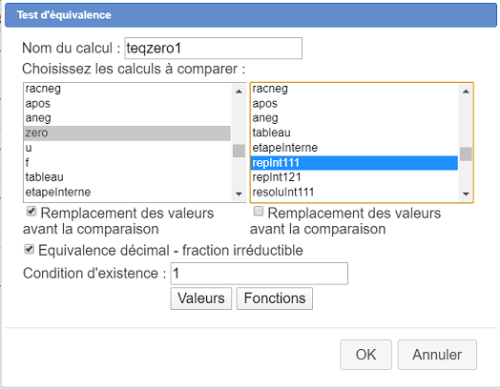
Créez deux autres tests d'équivalence comme ci-dessous (ils serviront pou valider la réponse pour le deuxième formulaire de la première ligne du tableau) :
Pour que les calculs nommés resoluInt111 et resoluInt121 puissent utiliser ces tests d'équivalence nous devons procéder à du reclassement d'objets. Nous allons reclasser vers lla fin les deux calculs resoluInt111 et resoluInt121.
Activez de nouveau l'outil protocole ![]() et sélectionnez dans la liste le calcul resoluInt111 (il est possible de taper au clavier les premières lettres du nom pour aller plus vite).
et sélectionnez dans la liste le calcul resoluInt111 (il est possible de taper au clavier les premières lettres du nom pour aller plus vite).
Cliquez ensuite à droite sur l'icône ![]() qui permet de reclasser un objet le plus loin possible dans la liste des objets créés.
qui permet de reclasser un objet le plus loin possible dans la liste des objets créés.
Dans la liste de gauche, sélectionnez maintenant le calcul resoluInt121 et, de la même façon, reclassez ce calcul vers la fin.
Maintenant sélectionnez dans la liste le calcul resoluInt111 et remplacez sa formule par :
si(racpos,teqzero1,teqx01)
En effet, si x0 est positif, l'élève doit avoir rentré comme réponse 0 et sinon la fraction irréductible dont la formule est dans x0.
De même sélectionnez dans la liste le calcul resoluInt121. Replacez sa formule par :
si(racpos,teqx02,teqzero2)
Il nous faut maintenant modifier les calculs servant à savoir quelle est la bonne réponse pour chacune des listes déroulantes du tableau.
Par exemple nous avons vu que le formulaire associé à la première liste du tableau était donné par l'affichage LaTeX de tag formulaire13 (c'est le troisième formulaire à l'étape 1). Nous avons aussi vu que l'affichage LaTeX donnant les 2 items de la liste déroulante associée avait pour tag listInt131. Le calcul indiquant quel est l'indice de la bonne réponse pour cette liste déroulante se nomme resListInt131 et a été créé par la construction. Nous devrons donc mettre dans ce calcul comme formule 2 qui correspond au deuxième item de la liste déroulante (le signe -).
Vous allez donc modifier les calculs suivants de la façon suivante :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| resListInt131 | 2 | Correspond au signe -, deuxième item de la liste déroulante associée. |
| resListInt141 | si(racpos,3,1) | Si x0 est positif, il faut un zéro (item n°3) et sinon une barre simple (item n°1) |
| resListInt151 | si(racpos,1,2) | si x0 est positif, il faut un signe - et sinon un signe + |
| resListInt161 | si(racpos,1,3) | si x0 est positif, il faut une barre simple et sinon un zéro |
| resListInt171 | 1 | Il faut un signe + dans cette case |
On passe à la ligne suivante du tableau qui demande le signe de ax+b.
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| resListInt181 | si(apos,2,1) | si a est positif, il faut un signe - et sinon un signe + |
| resListInt191 | si(racpos,1,3) | si x0 est positif, il faut une barre simple et sinon un zéro |
| resListInt1101 | si(racpos,si(apos,2,1),si(apos,1,2)) | |
| resList1111 | si(racpos,3,1) | |
| resList1121 | si(apos,1,2) |
Passons à la dernière ligne du tableau qui demande le signe du quotient x/(ax+b)
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| resList1131 | si(apos,1,2) | |
| resList1141 | si(racpos,3,2) | |
| resList1151 | si(apos,2,1) | |
| resList1161 | si(racpos,2,3) | |
| resList1171 | si(apos,1,2) |
Nous avons fini de préparer ce qui est nécessaire pour la première étape : remplir le tableau de signes.
Préparons des affichages LaTeX qui fourniront les consignes à donner aux élèves.
Déroulez la barre d'outils des affichages et activez l'icône ![]() (création d'un affichage LaTeX libre).
(création d'un affichage LaTeX libre).
Cliquez sur l'affichage LaTeX destiné à contenir la consigne à l'étape 1.
Une boîte de dialogue s'ouvre pour modifier le code LaTeX. Remplacez le code LaTeX par le code LaTeX suivant :
\begin{array}{l}
\text{Le but de cet exercice est de résoudre l'inéquation $\ForSimp{f}\If{sup}{\ge}{\le}0$.}
\\ \text{$\textcolor{maroon}{\text{Dans un premier temps on demande de remplir le tableau de signes suivant :}}$}
\\ \text{(Les valeurs de la première ligne doivent être simplifiées au maximum)}
\end{array}
Maintenant préparons la deuxième étape : activez l'outil ![]() (exécution de macro) et cliquez sur la macro Etape2.
(exécution de macro) et cliquez sur la macro Etape2.
Avant de modifier le code LaTeX donnant l'énoncé à l'étape 2, nous avons d'abord besoin de créer deux fonctions de la variable x que nous nommerons for1 et for2.
Pour cela utilisez l'icône ![]() de création de fonction réelle d'une variable réelle.
de création de fonction réelle d'une variable réelle.
| Nom de la fonction de la variable x | Formule |
|---|---|
| for1 | a*x=-b |
| for2 | x=-b/a |
Pour que l'affichage LaTeX fournissant la consigne à l'étape 2 ouisse utiliser ces deux fonctions, il doit être reclassé vers la fin des objets créés. Utilisez pour cela l'outil ![]() et cliquez sur l'affichage LaTeX destiné à contenir la consigne à l'étape 2.
et cliquez sur l'affichage LaTeX destiné à contenir la consigne à l'étape 2.
Activez de nouveau l'outil de modification d'objet graphique ![]() et cliquez sur cet affichage LaTeX. Remplacez son code par le code ci-dessous:
et cliquez sur cet affichage LaTeX. Remplacez son code par le code ci-dessous:
\begin{array}{l}
\text{$u(x)=\ForSimp{u}$ est de la forme $ax+b$ avec $a=\Val{a}$ et $b=\Val{b}$.}
\\ \text{$u(x)=0 \Leftrightarrow \ForSimp{u}=0 \If{absadif1}{\Leftrightarrow \ForSimp{for1} \If{gdif1}{\Leftrightarrow \ForSimp{for2}}{}}{} \Leftrightarrow x=\ForSimp{x0}$.}
\\ \text{Quand $x$ est "à droite" de $\ForSimp{x0}$, $u(x)$ a le signe de $a=\Val{a}$ donc est ici \If{apos}{positif}{négatif}.}
\\ \text{Le quotient $\ForSimp{f}$ s'annule pour $x=0$ et n'existe pas pour $x=\ForSimp{x0}$, valeur pour laquelle son dénominateur s'annule.}
\\ \text{$\textcolor{maroon}{\text{A l'aide du tableau de signes ci-dessous, on demande maintenant de donner}}$}
\\ \text{$\textcolor{maroon}{\text{l'ensemble des solutions }S\text{ de l'inéquation }\ForSimp{f}\If{sup}{\ge}{\le}0}$.}
\end{array}
Cet affichage fournit des indications sur ce qu'il fallait faire à l'étape 1 et donne la consigne de ce qu'il faut faire à l'étape 2.
A noter que si le calcul sup vaut 1 nous demanderons de résoudre l'inéquation x/(ax+b) ≥ 0 et que sinon nous demanderons de résoudre l'inéquation x/(ax+b) ≤ 0.
Maintenant cliquez sur l'affichage LaTeX destiné à contenir le formulaire à remplir à l'étape 2.
Remplacez son code LaTeX par le code suivant :
\text{$S$ = edit1}
A l'étape 2, il sera affiché S = suivi d'un éditeur de formule dans lequel l'élève devra entrer l'ensemble des solutions de l'inéquation.
Pour la vérification de la réponse de l'élève, nous allons nous aider d'une autre construction qui créera les éléments nécessaires, éléments que nous adapterons à cet exercice.
Cette construction était contenue dans la fichier zippé nommé aidepourmultietapes.zip.
Pour incorporer cette construction dans votre figure, utilisez l'icône ![]() et choisissez l'item incorporer une construction depuis un fichier.
et choisissez l'item incorporer une construction depuis un fichier.
Allez dans le dossier dans lequel vous avec décompressé les constructions, sélectionnez le fichier preparationInequationEtape2.mgc puis cliquez sur le bouton Ouvrir. La construction fait maintenant partie de votre figure et peut être utilisée.
Cette construction a juste besoin d'un objet source numérique. Nous utiliserons pour cela le calcul prov créé précédemment.
Pour implémenter cette construction dans la figure, utilisez à nouveau l'icône ![]() et choisissez l'item Implémenter une construction de la figure.
et choisissez l'item Implémenter une construction de la figure.
Une boîte de dialogue vous présente les constructions présentes dans la figure. Cette fois il faut sélectionner la construction nommée PreparationInequationEtape2 puis cliquer sur le bouton Implémenter.
Une boîte de dialogue vous demande alors de choisir les éléments sources numériques (un seul ici). Choisissez comme objet source numéro 1 le calcul prov comme ci-dessous et validez.
Les objets de type calcul qui ont été créés sont adaptés au cas où la bonne solution serait l'intervalle ]-∞;0]U]1;2] ce qui n'est bien sûr pas le cas ici et que nous allons devoir adapter.
Mais pour pouvoir les modifier vous devez de nouveau utiliser l'icône ![]() et activer l'item Fusionner les constructions de la figure.
et activer l'item Fusionner les constructions de la figure.
Ici nous aurons quatre solutions possibles. Nous allons donc créer quatre fonctions qui représenteront les quatre solutions attendues (le nom de ces calculs n'est pas imposé par le modèle).
Déroulez la barre des calculs et utilisez l'icône ![]() pour créer 4 fonctions de la variables réelle x nommés solution1, solution2, solution3 et solution4 4 avec comme formule provisoire 0.
pour créer 4 fonctions de la variables réelle x nommés solution1, solution2, solution3 et solution4 4 avec comme formule provisoire 0.
C'est le calcul nommé rep2 créé par la construction qui est censé recevoir la réponse de l'élève (sous forme d'une formule de fonction utilisant des booléens si nécessaire). Seulement sa présence est nécessaire. Le reste est géré par le modèle.
Déroulez la barre des calculs, cliquez à sa droite sur l'icône ![]() et choisissez l'item Test d'équivalence.
et choisissez l'item Test d'équivalence.
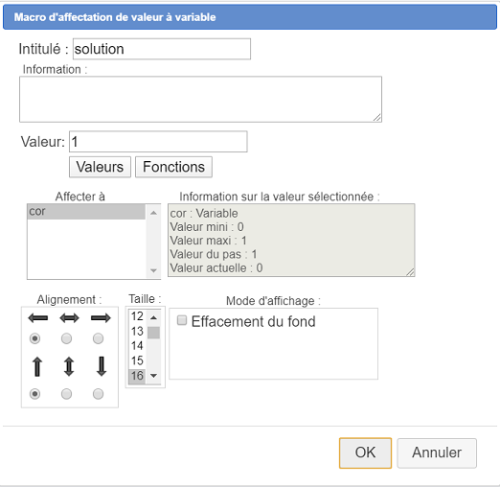
Remplissez la boîte de dialogue comme ci-dessous pour créer un test d'équivalence entre solution1 et rep2 nommé teq1 (avec remplacement des valeurs seulement pour solution1) :
Procédez de même pour créer un test d'équivalence teq2 entre solution2 et rep2, un test d'équivalence teq3 entre solution3 et rep2 et un test d'équivalence teq4 entre solution4 et rep2.
Sélectionnez dans la liste de gauche la fonction solution1 et utilisez l'icône ![]() pour reclasser cette fonction juste après le calcul etapeResIneq2 comme ici :
pour reclasser cette fonction juste après le calcul etapeResIneq2 comme ici :  .
.
Procédez de même pour reclasser solution2, solution3 et solution4 juste au-dessous de solution1, teq1, teq2, teq3 et teq4 juste au-dessous de rep2.
Maintenant, toujours dans la boîte de dialogue de protocole, vous allez modifier les calculs ou fonctions créés par la macro construction en utilisant l'icône ![]() ou en double-cliquant sur le nom du calcul ou de la fonction
ou en double-cliquant sur le nom du calcul ou de la fonction
| Nom du calcul ou de la fonction | Ancienne formule | Nouvelle formule | Commentaire | |
|---|---|---|---|---|
| etapeResIneq2 | 1+0*prov | 1 | L'utilisation du calcul prov n'est plus nécessaire une fois la construction implémentée | |
| solution1 | 0 | x⇐0|x>-b'/a' | Correspond au cas où l'ensemble des solutions est l'extérieur des racines et -b/a>0 | |
| solution2 | 0 | x<-b'/a'|x>=0 | Correspond au cas où l'ensemble des solutions est l'extérieur des racines et -b/a<0 | |
| solution3 | 0 | x>=0&x<-b'/a' | Correspond au cas où l'ensemble des solutions est l'intérieur des racines et -b/a>0 | |
| solution4 | 0 | x>-b'/a'&x⇐0 | Correspond au cas où l'ensemble des solutions est l'intérieur des racines et -b/a>0 | |
| fonctionTest | 0*prov | 0 | Sert à communiquer avec LaboMep | |
| repBornesFermees2 | 0*prov | 0 | Sert à communiquer avec j3P. Correspond à la réponse de l'élève avec des bornes d'intervalles toutes fermées. Pas utilisé ici car on ne donne pas d'indication en cas de faute de crochet | |
| sol21 | x<=0|x>1&x<=2+0*prov | 0 | Est implémenté à titre d'exemple. Ne sera pas utilisé ici | |
| sol22 | x<=0|x>=1&x<=2+0*prov | 0 | Est implémenté à titre d'exemple. Ne sera pas utilisé ici | |
| xTest | 0+0*prov | 0 | idem. Ce calcul sert lors des échanges entre LaboMep et la figure MathGraph32. | |
| eps | 0.000000000001+0*prov | 0.000000000001 | idem | |
| zeroBorne | abs(x)<eps | Cette formule ne doit pas être modifiée | ||
| estBorneFermee2 | zeroBorne(xTest-0) | zeroBorne(xTest-2) | zeroBorne(xTest-0) | Cette fonction doit renvoyer1 si xTest est proche d'une des bornes formées d'un des intervalles solutions. Ici la seule borne fermée est 0. |
| plusInfSolution2 | 0+0*prov | sup&apos|inf&aneg | doit valoir 1 quand l'ensemble des solutions est non borné à droite ce qui est vrai ici quand l'ensemble des solutions est l'extérieur des racines | |
| moinsInfSolution2 | 0+0*prov | sup&apos|inf&aneg | doit valoir 1 quand l'ensemble des solutions est non borné à gauche ce qui est vrai ici quand l'ensemble des solutions est l'extérieur des racines | |
| toutReelSol2 | 0+0*prov | 0 | 0 (pour faux) car il n'y a aucun cas ici où l'ensemble des solutions soit R | |
| vide2 | 0+0*prov | 0 | 0 (pour faux) car l'ensemble des solutions n'est jamais vide | |
| contientBorne2 | fonctionTest(0)|fonctionTest(1)|fonctionTest(2) | fonctionTest(0)|fonctionTest(x0) | Appeler fonctionTest pour chacune des bornes (fermée ou non) avec un ou logique | |
| rep2 | 0*prov | 0 | Contiendra la formule correspondant à la réponse entrée par l'élève | |
| repPourBornes2 | 0*prov | 0 | Servira à communiquer entre la figure et LaboMep | |
| nbSolIsolees2 | 0*prov | 0 | 0 (pour faux) car ici il n'y a pas de solution isolée | |
| estSolIsolee2 | 0*prov+zeroBorne(xTest-100) | 0 | 0 (pour faux) car par exemple l'ensemble des solutions n'est pas de la forme R - {1;2} auquel cas il y aurait deux solution isolées 1 et 2 | |
| estBorneIsolee2 | 0*prov+zeroBorne(xTest-50) | 0 | 0 (pour faux) car par exemple l'ensemble des solutions n'est pas de la forme [0;3[U ]3;4] auquel cas 3 serait une borne isolée | |
| repPourBornes2 | 0*prov | 0 | Servira à communiquer entre la figure et LaboMep | |
| solutionBornesFermees2 | x<=0|x>=1 | 0 | Nous n'utiliserons pas cette fonction car nous ne souhaitons pas donner d'indication si l'ensemble des solutions est faux à cause d'une erreur de crochet |
Le calcul estSolution2 doit renvoyer 1 si le nombre xTest appartient à l'ensemble des solutions. Voici la formule qu'il doit contenir :
si(sup,si(apos,si(racpos,solution1(xTest),solution2(xTest)),si(racpos,solution3(xTest),solution4(xTest))),si(apos,si(racpos,solution3(xTest),solution4(xTest)),si(racpos,solution1(xTest),solution2(xTest))))
Le calcul repContientSol2 contient comme formule repPourBornes2(-eps)&repPourBornes2(1+eps)&repPourBornes2(2-eps). Il doit rendre la valeur 1 si chacun des nombres situé à eps près des bornes des intervalles solutions et dans l'ensemble des solutions vérifie la fonction repPourBornes (dont la formule est fournie par LaboMep).
Remplacez sa formule par :
si(sup&apos|inf&aneg,si(racpos,repPourBornes2(-eps)&repPourBornes2(x0+eps),repPourBornes2(x0-eps)&repPourBornes2(0+eps)),si(racpos,repPourBornes2(0+eps)&repPourBornes2(x0-eps),repPourBornes2(x0+eps)&repPourBornes2(-eps)))
Le calcul nommé resolu2 est très important : c'est lui qui permet de savoir s'il l'élève a bien donné la (ou les) réponses attendues comme réponses finales. Il doit prendre comme valeur 1 dans ce cas et 0 sinon.
Voici la formule qu'il doit contenir :
si(sup,si(apos,si(racpos,teq1,teq2),si(racpos,teq3,teq4)),si(apos,si(racpos,teq3,teq4),si(racpos,teq1,teq2)))
Le calcul nommé PresqueResolu2 contient actuellement comme formule teqsol22+0*prov.
Ce calcul doit valoir 1 si la réponse de l'élève dans laquelle toutes les bornes ouvertes ont été remplacés par des bornes fermées est équivalente à la bonne réponse avec des bornes partout fermées.
Remplacez sa formule par 0 car nous ne voulons pas donner d'indication en cas d'erreur sur les bornes dans la réponse de l'élève.
Vous pouvez maintenant supprimer les calculs ou fonctions nommés teqsol21, teqsol22, sol21, sol22 qui n'avaient été créés qu'à titre d'exemple par la macro construction et ne sont plus utilisés.
Remarque : Tout cela n'est pas simple mais permettra de vérifier si la réponse de l'élève est bonne, même si ce n'est pas la réponse finale attendue.
Imaginons que, par exemple l'intervalle solution est [0;5/3[. Les réponses suivantes seront alors acceptées comme exactes mais pas terminées :
- [0;10/6[
- [0;1[U[1;5/3[
- [0;1]U]1;10/6[
Si vous ne souhaitez pas une gestion fine de la réponse de l'élève comme ci-dessus alors ne gardez que les calculs nommés ici solution1, solution2, solution3, solution4, teq1, teq2, teq3, teq4 et resolu2 (ne nom de resolu2 est impératif, le 2 signifiant à l'étape 2, les autres noms peuvent être changés.
Complétons notre figure.
Utilisez l'outil ![]() (création de calcul réel) pour créer les quatre calculs suivants :
(création de calcul réel) pour créer les quatre calculs suivants :
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| cas1 | (sup&apos|inf&aneg)&racpos | vaut 1 quand l'ensemble des solutions est l'extérieur des racines et -b/a>0 et 0 sinon |
| cas2 | (sup&apos|inf&aneg)&racneg | vaut 1 quand l'ensemble des solutions est l'extérieur des racines et -b/a<0 et 0 sinon |
| cas3 | (sup&aneg|inf&apos)&racpos | vaut 1 quand l'ensemble des solutions est l'intérieur des racines et -b/a>0 et 0 sinon |
| cas4 | (sup&aneg|inf&apos)&racneg | vaut 1 quand l'ensemble des solutions est l'intérieur des racines et -b/a<0 et 0 sinon |
Nous devons aussi fournir un affichage LaTeX dont le code fournisse les lignes à afficher lors de la correction. Cet affichage LaTeX utilisera les quatre calculs cas1, cas2, cas3 et cas4 via des affichages LaTeX conditionnels pour afficher l'ensemble des solutions.
Cet affichage LaTeX a déjà été préparé quand nous avons implémenté la macro construction preparation2Etapes. Il peut être nécessaire de le daplacer vers le bas si son contenu est recouvert par les autres affichages LaTeX contenant l'énoncé et le formulaire. Vous pouvez le modifier dans la boîte de dialogue de protocole de la figure ou avec l'outil ![]() de modification d'objet graphique.
de modification d'objet graphique.
Mais auparavant il faut reclasser cet affichage LaTeX vers la fin des objets créés afin qu'il puisse utiliser les calculs que nous venons de définir.
Utilisez doc l'outil ![]() et cliquez sur cet affichage LaTeX. Il a maintenant été reclassé en fin des objets créés et nous pouvons modifier son code LaTeX comme nous le voulons.
et cliquez sur cet affichage LaTeX. Il a maintenant été reclassé en fin des objets créés et nous pouvons modifier son code LaTeX comme nous le voulons.
Utilisez l'icône ![]() et cliquez sur cet affichage LaTeX pour le modifier.
et cliquez sur cet affichage LaTeX pour le modifier.
Voici le code LaTeX à entrer à la place du code existant:
\begin{array}{l}
\text{A résoudre : $\ForSimp{f}\If{sup}{\ge}{\le}0$}
\\ \text{$u(x)=\ForSimp{u}$ est de la forme $ax+b$ avec $a=\Val{a}$ et $b=\Val{b}$.}
\\ \text{$u(x)=0 \Leftrightarrow \ForSimp{u}=0 \Leftrightarrow x=\ForSimp{x0}$.}
\\ \text{Quand $x$ est "à droite" de $\ForSimp{x0}$, $u(x)$ a le signe de $a=\Val{a}$ donc est ici \If{apos}{positif}{négatif}.}
\\ \text{Le quotient $\ForSimp{f}$ s'annule pour $x=0$ et n'existe pas pour $x=\ForSimp{x0}$, valeur pour laquelle son dénominateur s'annule.}
\\ \text{$\ForSimp{x0}$ n'est pas solution car le quotient n'est pas défini pour cette valeur et $0$ est solution car le quotient existe et est nul pour cette valeur et l'inégalité est large.}
\\ \text{On repère dans la dernière ligne du tableau le signe cherche (ici le signe \If{sup}{+}{-}) et on lit dans la première ligne l'ensemble des solutions (en rouge).}
\\ \text{L'ensemble des solutions est donc}
\\ \text{$S=
\If{cas1}
{
]-\infty;0] \cup ]\ForSimp{x0};+\infty[
}
{
\If{cas2}
{
]-\infty;\ForSimp{x0}[ \cup [0;+\infty[
}
{
\If{cas3}
{
[0;\ForSimp{x0}[
}
{
]\ForSimp{x0};0]
}
}
}
$}
\end{array}
Validez et utilisez ensuite l'outil protocole ![]() pour affecter à cet affichage LaTeX le tag solution.
pour affecter à cet affichage LaTeX le tag solution.
Utilisez maintenant l'outil gomme ![]() pour masquer tous les affichages LaTeX que nous avons créé sous le tableau des variations ainsi que les affichages LaTeX rouges du tableau de variations qui n'ont pas à rester visibles (utilisez l'outil
pour masquer tous les affichages LaTeX que nous avons créé sous le tableau des variations ainsi que les affichages LaTeX rouges du tableau de variations qui n'ont pas à rester visibles (utilisez l'outil ![]() d'exécution de macro pour passer à l'étape 1 et masquer l'énoncé à cette étape).
d'exécution de macro pour passer à l'étape 1 et masquer l'énoncé à cette étape).
Nous allons maintenant rajouter des éléments de correction sur le tableau de variations.
Ces éléments ne devront apparaître que lors de la correction. Pour cela nous allons créer une variable cor qui ne pourra prendre que deux valeurs 0 et 1, la valeur 1 étant réservée au mode correction.
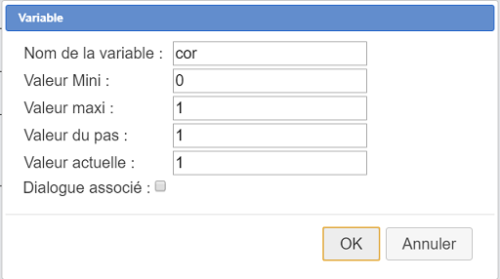
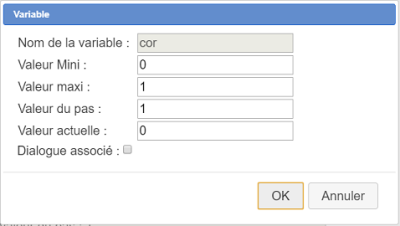
Déroulez la barre des calculs et activez l'outil ![]() de création d'une variable.
de création d'une variable.
Remplissez la boîte de dialogue comme ci-dessous :
Nous allons maintenant avoir besoin de deux autres constructions que vous pouvez télécharger ci-dessous :
Décompressez ce fichier zip dans le même dossier que précédemment et utilisez l'icône ![]() et l'item Incorporer une construction depuis un fichier pour incorporer les deux constructions qu'il contient dans votre figure (les fichiers constructions se nomment SegmentOuvert.mgc et SegmentSemiOuvert.mgc).
et l'item Incorporer une construction depuis un fichier pour incorporer les deux constructions qu'il contient dans votre figure (les fichiers constructions se nomment SegmentOuvert.mgc et SegmentSemiOuvert.mgc).
Ces deux macros permettent de créer un segment avec un ou deux petits crochets en forme de demi-cercle, le rayon de ces demi-cercles devant être donné en pixels.
Nous avons créé au début un calcul nommé raypix de formule 6 qui nous servira de rayon commun pour tous nos crochets en forme de demi-cercle.
Si nécessaire, la modification de ce calcul nous permettra de modifier les rayons de tous nos petits crochets.
Nous allons provisoirement modifier la formule du calcul cas1 pour qu'il soit égal à 1.
Utilisez l'outil ![]() de la barre supérieure (modification d'obejt numérique), sélectionnez cas1 dans la liste et remplacéez sa formule par :
de la barre supérieure (modification d'obejt numérique), sélectionnez cas1 dans la liste et remplacéez sa formule par :
1|(sup&apos|inf&aneg)&racpos
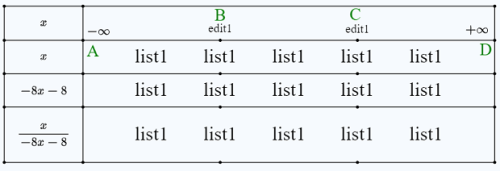
Pour plus de facilité nous allons utiliser les noms sur la figure ci-dessous : A, B, C et D.
Dans la palette des couleurs, activez la oouleur rose.
Déroulez la barre d'outil des transformations et cliquez sur l'icône ![]() (homothétie).
(homothétie).
Comme centre de l'homothétie, cliquez sur le point en haut et à gauche du tableau. Il vous est ensuite demandé le rapport de l'homothétie : entrez 1/(cor&cas1).
Cliquez ensuite sur le point B et sur le point C pour obtenir leurs images.
Activez l'icône ![]() (gestion des constructions) et choisissez l'item Implémenter une construction de la figure.
(gestion des constructions) et choisissez l'item Implémenter une construction de la figure.
Choisissez la construction SegmentSemiOuvert comme ci-dessous :
Une boîte de dialogue vous demande ensuite le choix de l'objet source n°1 qui est le rayon en pixel des crochets : sélectionnez le calcul raypix comme ici : 
Vous devez ensuite cliquer sur le point où le segment est fermé : cliquez sur B (il vous sera demandé de choisir entre deux points, il faut choisir le deuxième) puis sur le point où le segment est ouvert : cliquez sur A.
Le “segment” semi-ouvert généré apparaît.
Procédez de même et utilisez cette fois la construction nommée SegmentOuvert avec le rayon raypix puis en cliquant sur les points C et D.
Utilisez l'outil ![]() pour masquer les deux points roses.
pour masquer les deux points roses.
Le haut du tableau ressemble à ceci :
Maintenant utilisez l'outil ![]() pour remplacer la formule de cas1 par :
pour remplacer la formule de cas1 par :
0&(sup&apos|inf&aneg)&racpos
puis validez. Les objets précédemment créés disparaissent (car ils n'existe plus puisque cas1 vaut 0 et le rapport de l'homothétie n'existe plus).
Modifiez maintenant la formule de cas2 en : 1|(sup&apos|inf&aneg)&racneg
Procédez de même que précédemment en créant l'image des points B et C par une homothetie de rapport 1/(cor&cas2).
Utilisez la construction SegmentOuvert pour joindre B (en fait le deuxième point confondu avec B) et A.
Utilisez la construction SegmentSemiOuvert pour joindre les points C (en fait le deuxième point) et D.
Masquez les deux points images par homothétie et modifiez la formule de cas2 en : 0&(sup&apos|inf&aneg)&racneg
Modifiez maintenant la formule de cas3 en : 1|(sup&aneg|inf&apos)&racpos
Procédez de même que précédemment en créant l'image du point B par une homothetie de rapport 1/(cor&cas3).
Utilisez la construction SegmentSemiOuvert pour joindre le point B (en fait le deuxième point image) et C (commencer par B là ou le segment est fermé).
Masquez le point image par une homothetie.
Modifiez maintenant la formule de cas3 en : 0&(sup&aneg|inf&apos)&racpos
Ne reste plus que le quatrième cas.
Modifiez maintenant la formule de cas4 en : 1|(sup&aneg|inf&apos)&racneg
Créez l'image du point C par une homothétie de rapport 1/(cor&cas4).
Utilisez la construction SegmentSemiOuvert pour joindre le point C (en fait le deuxième point image) et B (commencer par C là ou le segment est fermé).
Masquez le point image par une homothetie.
Il faut maintenant réaffecter les formules initiales à cas1, cas2, cas3 et cas4 comme ci-dessous (il suffit de supprimer les deux premiers caractères de la formule).
| Nom du calcul | Formule |
|---|---|
| cas1 | (sup&apos|inf&aneg)&racpos |
| cas2 | (sup&apos|inf&aneg)&racneg |
| cas3 | (sup&aneg|inf&apos)&racpos |
| cas4 | (sup&aneg|inf&apos)&racneg |
Vous pouvez utiliser l'outil ![]() (recalcul de la figure) qui relance les tirages aléatoires pour voir si tout se passe bien dans la première ligne de notre tableau de variations.
(recalcul de la figure) qui relance les tirages aléatoires pour voir si tout se passe bien dans la première ligne de notre tableau de variations.
Utilisez l'outil ![]() (modification d'objet numérique) pour modifier la variable cor et lui donner comme valeur actuelle 0 comme ci-dessous puis validez.
(modification d'objet numérique) pour modifier la variable cor et lui donner comme valeur actuelle 0 comme ci-dessous puis validez.
Nos “segments” ouverts et semi-ouverts ne doivent plus être visibles.
Nous allons maintenant créer une macro qui sera exécutée lors de la correction de l'exercice.
Déroulez la barre d'outils des affichages et, à sa droite, cliquez sur l'icône ![]() (création d'une macro, à ne pas confondre avec les constructions).
(création d'une macro, à ne pas confondre avec les constructions).
Dans la liste proposée, choisissez l'item Macro d'affectation de valeur à variable.
Cliquez à un emplacement libre de la figure et remplissez la boîte de dialogue comme ci-dessous (il est impératif que son intitulé soit solution).
Cette macro affectera la valeur 1 à la variable cor ce qui rendra visible nos éléments de correction.
Utilisez l'outil ![]() pour masquer cette macro.
pour masquer cette macro.
Il nous reste pour la suite à connaître les dimensions de notre tableau.
Utilisez l'icône ![]() de la barre supérieure (options de la figure), cochez la case Utiliser un cadre de dimensions données puis validez.
de la barre supérieure (options de la figure), cochez la case Utiliser un cadre de dimensions données puis validez.
Un cadre grisé apparaît. il occupe toute la figure.
Avec l'outil de capture, capturez son coin en bas et à droite pour qu'il n'englobe que le tableau des variations comme ci-dessous :
Vous pouvez maintenant y lire les dimensions du cadre (ici 671 x 233). Il faut les noter car elles nous serviront lors de la création de la ressource (en arrondissant).
N'oubliez pas par précaution d'enregistrer votre figure.
Une remarque : une fois la figure finie on peut supprimer les macro constructions qu'elle contient pour la rendre plus légère. Il faut pour cela utiliser l'outil ![]() puis l'item Supprimer une construction de la figure.
puis l'item Supprimer une construction de la figure.
Etape 2 : Création de notre ressource dans LaboMep
Connectez vous à LaboMep avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).
Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez par exemple Inéquation quotient.
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez la case Seconde.
Dans les champs Résumé et Description, entrez Demande de résoudre une inéquation de la forme x/(ax+b) ≥ 0 ou x/(ax+b) ≤ 0.
En bas de la page, cliquez sur Créer la ressource.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour J3P.
Ensuite faites glisser Exercice de calcul multi-éditeurs et multi-étapes dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ Titre entrez ce qui suit :
Résoudre x/(ax+b) ≥ 0 ou x/(ax+b) ≤ 0
Dans le champ nbrepetitions entrez la valeur 2.
Ouvrez la figure principale depuis l'endroit où vous l'aviez sauvegardée et utilisez l'icône ![]() d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
Collez ce code Base 64 dans le champ fig après avoir cliqué sur le bouton Saisie brute.
Dans les champs width et height entrez respectivement 680 et 240 (nous utilisons les dimensions arrondies de notre tableau).
Dans le champ Param entrez ab (nous donnons à l'utilisateur la possibilité d'imposer les valeurs de a ou b).
Dans le champ nbEssais1 entrez 3 : l'élève aura 3 chances pour remplir correctement le tableau de signes (étape 1).
Dans le champ nbEssais2 entrez 2 : On laissera la possibilité à l'élève de se tromper une fois sur l'ensemble des solutions.
Dans le champ coefEtape1, entrez 0.6 (nous donnons un peu plus d'importance pour le score au tableau de signes). Il restera un coefficient de 0.4 pour la résolution de l'inéquation.
Dans le champ charset1, entrez : -\d.,/ (il s'agit des caractères au clavier permis lors de la première étape, \d pour tous les chiffres.)
Dans le champ charset2, entrez : \d+-*/()[]; (il s'agit des caractères clavier permis pour la deuxième étape, résolution de l'inéquation).
Cochez la case btnFrac (le bouton fraction) et décochez toutes les autres cases correspondants aux autres boutons.
Validez les autres paramètres tel quels.
Dans l'éditeur de graphe, cliquez droit sur le nœud principal et renommez-le x/(ax+b) ≥ 0 ou x/(ax+b) ≤ 0
Cliquez ensuite en bas sur le bouton Enregistrer pour sauvegarder votre ressource.
Vous pouvez maintenant tester votre ressource.
Si quelque chose ne fonctionne pas bien il faudra reprendre la figure MathGraph32, la corriger et modifier le paramètre fig de la figure.