Ceci est une ancienne révision du document !
Table des matières
Calcul de dérivée en deux étapes avec LaTeX dans une liste déroulante
Le but est de créer un exercice analogue à cet exercice :

Pour créer cette ressource vous devez utiliser la version JavaScript de MathGraph32, version 6.6.0 ou ultérieure, ou utiliser la version en ligne sur le site de MathGraph32.
Si nécessaire, à l'aide de l'icône ![]() de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
de la barre supérieure, mettez MathGraph32 en mode Avancé sans prise en charge des nombres complexes.
Nous voulons demander le calcul en plusieurs étapes de la dérivée de la fonction f définie soit par f(x)= (ax²+b)^n soit f(x) = √(ax²+b) où a et b sont deux entiers naturels strictement positifs et n un entier supérieur ou égal à 2.
Etape 1 : Création de la figure MathGraph
Commencez par créer la figure mathgraph.
Si vous désirez sauter ce qui suit vous pouvez utiliser le code Base 64 de la figure ci-dessous et, dans MathGraph32, utiliser l'icône ![]() puis choisir Figure par code Base 64.
puis choisir Figure par code Base 64.
TWF0aEdyYXBoSmF2YTEuMAAAABM+TMzNAAJmcv###wEA#wEAAAAAAAAAAAQPAAACjgAAAQEAAAAAAAAAAQAAADP#####AAAAAQAKQ0NhbGNDb25zdAD#####AAJwaQAWMy4xNDE1OTI2NTM1ODk3OTMyMzg0Nv####8AAAABAApDQ29uc3RhbnRlQAkh+1RELRj#####AAAAAQAHQ0NhbGN1bAD#####AAhuYkV0YXBlcwABMgAAAAFAAAAAAAAAAAAAAAIA#####wAFbmJ2YXIAATQAAAABQBAAAAAAAAAAAAACAP####8ABm5iY2FzMQABOAAAAAFAIAAAAAAAAAAAAAIA#####wAGbmJjYXMyAAE4AAAAAUAgAAAAAAAAAAAAAgD#####AAZuYmNhczMAATQAAAABQBAAAAAAAAAAAAACAP####8ABm5iY2FzNAABMgAAAAFAAAAAAAAAAAAAAAIA#####wACcjEAE2ludChyYW5kKDApKm5iY2FzMSn#####AAAAAgAJQ0ZvbmN0aW9uAv####8AAAABAApDT3BlcmF0aW9uAgAAAAMRAAAAAQAAAAAAAAAAP7YmJMQqGSD#####AAAAAQAPQ1Jlc3VsdGF0VmFsZXVyAAAAAwAAAAIA#####wACcjIAE2ludChyYW5kKDApKm5iY2FzMikAAAADAgAAAAQCAAAAAxEAAAABAAAAAAAAAAA#1For535MbAAAAAUAAAAEAAAAAgD#####AAJyMwATaW50KHJhbmQoMCkqbmJjYXMzKQAAAAMCAAAABAIAAAADEQAAAAEAAAAAAAAAAD+s6GOpsv4gAAAABQAAAAUAAAACAP####8AAnI0ABNpbnQocmFuZCgwKSpuYmNhczQpAAAAAwIAAAAEAgAAAAMRAAAAAQAAAAAAAAAAP7tiEUDMXeAAAAAFAAAABgAAAAIA#####wABYQAEcjErMQAAAAQAAAAABQAAAAcAAAABP#AAAAAAAAAAAAACAP####8AAWIABHIyKzEAAAAEAAAAAAUAAAAIAAAAAT#wAAAAAAAAAAAAAgD#####AAFuAARyMysyAAAABAAAAAAFAAAACQAAAAFAAAAAAAAAAAAAAAIA#####wABZgAEcjQrMQAAAAQAAAAABQAAAAoAAAABP#AAAAAAAAAAAAACAP####8AA2djZAAJcGdjZChhLGIp#####wAAAAEADUNGb25jdGlvbjJWYXICAAAABQAAAAsAAAAFAAAADAAAAAIA#####wACYScABWEvZ2NkAAAABAMAAAAFAAAACwAAAAUAAAAPAAAAAgD#####AAJiJwAFYi9nY2QAAAAEAwAAAAUAAAAMAAAABQAAAA8AAAACAP####8AAmYxAANmPTEAAAAECAAAAAUAAAAOAAAAAT#wAAAAAAAA#####wAAAAEABUNGb25jAP####8AAmcxAA0oYScqeF4yK2InKV5u#####wAAAAEACkNQdWlzc2FuY2UAAAAEAAAAAAQCAAAABQAAABAAAAAI#####wAAAAIAEUNWYXJpYWJsZUZvcm1lbGxlAAAAAAAAAAFAAAAAAAAAAAAAAAUAAAARAAAABQAAAA0AAXgAAAAHAP####8AAmcyAA9zcXJ0KGEnKnheMitiJykAAAADAQAAAAQAAAAABAIAAAAFAAAAEAAAAAgAAAAJAAAAAAAAAAFAAAAAAAAAAAAAAAUAAAARAAF4AAAABwD#####AAR6ZXJvABFhYnMoeCk8MC4wMDAwMDAwMQAAAAQEAAAAAwAAAAAJAAAAAAAAAAE+RXmO4jCMOgABeP####8AAAACAAZDTGF0ZXgA#####wAAAAABAAdlbm9uY2Ux#####xBANQAAAAAAAEA1rhR64UeuAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAEDXGJlZ2lue2FycmF5fXtsfQpcdGV4dHtPbiBkw6lzaXJlIGNhbGN1bGVyIGxhIGTDqXJpdsOpZSBkZSBsYSBmb25jdGlvbiAkZiQKIGTDqWZpbmllIHN1ciAkXFIkIHBhciAkZih4KT1cSWZ7ZjF9e1xGb3JTaW1we2cxfX17XEZvclNpbXB7ZzJ9fSQufQpcXCBcdGV4dHtMYSBkw6lyaXbDqWUgZG9pdCDDqnRyZSBkb25uw6llIHNvdXMgbGEgZm9ybWUgbGEgcGx1cyBzaW1wbGUKIGV0IGxhIHBsdXMgZmFjdG9yaXPDqWUgcG9zc2libGUufQpcZW5ke2FycmF5fQAAAAoA#####wAAAAABAAtmb3JtdWxhaXJlMf####8QQDUAAAAAAABAYPXCj1wo9gAAAAAAAAAAAAAAAAABAAAAAAAAAAAAZlxiZWdpbnthcnJheX17bH0KXHRleHR7TGEgZm9ybXVsZSDDoCBhcHBsaXF1ZXIgcG91ciBjYWxjdWxlciA8aT5mICcoeCk8L2k+IGVzdCBsaXN0MX0gClxcIApcZW5ke2FycmF5fQAAAAoA#####wAAAAABAAZsaXN0MTH#####EEB88AAAAAAAQFyrhR64UewAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAVZcYmVnaW57YXJyYXl9e2x9ClxJZntmMX0KewpcdGV4dHskXGxlZnQoIHhebiBccmlnaHQpJz1uIHhee24tMX0kfQpcXCBcdGV4dHskXGxlZnQoIHVebiBccmlnaHQpJz1uIHUnIHVee24tMX0kfQpcXCBcdGV4dHskXGxlZnQoIHVebiBccmlnaHQpJz1uIHVee24tMX0kfQp9CnsKXHRleHR7JFxsZWZ0KCBcc3FydHt1fSBccmlnaHQpJz1cZGZyYWN7dSd9e1xzcXJ0e3V9fSR9ClxcIFx0ZXh0eyRcbGVmdCggXHNxcnR7eH0gXHJpZ2h0KSc9XGRmcmFjezF9ezJcc3FydHt4fX0kfQpcXCBcdGV4dHskXGxlZnQoIFxzcXJ0e3V9IFxyaWdodCknPVxkZnJhY3t1J317MlxzcXJ0e3V9fSR9Cn0KXGVuZHthcnJheX0AAAACAP####8ACXJlc2xpc3QxMQAKc2koZjEsMiwzKf####8AAAABAA1DRm9uY3Rpb24zVmFyAAAAAAUAAAASAAAAAUAAAAAAAAAAAAAAAUAIAAAAAAAAAAAABwD#####AAF1AAdhKnheMitiAAAABAAAAAAEAgAAAAUAAAALAAAACAAAAAkAAAAAAAAAAUAAAAAAAAAAAAAABQAAAAwAAXgAAAAKAP####8AAAAAAQAHZW5vbmNlMv####8QQDcAAAAAAABAaPXCj1wo9gAAAAAAAAAAAAAAAAABAAAAAAAAAAABFVxiZWdpbnthcnJheX17bH0KXHRleHR7JGYoeCk9XElme2YxfXtcRm9yU2ltcHtnMX19e1xGb3JTaW1we2cyfX0kLiBFbiBwb3NhbnQgJHUoeCk9XEZvclNpbXB7dX0kIG9uIGEgJFxJZntmMX17Zj11XntcVmFse259fX17Zj1cc3FydHt1fX0kCiBldCA8aT5mICc8L2k+IFxJZntmMX17JD1udSd1XntuLTF9JCBhdmVjICRuPVxWYWx7bn0kfXskPVxkZnJhY3t1J317MlxzcXJ0e3V9fSR9fQpcXCBcdGV4dHtDYWxjdWxlciBtYWludGVuYW50IDxpPmYgJyh4KTwvaT4gOn0KXGVuZHthcnJheX0AAAAKAP####8AAAAAAQALZm9ybXVsYWlyZTL#####EEA5AAAAAAAAQHKa4UeuFHsAAAAAAAAAAAAAAAAAAQAAAAAAAAAAABxcdGV4dHs8aT5mICcoeCk8L2k+ID0gZWRpdDF9AAAAAgD#####AANuYTIABm4qYScqMgAAAAQCAAAABAIAAAAFAAAADQAAAAUAAAAQAAAAAUAAAAAAAAAAAAAAAgD#####AAJuJwADbi0xAAAABAEAAAAFAAAADQAAAAE#8AAAAAAAAAAAAAcA#####wAEc29sMQAUbmEyKngqKGEnKnheMitiJylebicAAAAEAgAAAAQCAAAABQAAAB0AAAAJAAAAAAAAAAgAAAAEAAAAAAQCAAAABQAAABAAAAAIAAAACQAAAAAAAAABQAAAAAAAAAAAAAAFAAAAEQAAAAUAAAAeAAF4AAAABwD#####AARzb2wyABRhJyp4L3NxcnQoYScqeF4yK2InKQAAAAQDAAAABAIAAAAFAAAAEAAAAAkAAAAAAAAAAwEAAAAEAAAAAAQCAAAABQAAABAAAAAIAAAACQAAAAAAAAABQAAAAAAAAAAAAAAFAAAAEQABeAAAAAcA#####wAFc29sJzIAIGEnKngqc3FydChhJyp4XjIrYicpLyhhJyp4XjIrYicpAAAABAMAAAAEAgAAAAQCAAAABQAAABAAAAAJAAAAAAAAAAMBAAAABAAAAAAEAgAAAAUAAAAQAAAACAAAAAkAAAAAAAAAAUAAAAAAAAAAAAAABQAAABEAAAAEAAAAAAQCAAAABQAAABAAAAAIAAAACQAAAAAAAAABQAAAAAAAAAAAAAAFAAAAEQABeAAAAAcA#####wAFcmVwMjEAATAAAAABAAAAAAAAAAAAAXj#####AAAAAwAQQ1Rlc3RFcXVpdmFsZW5jZQD#####AAR0ZXExAAAAHwAAACIBAAAAAAE#8AAAAAAAAAEAAAAMAP####8ABHRlcTIAAAAgAAAAIgEAAAAAAT#wAAAAAAAAAQAAAAwA#####wAFdGVxJzIAAAAhAAAAIgEAAAAAAT#wAAAAAAAAAQAAAAIA#####wAIcmVzb2x1MjEAFnNpKGYxLHRlcTEsdGVxMnx0ZXEnMikAAAALAAAAAAUAAAASAAAABQAAACMAAAAECwAAAAUAAAAkAAAABQAAACUAAAACAP####8AAngxAAkxK3JhbmQoMCkAAAAEAAAAAAE#8AAAAAAAAAAAAAMRAAAAAQAAAAAAAAAAP+EGt+dI5UgAAAACAP####8AAngyAAsxLjErcmFuZCgwKQAAAAQAAAAAAT#xmZmZmZmaAAAAAxEAAAABAAAAAAAAAAA#vs+XGzDh0AAAAAIA#####wACeDMACzEuMityYW5kKDApAAAABAAAAAABP#MzMzMzMzMAAAADEQAAAAEAAAAAAAAAAD#qPdRRxTB0AAAAAgD#####AAZleGFjdDEASnplcm8ocmVwMjEoeDEpLXNvbDEoeDEpKSZ6ZXJvKHJlcDIxKHgyKS1zb2wxKHgyKSkmemVybyhyZXAyMSh4Myktc29sMSh4MykpAAAABAoAAAAECv####8AAAABAA5DQXBwZWxGb25jdGlvbgAAABUAAAAEAQAAAA0AAAAiAAAABQAAACcAAAANAAAAHwAAAAUAAAAnAAAADQAAABUAAAAEAQAAAA0AAAAiAAAABQAAACgAAAANAAAAHwAAAAUAAAAoAAAADQAAABUAAAAEAQAAAA0AAAAiAAAABQAAACkAAAANAAAAHwAAAAUAAAApAAAAAgD#####AAZleGFjdDIASnplcm8ocmVwMjEoeDEpLXNvbDIoeDEpKSZ6ZXJvKHJlcDIxKHgyKS1zb2wyKHgyKSkmemVybyhyZXAyMSh4Myktc29sMih4MykpAAAABAoAAAAECgAAAA0AAAAVAAAABAEAAAANAAAAIgAAAAUAAAAnAAAADQAAACAAAAAFAAAAJwAAAA0AAAAVAAAABAEAAAANAAAAIgAAAAUAAAAoAAAADQAAACAAAAAFAAAAKAAAAA0AAAAVAAAABAEAAAANAAAAIgAAAAUAAAApAAAADQAAACAAAAAFAAAAKQAAAAIA#####wAHZXhhY3QyMQAUc2koZjEsZXhhY3QxLGV4YWN0MikAAAALAAAAAAUAAAASAAAABQAAACoAAAAFAAAAKwAAAAIA#####wACYTIABGEnKjIAAAAEAgAAAAUAAAAQAAAAAUAAAAAAAAAAAAAABwD#####AAN1JzEABmEnKjIqeAAAAAQCAAAABAIAAAAFAAAAEAAAAAFAAAAAAAAAAAAAAAkAAAAAAAF4AAAABwD#####AAN1JzIABGEyKngAAAAEAgAAAAUAAAAtAAAACQAAAAAAAXgAAAAHAP####8ABGZvcjEAGG4qYTIqeCooYScqeF4yK2InKV4obi0xKQAAAAQCAAAABAIAAAAEAgAAAAUAAAANAAAABQAAAC0AAAAJAAAAAAAAAAgAAAAEAAAAAAQCAAAABQAAABAAAAAIAAAACQAAAAAAAAABQAAAAAAAAAAAAAAFAAAAEQAAAAQBAAAABQAAAA0AAAABP#AAAAAAAAAAAXgAAAAHAP####8ABGZvcjIAGGEyKngvKDIqc3FydChhJyp4XjIrYicpKQAAAAQDAAAABAIAAAAFAAAALQAAAAkAAAAAAAAABAIAAAABQAAAAAAAAAAAAAADAQAAAAQAAAAABAIAAAAFAAAAEAAAAAgAAAAJAAAAAAAAAAFAAAAAAAAAAAAAAAUAAAARAAF4AAAACgD#####AAAAAAEACHNvbHV0aW9u#####xBAPgAAAAAAAEB1uuFHrhR7AAAAAAAAAAAAAAAAAAEAAAAAAAAAAAGqXGJlZ2lue2FycmF5fXtsfQpcdGV4dHskdSQgZXN0IGTDqXJpdmFibGUgc3VyICRcUiQgYXZlYyAkdScoeCk9XEZvclNpbXB7dScxfT1cRm9yU2ltcHt1JzJ9JH0gClxJZntmMX17fXtcXCBcdGV4dHskdSQgbmUgcHJlbmQgc3VyICRcUiQgcXVlIGRlcyB2YWxldXJzIHN0cmljdGVtZW50IHBvc2l0aXZlcy59fQpcXCBcdGV4dHskZiQgPSBcSWZ7ZjF9eyR1Xm4kfXskXHNxcnR7dX0kfSwgJGYkIGVzdCBkw6lyaXZhYmxlIHN1ciAkXFIkIGV0IDxpPmYgJzwvaT5cSWZ7ZjF9eyQ9bnUndV57bi0xfSQgYXZlYyAkbj1cVmFse259JH17JD1cZGZyYWN7dSd9ezJcc3FydHt1fX0kfX0KXFwgXHRleHR7JGYnKHgpPVxJZntmMX17XEZvclNpbXB7Zm9yMX09XEZvclNpbXB7c29sMX19e1xGb3JTaW1we2ZvcjJ9PVxGb3JTaW1we3NvbDJ9fSR9ClxlbmR7YXJyYXl9################
Sinon :
Les calculs suivants ont été créés :
| Nom du calcul | Formule |
|---|---|
| nbEtapes | 2 |
| nbvar | 4 |
| nbcas1 | 8 |
| nbcas2 | 8 |
| nbcas3 | 4 |
| nbcas4 | 2 |
| r1 | int(rand(0)*nbcas1) |
| r2 | int(rand(0)*nbcas2) |
| r3 | int(rand(0)*nbcas3) |
| r4 | int(rand(0)*nbcas4) |
Le calcul nbEtapes sert à indiquer que notre exercice se déroule en deux étapes.
La création des calculs suivant nbEtapes est indispensable pour que la ressource j3p associée donne lors des répétitions successives des valeurs à r1, r2, …, r4 toutes distinctes les unes des autres.
Par exemple il sera donné à r1 des valeurs distinctes successives comprises entre 0 et 7 lors des répétitions (car nbcas1 est égal à 8) et à r4 des valeurs distinctes successives comprises entre 0 et 1 (car nbcas4 est égal à 1).
Les formules que nous mettons dans r1, r2, …, r4 ne servent donc qu'à simuler les formules qui seront mises dans ces calculs lors des répétitions successives.
C'est notre figure elle-même qui devra spécifier le nombre d'étapes du calcul, ici 2 étapes.
Créez maintenant les calculs suivants qui serviront à définir la fonction à dériver:
| Nom du calcul | Formule | Commentaire |
|---|---|---|
| a | r1+1 | Sert à définir la fonction. Compris entre 1 et 8 |
| b | r2+1 | Sert à définir la fonction. Compris entre 1 et 8 |
| n | r3+2 | Exposant. Compris entre 2 et 7 |
| f | r4+1 | Contient 1 pour la première formule (puissance) et deux pour la seconde (racine carrée) |
| gcd | pgcd(a,b) | |
| a' | a/gcd | |
| b' | b/gcd | a' et b' sont premiers entre eux |
| f1 | f=1 | Vaut 1 quand f est égal à 1 et O sinon. Servira dans les affichages LaTeX conditionnels |
Utilisez l'icône ![]() pour créer les fonctions d'une variable réelles suivantes :
pour créer les fonctions d'une variable réelles suivantes :
| Nom de la fonction | Variable formelle | Formule | Commentaire |
|---|---|---|---|
| g1 | x | (a'*x^2+b')^n | Correspond à la première formule de fonction à dériver. |
| g2 | x | sqrt(a'*x^2+b') | Correspond à la deuxième formule de fonction à dériver. |
| zero | x | abs(x)<0.000000001 | La fonction zero servira à évaluer les réponses à 'epsilon près' |
Nous allons maintenant créer deux affichages LaTeX libres.
Le premier contiendra l'énoncé de la première question.
Utilisez pour cela l'outil ![]() , cliquez en haut et à gauche de la figure et remplissez dans la boîte de dialogue le code LateX par ce qui suit :
, cliquez en haut et à gauche de la figure et remplissez dans la boîte de dialogue le code LateX par ce qui suit :
\begin{array}{l}
\text{On désire calculer la dérivée de la fonction $f$ définie sur $\R$ par $f(x)=\If{f1}{\ForSimp{g1}}{\ForSimp{g2}}$.}
\\ \text{La dérivée doit être donnée sous la forme la plus simple et la plus factorisée possible.}
\end{array}
Ce premier affichage Latex est un tableau dont chacune des lignes est de la forme \text{} dont le contenu est ce qui sera envoyé comme ligne de la consigne à afficher.
Il faut comprendre que lorsque les lignes de la consigne sont affichées dans la ressource, on est par défaut en mode texte et que ce qui est contenu entre des $ est lui en mode maths comme par exemple le f de la première ligne qui sera donc écrit en italiques.
Cet affichage LaTeX utilise un affichage conditionnel \If (spécifique à MathGraph32). Ainsi si le calcul f1 vaut 1 (c'est à dire si f = 1), ce sera la formule de g1 qui sera affichée et sinon ce sera celle de g2. Ces formules sont affichées via \ForSimp qui est aussi spécifique à MathGraph32 et provoque un affichage simplifié de la formule (par exemple les multiplications par 1 ne sont pas affichées).
Utilisez l'outil (protocole, déroulez la liste jusqu'au dernier objet (qui est notre affichage LaTeX), cliquez sur le bouton Changer le tag et entrez comme tag consigne1.
Fermez la boîte de protocole.
Réactivez l'outil l'outil , cliquez au-dessous de l'affichage LaTeX précédent et créez un affichage LaTeX dont le code LaTeX est le suivant :
\begin{array}{l}
\text{La formule à appliquer pour calculer <i>f '(x)</i> est list1}
\\
\end{array}
Ce formulaire sera donc affiché sur une seule ligne.
Il contient un seul champ d'édition qui sera une liste déroulante repérée dans le formulaire par lis1.
Utilisez de nouveau l'outil ![]() et affectez à ce dernier affichage LaTeX le tag formulaire1.
et affectez à ce dernier affichage LaTeX le tag formulaire1.
Il nous faut maintenant définir les items que proposera cette liste déroulante.
Cela se fait via la création d'un autre affichage LaTeX.
Utilisez à nouveau l'outil ![]() , cliquez en haut et à droite de la figure et remplissez dans la boîte de dialogue le code LateX par ce qui suit :
, cliquez en haut et à droite de la figure et remplissez dans la boîte de dialogue le code LateX par ce qui suit :
\begin{array}{l}
\If{f1}
{
\text{$\left( x^n \right)'=n x^{n-1}$}
\\ \text{$\left( u^n \right)'=n u' u^{n-1}$}
\\ \text{$\left( u^n \right)'=n u^{n-1}$}
}
{
\text{$\left( \sqrt{u} \right)'=\dfrac{u'}{\sqrt{u}}$}
\\ \text{$\left( \sqrt{x} \right)'=\dfrac{1}{2\sqrt{x}}$}
\\ \text{$\left( \sqrt{u} \right)'=\dfrac{u'}{2\sqrt{u}}$}
}
\end{array}
Là aussi nous utilisons un affichage conditionnel.
Cet affichage LaTeX rend un tableau de trois lignes dont chaque ligne est formée d'un \text{}. C'est le contenu de ces \text{} qui sera utilisé comme contenu de chaque item de la liste déroulante.
Ici ce contenu est encadré de $ : nous passons donc en mode maths ce qui nous permet d'utiliser des formules LaTeX et ces formules seront affichées comme de vraies formules de mathématiques par la liste déroulante. Si le contenu du \text{} n'était pas encadré par des $, le contenu serait affiché en mode texte.
Utilisez de nouveau l'outil ![]() et affectez à ce dernier affichage LaTeX le tag list11. Le premier chiffre est 1 car nous sommes dans la première étape et le second est 1 car c'est la première (et ici unique) liste déroulante du formulaire n° 1 (formulaire de la première question).
et affectez à ce dernier affichage LaTeX le tag list11. Le premier chiffre est 1 car nous sommes dans la première étape et le second est 1 car c'est la première (et ici unique) liste déroulante du formulaire n° 1 (formulaire de la première question).
Nous allons maintenant créer un calcul nommé reslist11 dont le rôle est d'indiquer quelle est la bonne réponse dans notre liste déroulante.
Utilisez donc l'icône ![]() pour créer un calcul nommé reslist11 avec comme formule :
pour créer un calcul nommé reslist11 avec comme formule :
si(f1,2,3)
En effet, si f vaut 1, c'est le deuxième item qui donne la bonne réponse et si f vaut 2 c'est le troisième.
Lorsque l'élève a répondu (bon ou faux) à la première question, nous devons afficher une suite dénoncé qui reprend le résultat de la première question et pose la question suivante. Cet énoncé est donné via un autre affichage LaTeX de la figure de tag enonce2.
Avant de le créer, créez avec l'outil ![]() une fonction numérique nommée u de la variable x avec comme formule :
une fonction numérique nommée u de la variable x avec comme formule :
a*x^2+b
Utilisez l'outil ![]() pour créer un nouvel affichage LaTeX libre au-dessous des précédents avec comme code LaTeX :
pour créer un nouvel affichage LaTeX libre au-dessous des précédents avec comme code LaTeX :
\begin{array}{l}
\text{$f(x)=\If{f1}{\ForSimp{g1}}{\ForSimp{g2}}$. En posant $u(x)=\ForSimp{u}$ on a $\If{f1}{f=u^{\Val{n}}}{f=\sqrt{u}}$
et <i>f '</i> \If{f1}{$=nu'u^{n-1}$ avec $n=\Val{n}$}{$=\dfrac{u'}{2\sqrt{u}}$}}
\\ \text{Calculer maintenant <i>f '(x)</i> :}
\end{array}
Utilisez l'outil ![]() et affectez à ce dernier affichage LaTeX le tag enonce2.
et affectez à ce dernier affichage LaTeX le tag enonce2.
Créons maintenant un affichage LaTeX donnant le formulaire à remplir pour la question 2.
Utilisez de nouveau l'icône ![]() pour créer un affichage LaTeX libre au-dessous des précédents avec le code LaTeX suivant :
pour créer un affichage LaTeX libre au-dessous des précédents avec le code LaTeX suivant :
\text{<i>f '(x)</i> = edit1}
Cet affichage contiendra un éditeur de formule qui est repéré dans la formulaire par les caractères edit1 (1 car c'est le premier et dernier éditeur du formulaire).
Vous remarquerez qu'ici nous avons utilisé une balise html <i> pour un meilleur rendu du f'. Ce n'est pas indispensable mais montre qu'en mode texte on peut utiliser des balises html de base. Elle ne sont pas bien rendues dans la figure MathGraph32 mais le seront dans l'exercice.
Utilisez l'outil ![]() et affectez à ce dernier affichage LaTeX le tag formulaire2.
et affectez à ce dernier affichage LaTeX le tag formulaire2.
Nous allons maintenant créer des objets numériques qui serviront à valider la réponse de l'élève dans le formulaire 2.
Utilisez l'outil ![]() pour créer les deux calculs réels suivants :
pour créer les deux calculs réels suivants :
| Nom du calcul | Formule |
|---|---|
| na2 | n*a'*2 |
| n' | n-1 |
Et maintenant l'outil ![]() pour créer les deux fonctions réelles suivantes
pour créer les deux fonctions réelles suivantes
| Nom de la fonction | Variable formelle | Formule | Explications |
|---|---|---|---|
| sol1 | x | na2*x*(a'*x^2+b')^n' | Correspond à la formule attendue comme réponse finale pour la dérivée de g1 |
| sol2 | x | a'*x/sqrt(a'*x^2+b') | Correspond à la première formule attendue comme réponse finale pour la dérivée de g2 |
| sol'2 | x | a'*x*sqrt(a'*x^2+b')/(a'*x^2+b') | Correspond à la deuxième formule attendue comme réponse finale pour la dérivée de g2 |
| rep21 | x | 0 | Sert à contenir la réponse de l'élève dans le champ d'édition n°1 du formulaire n°2 |
Nous allons maintenant créer trois test d'équivalence en déroulant la barre d'outils des calculs, en cliquant sur l'icône ![]() puis en choisissant Test d'équivalence dans la liste proposée.
puis en choisissant Test d'équivalence dans la liste proposée.
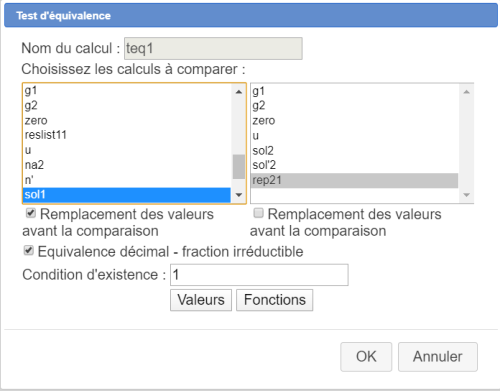
Remplissez la première boîte de dialogue comme ci-dessous pour créer le premier nommé teq1 :
Ce test d'équivalence vaudra 1 si, après simplifications, la formule contenue dans sol1 est équivalente algébriquement à celle contenue dans rep21.
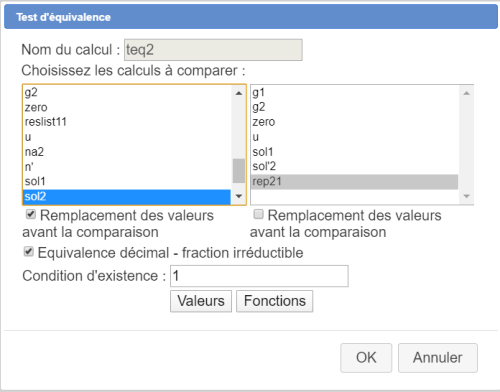
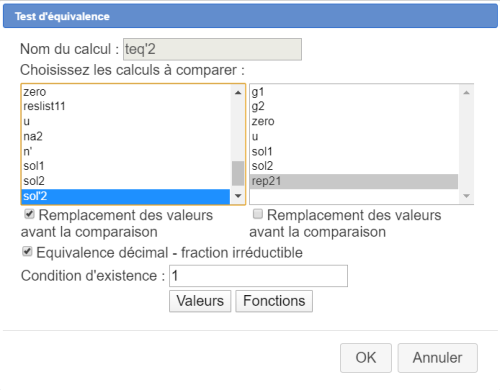
Créez de même deux autres tests d'équivalence nommés teq2 et teq'2 comme ci-dessous :
Maintenant créez les calculs réels suivants (outil ![]() :
:
| Nom du calcul | Formule | Explications | |
|---|---|---|---|
| resolu21 | si(f1,teq1,teq2 | teq'2) | C'est ce calcul qui permet à la ressource de savoir si l'élève a rendu une réponse finale valide dans l'éditeur n°1 du formulaire n°2 |
| x1 | 1+rand(0) | Sert à vérifier de façon approchée la réponse de l'élève | |
| x2 | 1.1+rand(0) | Sert à vérifier de façon approchée la réponse de l'élève | |
| x3 | 1.2+rand(0) | Sert à vérifier de façon approchée la réponse de l'élève | |
| exact1 | zero(rep21(x1)-sol1(x1))&zero(rep21(x2)-sol1(x2))&zero(rep21(x3)-sol1(x3)) | Vaut 1 si on peut considérer la réponse de l'élève comme exacte pour la solution sol1 | |
| exact2 | zero(rep21(x1)-sol1(x1))&zero(rep21(x2)-sol1(x2))&zero(rep21(x3)-sol1(x3)) | Vaut 1 si on peut considérer la réponse de l'élève comme exacte pour la solution sol1 | |
| exact21 | si(f1,exact1,exact2) | C'est ce calcul qui permet à la ressource de savoir si l'élève a rendu une réponse finale exacte dans l'éditeur n°1 du formulaire n°2 | |
| a2 | a'*2 | Servira dans le LaTeX de correction |
Créons maintenant des fonctions réelles de la variable réelle x qui serviront dans l'affichage de la correction :
| Fonction | Variable formelle | Formule |
|---|---|---|
| u'1 | x | a'*2*x |
| u'2 | x | a2*x |
| for1 | x | n*a2*x*(a'*x^2+b')^(n-1) |
| for2 | x | a2*x/(2*sqrt(a'*x^2+b')) |
Il nous reste à créer un affichage LaTeX dont le tag sera solution qui sera chargé d'afficher la correction de l'exercice.
Il serait possible de faire afficher cette correction dans la figure elle-même mais nous n'allons pas afficher cette figure (elle ne nous servira qu'à préparer les éléments de l'exercice)<.
Utilisez l'icône ![]() pour créer ce dernier affichage LaTeX au-dessous des précédents (l'emplacement importe peu). Entrez le code LaTeX suivant :
pour créer ce dernier affichage LaTeX au-dessous des précédents (l'emplacement importe peu). Entrez le code LaTeX suivant :
\begin{array}{l}
\text{$u$ est dérivable sur $\R$ avec $u'(x)=\ForSimp{u'1}=\ForSimp{u'2}$}
\If{f1}{}{\\ \text{$u$ ne prend sur $\R$ que des valeurs strictement positives.}}
\\ \text{$f$ = \If{f1}{$u^n$}{$\sqrt{u}$}, $f$ est dérivable sur $\R$ et <i>f '</i>\If{f1}{$=nu'u^{n-1}$ avec $n=\Val{n}$}{$=\dfrac{u'}{2\sqrt{u}}$}}
\\ \text{$f'(x)=\If{f1}{\ForSimp{for1}=\ForSimp{sol1}}{\ForSimp{for2}=\ForSimp{sol2}}$}
\end{array}
Utilisez l'outil ![]() pur affecter à ce dernier affichage LaTeX le tac solution.
pur affecter à ce dernier affichage LaTeX le tac solution.
Notre figure est prête à être utilisée dans une ressource j3p.
Etape 2 : Création de notre ressource dans LaboMep V2.
Connectez vous à LaboMep V2 avec votre identifiant et votre mot de passe : https://labomep.sesamath.net/
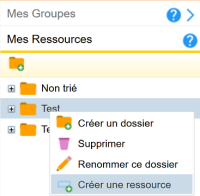
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).
Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez par exemple Calculer une dérivée.
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez la case terminale.
Dans les champs Résumé et Description, entrez Demande de calculer une dérivée après avoir demandé quelle formule utiliser.
En bas de la page, cliquez sur Créer la ressource.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour J3P.
Ensuite faites glisser Exercice de calcul multi-éditeurs et multi-étapes dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ Titre entrez ce qui suit :
Calculer une dérivée
Dans le champ nbrepetitions entrez la valeur 2.
Ouvrez la figure principale depuis l'endroit où vous l'aviez sauvegardée et utilisez l'icône ![]() d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
d'exportation de la barre d'outil supérieure pour coller dans le presse-papier le code Base 64 de la figure.
Collez ce code Base 64 dans le champ fig.
Il serait possible d'afficher sous les consignes notre figure MathGraph32 et dans ce cas nous devrions entrer la largeur et la hauteur en pixels comme paramètres width et height mais ici notre figure ne sert qu'à fournir ce qui sera affiché, aussi bien lors des questions que lors de la correction.
Nous allons donc entrer 0 comme paramètres width et height.
Dans le champ width entrez 0 (Largeur en pixels de la figure principale).
Dans le champ height entrez 0 (Hauteur en pixels de la figure principale).
Dans le champ param entrez abn ( ce sont les noms des calculs qui pourront être imposés lors de la personnalisation de notre ressource).
Dans le champ nbEssais1 entrez 1 (C'est le nombre d'essais maximum pour choisr la bonne formule de dérivée à l'étape 1).
Dans le champ nbEssais2 entrez par exemple 5 (C'est le nombre d'essais maximum pour calculer la dérivée à l'étape 2 deuxième étape).
Cochez la case true pour le paramètre listesLaTeX. C'est ce qui nous permet d'voir des formules dans notre liste déroulante.
Dans le champ charset2 entrez :
x0123456789,.()\^\+\-\*\/()²
Ce sont les caractères utilisables dans les champs d'édition à l'étape 2. Certains sont précédés d'un \ car il s'agit en fait d'une expression régulière. Quand vous avez un doute sur un caractère, préfixes-le d'un \.
Ce sont les caractères utilisables dans les champs d'édition à l'étape 3.
Dans le champ coefEtape1 entrez 0.5.
C'est ce qui sera affecté au score pour une bonne réponse à l'étape 1 (le score de l'exercice étant au maximum de 1). Le restant (1 - coefEtape1) sera réparti pour les réponses aux questions suivantes.
Si on entre comme valeur 0 pour coefEtape1, alors toutes les étapes se verront attribuer le même score.
Cochez les cases true pour btnFrac, btnRac, btnPuis et btnPrim pour avoir les boutons correspondant disponibles dans les éditeurs (farction, racine carrée et puissance) et décochez les autres.
Dans le champ InfoParam entrez :
Dérivée de rac(ax²+b) ou (ax²+b)^n, a et b (entiers strictement positifs premiers entre eux) et n entier, n > 1
Ainsi les utilisateurs de la ressource qui voudraient la personnaliser sauront quel est le rôle des paramètres a, b et n. Les autres ne servent pas.
Ici nous laissons tous ces paramètres à random pour qu'ils soient choisis aléatoirement comme nous l'avons prévu.
Vous pouvez maintenant valider la boîte de dialogue de choix des paramètres.
Ensuite cliquez en bas sur le bouton Enregistrer pour enregistrer votre ressource.
Si vous voulez maintenant tester votre ressource, fermez d’abord l’onglet Calculer une dérivée puis, dans Mes Ressources, faites un clic droit sur la ressource.
Vous pouvez maintenant tester la ressource.
Quelques compléments
Notre figure ne servait pas être affichée et c'est pourquoi nous avons mis les paramètres with et height à zéro.
Dans certains autres cas, la figure peut servir de support à la question et doit être affichée. RElle figure alors sous les consignes.
Il faut alors masquer tous les affichages LaTeX servant à donner énoncés, formulaire et correction.
Il est possible de déclencher le lancement d'une macro au début de chaque étape à partir de l'étape 2.
Ces macros doivent avoir pour intitulé macroEtape suivi du numéro de l'étape (2 ou plus).
Il est aussi possible d'utiliser un macro faisant apparaître des éléments de correction et d'afficher une autre figure d'explications lors de la phase de correction.
Pour ces fonctionnalités vous pouvez vous référer à ce tutoriel]
Il y a aussi des possibilités supplémentaires sur les listes déroulantes.
Si vous désirez par exemple que les items de la liste déroulante list11 soient mélangés au hasard quand ils sont présentés à l'élève, il suffit que votre figure contienne un calcul nommé listaleat11 valant 1.
Si vous désirez que plusieurs items de la liste list1 puissent être acceptés comme bons, votre figure doit contenir un calcul nommé repList11 qui doit être initialisé à une autre valeur que -1 (1 par exemple). C'est dans repList11 que le modèle mettra l'index de l'item qu'a choisi l'élève comme réponse.
Votre figure doit alors aussi contenir un autre calcul nommé exactList11 qui vaut 1 si la réponse qu'a choisie l'élève (que le modèle a mis dans repList1) est une des réponses acceptés comme exactes et 0 sinon.